Pythagoreisches Quadrupel

Ein pythagoreisches Quadrupel[1] ist ein Tupel von ganzen Zahlen ${\displaystyle a,b,c,d\in \mathbb {Z} }$, so dass gilt:

${\displaystyle a^{2}+b^{2}+c^{2}=d^{2}}$.

Alle vier primitiven pythagoreischen Quadrupel mit einstelligen Werten

Es handelt s​ich dabei u​m die Lösungen e​iner diophantischen Gleichung. Meistens werden a​ber nur positive g​anze Zahlen a​ls Lösungen betrachtet.[2]

Primitive pythagoreische Quadrupeln

Ein pythagoreisches Quadrupel ${\displaystyle (a,b,c,d)}$ heißt primitives pythagoreisches Quadrupel, wenn die Werte positiv ganzzahlig sind und der größte gemeinsame Teiler der vier Werte gleich 1 ist (wenn also ${\displaystyle \operatorname {ggT} (a,b,c,d)=1}$ gilt). Jedes pythagoreische Quadrupel ist ein ganzzahliges Vielfaches eines primitiven pythagoreischen Quadrupels.

Beispiel 1:

Das Tupel ${\displaystyle (a,b,c,d)=(2,3,6,7)}$ ist ein primitives pythagoreisches Quadrupel, weil ${\displaystyle \operatorname {ggT} (2,3,6,7)=1}$ ist und ${\displaystyle 2^{2}+3^{2}+6^{2}=7^{2}\quad (=49)}$ gilt.

Beispiel 2:

Das Tupel ${\displaystyle (a,b,c,d)=(5\cdot 2,5\cdot 3,5\cdot 6,5\cdot 7)=(10,15,30,35)}$ ist kein primitives pythagoreisches Quadrupel, weil ${\displaystyle \operatorname {ggT} (10,15,30,35)=5\not =1}$ ist, obwohl ${\displaystyle 10^{2}+15^{2}+30^{2}=35^{2}\quad (=1225)}$ gilt.

Beispiele

Es g​ibt 31 primitive pythagoreische Quadrupel, b​ei denen a​lle Werte kleiner a​ls 30 sind:

${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle d}$ ${\displaystyle a^{2}+b^{2}+c^{2}=d^{2}}$ 1 2 2 3 ${\displaystyle 1^{2}+2^{2}+2^{2}=3^{2}}$ 2 3 6 7 ${\displaystyle 2^{2}+3^{2}+6^{2}=7^{2}}$ 1 4 8 9 ${\displaystyle 1^{2}+4^{2}+8^{2}=9^{2}}$ 4 4 7 9 ${\displaystyle 4^{2}+4^{2}+7^{2}=9^{2}}$ 2 6 9 11 ${\displaystyle 2^{2}+6^{2}+9^{2}=11^{2}}$ 6 6 7 11 ${\displaystyle 6^{2}+6^{2}+7^{2}=11^{2}}$ 3 4 12 13 ${\displaystyle 3^{2}+4^{2}+12^{2}=13^{2}}$ 2 5 14 15 ${\displaystyle 2^{2}+5^{2}+14^{2}=15^{2}}$

${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle d}$ ${\displaystyle a^{2}+b^{2}+c^{2}=d^{2}}$ 2 10 11 15 ${\displaystyle 2^{2}+10^{2}+11^{2}=15^{2}}$ 1 12 12 17 ${\displaystyle 1^{2}+12^{2}+12^{2}=17^{2}}$ 8 9 12 17 ${\displaystyle 8^{2}+9^{2}+12^{2}=17^{2}}$ 1 6 18 19 ${\displaystyle 1^{2}+6^{2}+18^{2}=19^{2}}$ 6 6 17 19 ${\displaystyle 6^{2}+6^{2}+17^{2}=19^{2}}$ 6 10 15 19 ${\displaystyle 6^{2}+10^{2}+15^{2}=19^{2}}$ 4 5 20 21 ${\displaystyle 4^{2}+5^{2}+20^{2}=21^{2}}$ 4 8 19 21 ${\displaystyle 4^{2}+8^{2}+19^{2}=21^{2}}$

${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle d}$ ${\displaystyle a^{2}+b^{2}+c^{2}=d^{2}}$ 4 13 16 21 ${\displaystyle 4^{2}+13^{2}+16^{2}=21^{2}}$ 8 11 16 21 ${\displaystyle 8^{2}+11^{2}+16^{2}=21^{2}}$ 3 6 22 23 ${\displaystyle 3^{2}+6^{2}+22^{2}=23^{2}}$ 3 14 18 23 ${\displaystyle 3^{2}+14^{2}+18^{2}=23^{2}}$ 6 13 18 23 ${\displaystyle 6^{2}+13^{2}+18^{2}=23^{2}}$ 9 12 20 25 ${\displaystyle 9^{2}+12^{2}+20^{2}=25^{2}}$ 12 15 16 25 ${\displaystyle 12^{2}+15^{2}+16^{2}=25^{2}}$ 2 7 26 27 ${\displaystyle 2^{2}+7^{2}+26^{2}=27^{2}}$

${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle d}$ ${\displaystyle a^{2}+b^{2}+c^{2}=d^{2}}$ 2 10 25 27 ${\displaystyle 2^{2}+10^{2}+25^{2}=27^{2}}$ 2 14 23 27 ${\displaystyle 2^{2}+14^{2}+23^{2}=27^{2}}$ 7 14 22 27 ${\displaystyle 7^{2}+14^{2}+22^{2}=27^{2}}$ 10 10 23 27 ${\displaystyle 10^{2}+10^{2}+23^{2}=27^{2}}$ 3 16 24 29 ${\displaystyle 3^{2}+16^{2}+24^{2}=29^{2}}$ 11 12 24 29 ${\displaystyle 11^{2}+12^{2}+24^{2}=29^{2}}$ 12 16 21 29 ${\displaystyle 12^{2}+16^{2}+21^{2}=29^{2}}$

Aus diesen primitiven pythagoreischen Quadrupeln kann man beliebig viele weitere nicht-primitive pythagoreische Quadrupel bilden. Zum Beispiel kann man aus dem primitiven pythagoreischen Quadrupel ${\displaystyle (a,b,c,d)=(1,2,2,3)}$ durch Multiplikation mit ${\displaystyle 2,3,4,\ldots }$ die nicht-primitiven pythagoreischen Quadrupel ${\displaystyle (a,b,c,d)=(2,4,4,6)}$, ${\displaystyle (a,b,c,d)=(3,6,6,9)}$, ${\displaystyle (a,b,c,d)=(4,8,8,12)}$ etc. bilden.

Geometrische Deutung

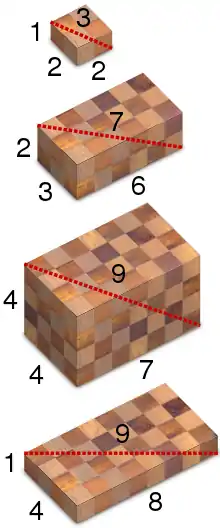
Ein pythagoreisches Quadrupel ${\displaystyle (a,b,c,d)}$ definiert einen Quader mit ganzzahligen Seitenlängen ${\displaystyle |a|,|b|}$ und ${\displaystyle |c|}$ (wobei mit ${\displaystyle |a|}$ der Betrag von ${\displaystyle a}$ gemeint ist). Die Raumdiagonale dieses Quaders hat dann eine ganzzahlige Länge ${\displaystyle |d|}$. Pythagoreische Quadrupel heißen deswegen auf englisch auch Pythagorean boxes.[3]

Eigenschaften von pythagoreischen Quadrupeln

• Das pythagoreische Quadrupel mit dem kleinsten Produkt ist ${\displaystyle (1,2,2,3)}$.
• Sei ${\displaystyle a^{2}+b^{2}+c^{2}=d^{2}}$ mit ${\displaystyle a,b,c,d\in \mathbb {N} }$. Dann gilt:[4]

Das Produkt ${\displaystyle abcd}$ ist immer durch ${\displaystyle 12}$ teilbar.

Eine größere Zahl, die dieses Produkt teilt, gibt es nicht, denn für das kleinste pythagoreische Quadrupel (also für ${\displaystyle (a,b,c,d)=(1,2,2,3)}$) gilt ${\displaystyle 1\cdot 2\cdot 2\cdot 3=12}$. Somit kann es keine größere Zahl geben, die das Produkt teilt.

Erzeugung von pythagoreischen Quadrupeln

• Methode 1:[2][5]

Seien ${\displaystyle (m,n,p,q)}$ positive ganze Zahlen. Dann kann die Menge der pythagoreischen Quadrupel mit ungeradem ${\displaystyle a}$ wie folgt erzeugt werden:

${\displaystyle {\begin{aligned}a&=m^{2}+n^{2}-p^{2}-q^{2},\\b&=2(mq+np),\\c&=2(nq-mp),\\d&=m^{2}+n^{2}+p^{2}+q^{2}\end{aligned}}}$

Gelten zusätzlich die folgenden elf Bedingungen, dann kann damit die Menge von primitiven pythagoreischen Quadrupeln mit ungeradem ${\displaystyle a}$ erzeugt werden.[6]

${\displaystyle {\begin{array}{lll}nq>mp,&&m^{2}+n^{2}>p^{2}+q^{2},\\m\geq 0,\;n\geq 1,\;p\geq 0,\;q\geq 1,&&m+p\geq 1,\\m+n+p+q\equiv 1{\pmod {2}},&&{\text{ das heißt, }}m+n+p+q{\text{ ist ungerade (also muss ein Wert oder müssen drei Werte gerade Zahlen sein)}}\\ggT(m^{2}+n^{2},p^{2}+q^{2},mq+np)=1,&&\\m=0\;\Longrightarrow \;q\leq p,&&p=0\;\Longrightarrow \;n\leq m\end{array}}}$

Alle primitiven pythagoreischen Quadrupel erfüllen somit die diophantische Gleichung ${\displaystyle d^{2}=a^{2}+b^{2}+c^{2}}$, welche man auch Lebesguesche Identität nennt:[7][8]

${\displaystyle (m^{2}+n^{2}+p^{2}+q^{2})^{2}=(m^{2}+n^{2}-p^{2}-q^{2})^{2}+(2mq+2np)^{2}+(2nq-2mp)^{2}}$

Beispiel 1:

Sei ${\displaystyle m:=1,n:=7,p:=2}$ und ${\displaystyle q:=5}$. Dann sind alle zusätzlichen Bedingungen erfüllt und es ist ${\displaystyle a=21,b=38,c=66}$ und ${\displaystyle d=79}$ und tatsächlich ist ${\displaystyle a^{2}+b^{2}+c^{2}=21^{2}+38^{2}+66^{2}=79^{2}=d^{2}\quad (=6241)}$ ein primitives pythagoreisches Quadrupel.

Beispiel 2:

Sei ${\displaystyle m:=2,n:=3,p:=5}$ und ${\displaystyle q:=9}$. Dann ist die zusätzliche Bedingung ${\displaystyle m^{2}+n^{2}=13{\stackrel {!}{>}}106=p^{2}+q^{2}}$ zwar nicht erfüllt, es ist aber ${\displaystyle a=-93,b=66,c=34}$ und ${\displaystyle d=119}$ wegen ${\displaystyle a^{2}+b^{2}+c^{2}=(-93)^{2}+66^{2}+34^{2}=119^{2}=d^{2}\quad (=14161)}$ trotzdem ein pythagoreisches Quadrupel, allerdings mit ${\displaystyle a=-93<0}$.

Beispiel 3:

Sei ${\displaystyle m:=1,n:=3,p:=1}$ und ${\displaystyle q:=2}$. Dann ist ${\displaystyle a=5,b=10,c=10}$ und ${\displaystyle d=15}$ und tatsächlich ist ${\displaystyle a^{2}+b^{2}+c^{2}=5^{2}+10^{2}+10^{2}=15^{2}=d^{2}\quad (=225)}$. Allerdings ist dieses pythagoreische Quadrupel nicht primitiv, weil ${\displaystyle \operatorname {ggT} (a,b,c,d)=5\not =1}$ und die Bedingung ${\displaystyle \operatorname {ggT} (m^{2}+n^{2},p^{2}+q^{2},mq+np)=5\not =1}$ ist.

• Methode 2:

Alle pythagoreischen Quadrupel (inklusive der nicht-primitiven) können wie folgt aus zwei positiven ganzen Zahlen ${\displaystyle a}$ und ${\displaystyle b}$ erzeugt werden:

Sei die Parität von ${\displaystyle a}$ und ${\displaystyle b}$ verschieden (sei also entweder ${\displaystyle a}$ gerade und ${\displaystyle b}$ ungerade oder ${\displaystyle a}$ ungerade und ${\displaystyle b}$ gerade). Sei weiters ${\displaystyle p}$ ein Faktor von ${\displaystyle a^{2}+b^{2}}$ mit ${\displaystyle p^{2}<a^{2}+b^{2}}$. Dann gilt:

${\displaystyle c={\frac {a^{2}+b^{2}-p^{2}}{2p}}}$ und ${\displaystyle d={\frac {a^{2}+b^{2}+p^{2}}{2p}}}$ mit ${\displaystyle p=d-c}$

Beispiel:

Sei ${\displaystyle a:=2,b:=11}$ und ${\displaystyle p:=5}$. Dann sind alle Voraussetzungen erfüllt und es ist ${\displaystyle c=10}$ und ${\displaystyle d=15}$ (und es ist ${\displaystyle p=d-c}$) und tatsächlich ist ${\displaystyle a^{2}+b^{2}+c^{2}=2^{2}+11^{2}+10^{2}=15^{2}=d^{2}\quad (=225)}$.

• Methode 3:[9]

Seien ${\displaystyle a}$ und ${\displaystyle b}$ beide gerade Zahlen. Seien außerdem ${\displaystyle l={\frac {a}{2}}}$, ${\displaystyle m={\frac {b}{2}}}$ und ${\displaystyle n}$ ein Faktor von ${\displaystyle l^{2}+m^{2}}$ mit ${\displaystyle n^{2}<l^{2}+m^{2}}$. Dann gilt:

${\displaystyle c={\frac {l^{2}+m^{2}-n^{2}}{n}}}$ und ${\displaystyle d={\frac {l^{2}+m^{2}+n^{2}}{n}}}$

Diese Methode erzeugt alle pythagoreischen Quadrupel exakt ein Mal, wenn ${\displaystyle l}$ und ${\displaystyle m}$ alle Paare natürlicher Zahlen durchlaufen und ${\displaystyle n}$ alle möglichen Werte für jedes Paar durchläuft.

Beispiel:

Sei ${\displaystyle a:=14,b:=6}$ und ${\displaystyle n:=2}$. Dann sind alle Voraussetzungen erfüllt, ${\displaystyle l=7}$, ${\displaystyle m=3}$ und es ist ${\displaystyle c=27}$ und ${\displaystyle d=31}$ und tatsächlich ist ${\displaystyle a^{2}+b^{2}+c^{2}=14^{2}+6^{2}+27^{2}=31^{2}=d^{2}\quad (=961)}$.

• Es gibt kein pythagoreisches Quadrupel, bei dem mehr als eine der Zahlen ${\displaystyle a}$, ${\displaystyle b}$, ${\displaystyle c}$ ungerade ist.

• Methode 4:

Sei ${\displaystyle n}$ eine positive ganze Zahl. Dann kann ein pythagoreisches Quadrupel wie folgt erzeugt werden:

${\displaystyle {\begin{aligned}a&=n,\\b&=n+1,\\c&=ab,\\d&=c+1\end{aligned}}}$

Beispiel:

Sei ${\displaystyle n=a=3}$, ${\displaystyle b=4}$ und ${\displaystyle c=12}$. dann ist ${\displaystyle d=13}$, und tatsächlich ist ${\displaystyle a^{2}+b^{2}+c^{2}=3^{2}+4^{2}+12^{2}=13^{2}=d^{2}\quad (=169)}$.

Siehe auch

• Pythagoreisches Tripel
• Drei-Quadrate-Satz

Weblinks

• Robert D. Carmichael: Diophantine Analysis. Mathematical Monographs, 1915, S. 1–100, abgerufen am 18. Oktober 2019.
• Eric W. Weisstein: Pythagorean Quadruple. Wolfram MathWorld, abgerufen am 18. Oktober 2019.

Einzelnachweise

1. Zur Schreibweise: Im aktuellen Duden – Das große Wörterbuch der deutschen Sprache in zehn Bänden - ISBN 3-411-70360-1 wird das Adjektiv „pythagoreisch“ in dieser Schreibweise gegeben und die Schreibweise „pythagoräisch“ als österreichische Sonderform bezeichnet.
2. Robert Spira: The Diophantine Equation x²+y²+z²=m². The American Mathematical Monthly 69 (5), 1962, S. 360–365, abgerufen am 11. Oktober 2019.
3. Raymond A. Beauregard, E. R. Suryanarayan: Pythagorean Boxes. Mathematics Magazine 74 (3), Juni 2001, S. 222–227, abgerufen am 11. Oktober 2019.
4. Des MacHale, Christian van den Bosch: Generalising a result about Pythagorean triples. The Mathematical Gazette 96 (535), März 2012, S. 91–96, abgerufen am 11. Oktober 2019.
5. Paul Oliverio: Self-Generating Pythagorean Quadruples and n-Tuples. Jefferson High School, Los Angeles, Dezember 1993, S. 98–101, abgerufen am 18. Oktober 2019.
6. Robert Spira: The Diophantine Equation x²+y²+z²=m², Theorem 2. The American Mathematical Monthly 69 (5), 1962, S. 362, abgerufen am 11. Oktober 2019.
7. Pythagorean Quadruple. GeeksforGeeks - A computer science portal for geeks, abgerufen am 11. Oktober 2019.
8. Eric W. Weisstein: Lebesgue Identity. Wolfram MathWorld, abgerufen am 18. Oktober 2019.
9. Titu Andreescu, Dorin Andrica, Ion Cucurezeanu: An Introduction to Diophantine Equations: A Problem-Based Approach, Theorem 2.2.3. Birkhäuser, S. 79, abgerufen am 18. Oktober 2019.