Prismatoid

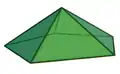
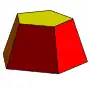
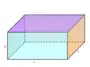
Ein Prismatoid ist ein geometrischer Körper. Es handelt sich um ein Polyeder mit parallelen Polygonen als Grund- und Deckfläche sowie Dreiecken, Trapezen oder Parallelogramme als Seitenflächen. Im Unterschied zum Prisma müssen Grund- und Deckfläche weder kongruent sein noch die gleiche Eckenzahl besitzen. Ein Prismatoid, bei dem Grund- und Deckflächen Polygone gleicher Eckenzahl sind und dessen Seitenflächen nur aus Trapezen und Parallelogrammen bestehen, wird auch als Prismoid bezeichnet.[1][2]

Das Volumen $V$ eines Prismatoids lässt sich nach der Formel[3]

V={\frac {h}{6}}(A_{G}+4A_{S}+A_{D})

berechnen. Dabei sind $A_{G}$ die Grundfläche, $A_{S}$ die Fläche bei mittlerer Höhe, $A_{D}$ die Dachfläche und $h$ die Höhe.

Dies ist eine der berühmtesten und universellsten Volumenformeln. Zu Ehren ihres Entdeckers Johannes Kepler heißt sie Keplersche Fassregel.[3]

Zu den Prismatoiden zählen:

Kein Prismatoid im eigentlichen Sinne der Definition ist das Scutoid, da es aufgrund gekrümmter Begrenzungsflächen kein Polyeder ist.

Literatur

Amos Day Bradley: Prismatoid, Prismoid, Generalized Prismoid. In: The American Mathematical Monthly. Band 86, Nr. 6, Juni/Juli 1979, S. 486–490, JSTOR 2320427.
Bruce E. Meserve, Robert E. Pingry: Some Notes on the Prismoidal Formula. In: The Mathematics Teacher. Band 45, Nr. 4, April 1952, S. 257–263, JSTOR 27954012.
Claudi Alsina, Roger B. Nelsen: A Mathematical Space Odyssey. Solid Geometry in the 21st Century (= The Dolciani Mathematical Expositions. 50). The Mathematical Association of America, Washington DC 2015, ISBN 978-0-88385-358-0, S. 85–89.

Weblinks

Eric W. Weisstein: Prismatoid. In: MathWorld (englisch).

Einzelnachweise

Claudi Alsina, Roger B. Nelsen: A Mathematical Space Odyssey. Solid Geometry in the 21st Century (= The Dolciani Mathematical Expositions. 50). The Mathematical Association of America, Washington DC 2015, ISBN 978-0-88385-358-0, S. 85-89.
Anmerkung: In der deutschen Literatur wird gelegentlich nicht zwischen Prismatoid und Prismoid unterschieden und die Begriffe stattdessen synonym verwendet, so z. B. bei Nitschke.
Martin Nitschke: Geometrie. Anwendungsbezogene Grundlagen und Beispiele für Ingenieure. 2., aktualisierte Auflage. Fachbuchverlag Leipzig im Carl-Hanser-Verlag, München 2014, ISBN 978-3-446-44143-9, S. 50-51.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Alsina-1] Claudi Alsina, Roger B. Nelsen: A Mathematical Space Odyssey. Solid Geometry in the 21st Century (= The Dolciani Mathematical Expositions. 50). The Mathematical Association of America, Washington DC 2015, ISBN 978-0-88385-358-0, S. 85-89.

[2] Anmerkung: In der deutschen Literatur wird gelegentlich nicht zwischen Prismatoid und Prismoid unterschieden und die Begriffe stattdessen synonym verwendet, so z. B. bei Nitschke.

[Nitschke-3] Martin Nitschke: Geometrie. Anwendungsbezogene Grundlagen und Beispiele für Ingenieure. 2., aktualisierte Auflage. Fachbuchverlag Leipzig im Carl-Hanser-Verlag, München 2014, ISBN 978-3-446-44143-9, S. 50-51.