p-Brane

Eine p-Brane (ausgesprochen [piːˈbɹeɪn]) ist in der Stringtheorie ein p-dimensionales Objekt. Das Wort ist von der Membran (englisch membrane) abgeleitet, eine Membran ist nach Punktteilchen (p=0) und String (p=1) das Objekt mit nächsthöherer Dimension (p=2).

Die p-Branes werden dabei in einem d-dimensionalen Raum betrachtet, für supersymmetrische Stringtheorie ist dabei d=10 mit neun Raumdimensionen und einer Zeitdimension. Werden einzelne der d=10 Dimensionen kompaktifiziert, so reduzieren sich ggf. auch einzelne der p Dimensionen eines p-Branes, so dass die effektive Theorie in d<10 Dimensionen statt der p-Branes niedrigerdimensionale Objekte enthält.

Ein Sonderfall sind die D-Branes (D nach Dirichlet, manchmal auch als Dp-Branes bezeichnet). In der M-Theorie werden p-Branes auch M-Branes genannt.

Bedeutung

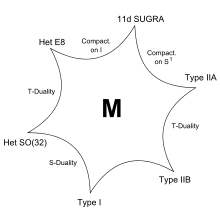
Die fünf Stringtheorien und 11-dimensionale Supergravitation als Grenzfälle der M-Theorie.

p-Branes wurden in den 1990er Jahren im Rahmen der Vereinheitlichung der fünf Stringtheorien Type I, Type IIA und IIB sowie die beiden Heterotischen Stringtheorien, im Bild mit E8 und SO(32) bezeichnet, sowie der 11-dimensionalen Supergravitation zur M-Theorie genauer betrachtet. Dabei werden die Stringtheorien und die Supergravitation als die Grenzwerte der M-Theorie mit kleiner Stringkopplungskonstante aufgefasst. Mit größer werdender Kopplungskonstante können aus eindimensionalen Strings zweidimensionale Membranen in der M-Theorie werden.[1]

Die Untersuchungen gingen dabei in unterschiedliche Richtungen: Gary Horowitz und Andrew Strominger stellten fest, dass auch höherdimensionale Objekte einen Ereignishorizont wie Schwarze Löcher haben können.[2] Joseph Polchinski betrachtete Typ-II-Superstringtheorien, die um offene Strings erweitert sind. Gibt man den offenen Strings in p+1 Dimensionen Neumann-Randbedingungen, d. h. die Ableitung verschwindet an den Endpunkten, und in den 9-p anderen Dimensionen Dirichlet-Randbedingungen, d. h. das Feld verschwindet an den Endpunkten, so bewegen sich die Endpunkte auf p-dimensionalen Objekten, den D-Branes.[3]

Wirkung

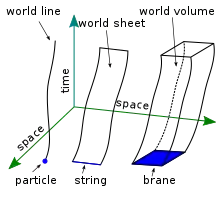
Weltlinie, Weltfläche und Weltvolumen in einer 2+1-dimensionalen Raumzeit

Im einfachsten Fall werden die Bewegungsgleichungen einer p-Brane von der Wirkung

S_{p}=-T_{p}\int d^{p+1}\xi {\sqrt {-\det(g_{ab})}}

abgeleitet, wobei $g_{ab}={\frac {\partial X^{\mu }}{\partial \xi ^{a}}}{\frac {\partial X^{\nu }}{\partial \xi ^{b}}}g_{\mu \nu }(X(\xi ))$ die induzierte Metrik ist und die Koordinaten $X^{\mu }$ die Ortskoordinaten im d-dimensionalen Raum sind. Dies ist gerade das Volumen, das das p-dimensionale Objekt mit seiner zeitlichen Entwicklung aufspannt, das sogenannte Weltvolumen. Die Euler-Lagrange-Gleichungen suchen gerade nach einem Minimum des Weltvolumens.

Sonderfall p=0

Für p=0 und konstante Metrik $g_{\mu \nu }=\eta _{\mu \nu }$ erhält man mit $T_{0}=m$

S_{0}=-m\int d\tau {\sqrt {-{\frac {dX^{\mu }}{d\tau }}{\frac {dX^{\nu }}{d\tau }}\eta _{\mu \nu }}}=-m\int d\tau {\sqrt {-{\dot {X}}^{2}}}\ .

In d=4 Dimensionen (drei Raumdimensionen und eine Zeitdimension) ist das gerade die aus der Relativitätstheorie bekannte Wirkung eines Punktteilchens. Sie ist die Länge der durch das Punktteilchen aufgespannten Weltlinie, das Punktteilchen bewegt sich auf einer Bahn, auf der die Länge dieser Weltlinie möglichst klein ist.

Das Punktteilchen ist somit gerade die p-Brane für p=0 und wird daher auch als 0-Brane oder Zero-Brane bezeichnet.

Sonderfall p=1

Für p=1 und konstante Metrik $g_{\mu \nu }=\eta _{\mu \nu }$ erhält man gerade die Nambu-Goto-Wirkung

S_{NG}=-T\int d^{2}\sigma {\sqrt {-\det \left({\frac {\partial X^{\mu }}{\partial \sigma ^{\alpha }}}{\frac {\partial X^{\nu }}{\partial \sigma ^{\beta }}}\eta _{\mu \nu }\right)}}=-T\int dA\ ,

also den Inhalt der durch einen bosonischen String aufgespannten Weltfläche. Die Dynamik des Strings minimiert diese Fläche. Der String ist die 1-Brane.

Allgemeine Wirkung

Die allgemeine p-Brane-Wirkung lautet

S_{p}=-T_{p}\int d^{p+1}\xi e^{-\Phi }{\sqrt {-\det(G_{ab}+B_{ab}+2\pi \alpha 'F_{ab})}}\ ,

wobei die p-Brane an das Dilaton $\Phi$ , die induzierte Metrik $G$ , den antisymmetrischen Tensor $B$ und einen Feldtensor $F$ gekoppelt ist.[4]

Kosmologie

Während viele der Überlegungen zu p-Branes davon ausgehen, dass die Zusatzdimensionen von uns nicht wahrgenommen werden, weil sie auf kleine Maßstäbe zusammengeschrumpft sind und nur im Rahmen der Elementarteilchenphysik erkannt werden können, so gibt es auch andere Ansätze, dass unser ganzes Universum eigentlich in einen höherdimensionalen Raum eingebettet und in diesem gerade eine Brane ist. Die ursprünglichen Betrachtungen von Gunnar Nordström und Theodor Kaluza können damit so formuliert werden, dass unsere 3+1-dimensionale Raumzeit eine 3-Brane ist, die in einem 5-dimensionalen Raum eingebettet ist.

Literatur

Brian Greene: Das elegante Universum. Siedler Verlag, 2015, ISBN 978-3-641-18565-7 (eingeschränkte Vorschau in der Google-Buchsuche).
Dieter Lüst: Quantenfische: Die Stringtheorie und die Suche nach der Weltformel. C.H.Beck, 2012, ISBN 978-3-406-62286-1 (eingeschränkte Vorschau in der Google-Buchsuche).

Einzelnachweise

Brian Greene: The Elegant Universe. W. W. Norton & Company, 2010, ISBN 978-0-393-07134-4, S. 316 (eingeschränkte Vorschau in der Google-Buchsuche).
G.T. Horowitz, A. Strominger: Black strings and p-branes. In: Nuclear Physics B. Band 360, Nr. 1, 1991, S. 197–209, doi:10.1016/0550-3213(91)90440-9.
Joseph Polchinski: Dirichlet Branes and Ramond-Ramond Charges. In: Physical Review Letters. Band 75, Nr. 26, 25. Dezember 1995, S. 4724–4727, doi:10.1103/PhysRevLett.75.4724, arxiv:hep-th/9510017.
Joseph Polchinski: String Theory, vol. I. Cambridge University Press, 1998, ISBN 1-139-45740-3, S. 270 (eingeschränkte Vorschau in der Google-Buchsuche).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Brian Greene: The Elegant Universe. W. W. Norton & Company, 2010, ISBN 978-0-393-07134-4, S. 316 (eingeschränkte Vorschau in der Google-Buchsuche).

[2] G.T. Horowitz, A. Strominger: Black strings and p-branes. In: Nuclear Physics B. Band 360, Nr. 1, 1991, S. 197–209, doi:10.1016/0550-3213(91)90440-9.

[3] Joseph Polchinski: Dirichlet Branes and Ramond-Ramond Charges. In: Physical Review Letters. Band 75, Nr. 26, 25. Dezember 1995, S. 4724–4727, doi:10.1103/PhysRevLett.75.4724, arxiv:hep-th/9510017.

[4] Joseph Polchinski: String Theory, vol. I. Cambridge University Press, 1998, ISBN 1-139-45740-3, S. 270 (eingeschränkte Vorschau in der Google-Buchsuche).