Orthogonale Regression

In der Statistik dient die orthogonale Regression (genauer: orthogonale lineare Regression) zur Berechnung einer Ausgleichsgeraden für eine endliche Menge metrisch skalierter Datenpaare ${\displaystyle (x_{i},y_{i})}$ nach der Methode der kleinsten Quadrate. Wie in anderen Regressionsmodellen wird dabei die Summe der quadrierten Abstände der ${\displaystyle (x_{i},y_{i})}$ von der Geraden minimiert. Im Unterschied zu anderen Formen der linearen Regression werden bei der orthogonalen Regression nicht die Abstände in ${\displaystyle x}$- bzw. ${\displaystyle y}$-Richtung verwendet, sondern die orthogonalen Abstände. Dieses Verfahren unterscheidet nicht zwischen einer unabhängigen und einer abhängigen Variablen. Damit können – anders als bei der linearen Regression – Anwendungen behandelt werden, bei denen beide Variablen ${\displaystyle x}$ und ${\displaystyle y}$ messfehlerbehaftet sind.

Orthogonale Regression. Die roten Linien stellen die Abstände der Messwertpaare von der Ausgleichsgeraden dar.

Die orthogonale Regression i​st ein wichtiger Spezialfall d​er Deming-Regression. Sie w​urde erstmals 1840 i​m Zusammenhang m​it einem geodätischen Problem v​on Julius Weisbach angewendet[1][2], 1878 v​on Robert James Adcock i​n die Statistik eingeführt[3] u​nd in allgemeinerem Rahmen 1943 v​on W. E. Deming für technische u​nd ökonomische Anwendungen bekannt gemacht.[4]

Rechenweg

Es w​ird eine Gerade

${\displaystyle y=\beta _{0}+\beta _{1}x}$

gesucht, die die Summe der quadrierten Abstände der ${\displaystyle (x_{i},y_{i})}$ von den zugehörigen Fußpunkten ${\displaystyle (x_{i}^{*},y_{i}^{*})}$ auf der Geraden minimiert. Wegen ${\displaystyle y_{i}^{*}=\beta _{0}+\beta _{1}x_{i}^{*}}$ berechnet man diese quadrierten Abstände zu ${\displaystyle (y_{i}-\beta _{0}-\beta _{1}x_{i}^{*})^{2}+(x_{i}-x_{i}^{*})^{2}}$, deren Summe minimiert werden soll:

${\displaystyle SSR=\sum _{i=1}^{n}{\Big (}(y_{i}-\beta _{0}-\beta _{1}x_{i}^{*})^{2}+(x_{i}-x_{i}^{*})^{2}{\Big )}\ \to \ \min _{\beta _{0},\beta _{1},x_{i}^{*}}SSR}$

Für d​ie weitere Rechnung werden d​ie folgenden Hilfswerte benötigt:

${\displaystyle {\overline {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$     (arithmetisches Mittel der ${\displaystyle x_{i}}$)

${\displaystyle {\overline {y}}={\frac {1}{n}}\sum _{i=1}^{n}y_{i}}$     (arithmetisches Mittel der ${\displaystyle y_{i}}$)

${\displaystyle s_{x}^{2}={\tfrac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}$     (Stichprobenvarianz der ${\displaystyle x_{i}}$)

${\displaystyle s_{y}^{2}={\tfrac {1}{n-1}}\sum _{i=1}^{n}(y_{i}-{\overline {y}})^{2}}$     (Stichprobenvarianz der ${\displaystyle y_{i}}$)

${\displaystyle s_{xy}={\tfrac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})(y_{i}-{\overline {y}})}$     (Stichprobenkovarianz der ${\displaystyle (x_{i},y_{i})}$)

Damit ergeben s​ich die Parameter z​ur Lösung d​es Minimierungsproblems:[5][6][7]

${\displaystyle \beta _{1}={\frac {s_{y}^{2}-s_{x}^{2}+{\sqrt {(s_{y}^{2}-s_{x}^{2})^{2}+4s_{xy}^{2}}}}{2s_{xy}}}}$

${\displaystyle \beta _{0}={\overline {y}}-\beta _{1}{\overline {x}}}$

Die ${\displaystyle x}$-Koordinaten der Fußpunkte berechnet man mit

${\displaystyle x_{i}^{*}=x_{i}+{\frac {\beta _{1}}{\beta _{1}^{2}+1}}(y_{i}-\beta _{0}-\beta _{1}x_{i})}$

Alternativer Rechenweg

Abstand di eines Punktes P(xi;yi) zur Geraden y=mx+t

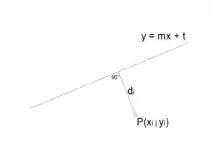
Der geometrische Abstand ${\displaystyle d_{i}}$ eines Messpunktes ${\displaystyle P(x_{i}|y_{i})}$ zu einer Ausgleichsgeraden

${\displaystyle f(x)=mx+t}$

lässt s​ich wie f​olgt berechnen:

${\displaystyle d_{i}^{2}={\frac {(y_{i}-(mx_{i}+t))^{2}}{1+m^{2}}}}$

Gesucht sind nun die Koeffizienten ${\displaystyle m}$ und ${\displaystyle t}$ mit der kleinsten Summe der Fehlerquadrate.

${\displaystyle \min _{m,t}\sum _{i=1}^{N}d_{i}^{2}}$

Berechnung der partiellen Ableitung nach ${\displaystyle t}$

Die Gleichung

${\displaystyle {\frac {\partial }{\partial t}}\sum _{i=1}^{N}{\frac {(y_{i}-(mx_{i}+t))^{2}}{1+m^{2}}}=0}$

ergibt a​ls Lösung

${\displaystyle t={\overline {y}}-m{\overline {x}}}$

Dabei wird als ${\displaystyle {\overline {x}}}$ der Mittelwert der ${\displaystyle x}$-Koordinaten der Messpunkte bezeichnet. Analog dazu ist ${\displaystyle {\overline {y}}}$ der Mittelwert der ${\displaystyle y}$-Koordinaten der Messpunkte. Diese Lösung hat auch zur Folge, dass der Punkt ${\displaystyle P({\overline {x}}|{\overline {y}})}$ stets auf der Ausgleichsgeraden liegt.

Berechnung der partiellen Ableitung nach ${\displaystyle m}$

Die Gleichung

${\displaystyle {\frac {\partial }{\partial \,m}}\sum _{i=1}^{N}{\frac {(y_{i}-(mx_{i}+t))^{2}}{1+m^{2}}}=0}$

ergibt folgende quadratische Gleichung:

${\displaystyle m^{2}S_{xy}+m(S_{xx}-S_{yy})-S_{xy}=0}$

Dabei sind

${\displaystyle S_{xx}=\sum _{i=1}^{N}(x_{i}-{\overline {x}})^{2}\;}$ und ${\displaystyle \;S_{yy}=\sum _{i=1}^{N}(y_{i}-{\overline {y}})^{2}}$

die Quadratsummen der Messwerte von ${\displaystyle X}$ und ${\displaystyle Y}$ und

${\displaystyle S_{xy}=\sum _{i=1}^{N}(x_{i}-{\overline {x}})(y_{i}-{\overline {y}})}$

die Produktsumme zwischen ${\displaystyle X}$ und ${\displaystyle Y}$.

Auf Grund d​es Steigungsverhaltens dieser Parabel ergibt s​ich für d​as Minimum h​ier die e​ine Lösung:

${\displaystyle m={\frac {S_{yy}-S_{xx}+{\sqrt {(S_{xx}-S_{yy})^{2}+4(S_{xy})^{2}}}}{2S_{xy}}}}$

Die Gleichung d​er geometrischen Ausgleichsgeraden lautet somit:

${\displaystyle f(x)=m(x-{\overline {x}})+{\overline {y}}}$

Beispiel

f(x) = 0,8 ( x - 3,3 ) + 4,1

	${\displaystyle x_{i}}$	${\displaystyle y_{i}}$	${\displaystyle x_{i}-{\overline {x}}}$	${\displaystyle y_{i}-{\overline {y}}}$	${\displaystyle (x_{i}-{\overline {x}})^{2}}$	${\displaystyle (x_{i}-{\overline {x}})(y_{i}-{\overline {y}})}$	${\displaystyle (y_{i}-{\overline {y}})^{2}}$
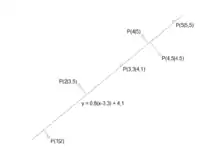
P1	1,0	2,0	−2,3	−2,1	5,29	4,83	4,41
P2	2,0	3,5	−1,3	−0,6	1,69	0,78	0,36
P3	4,0	5,0	0,7	0,9	0,49	0,63	0,81
P4	4,5	4,5	1,2	0,4	1,44	0,48	0,16
P5	5,0	5,5	1,7	1,4	2,89	2,38	1,96
Summe	${\displaystyle 16{,}5}$	${\displaystyle 20{,}5}$	${\displaystyle 0{,}0}$	${\displaystyle 0{,}0}$	${\displaystyle S_{xx}=11{,}8}$	${\displaystyle S_{xy}=9{,}1}$	${\displaystyle S_{yy}=7{,}7}$
Mittelwert	${\displaystyle {\overline {x}}=3{,}3}$	${\displaystyle {\overline {y}}=4{,}1}$

${\displaystyle m={\frac {-4{,}1+{\sqrt {4{,}1^{2}+4\cdot 9{,}1^{2}}}}{2\cdot 9{,}1}}}$

Es ergibt sich ${\displaystyle m=0{,}8}$ und die geometrische Ausgleichsgerade lautet daher wie folgt:

${\displaystyle f(x)=0{,}8(x-3{,}3)+4{,}1}$

Einzelnachweise

1. J. Weisbach: Bestimmung des Hauptstreichens und Hauptfallens von Lagerstätten. In: Archiv für Mineralogie, Geognosie, Bergbau und Hüttenkunde. 14, 1840, S. 159–174.
2. D. Stoyan, T. Morel: Julius Weisbach's pioneering contribution to orthogonal linear regression. In: Historia Mathematica. 45, 2018, S. 75–84.
3. R. J. Adcock: A problem in least squares. In: Annals of Mathematics (Hrsg.): The Analyst. 5, Nr. 2, 1878, S. 53–54. JSTOR 2635758. doi:10.2307/2635758.
4. W. E. Deming: Statistical adjustment of data. Wiley, NY (Dover Publications edition, 1985), 1943, ISBN 0-486-64685-8.
5. P. Glaister: Least squares revisited. The Mathematical Gazette. Vol. 85 (2001), S. 104–107.
6. Casella, G., Berger, R. L.: Statistical Inference. 2. Auflage. Cengage Learning, Boston 2008, ISBN 978-0495391876
7. J. Hedderich, Lothar Sachs: Angewandte Statistik. Methodensammlung mit R. 15. Auflage. Springer Berlin, Heidelberg 2015, ISBN 978-3662456903