Optische Mitte

Optische Mitte ist ein Begriff der Gestaltungslehre und Wahrnehmungspsychologie. Er bezeichnet einen Punkt, der leicht von der geometrischen Mitte eines Objektes abweicht und aufgrund einer optischen Täuschung optisch als Mitte wahrgenommen wird, was beispielsweise in Grafik und Design berücksichtigt werden muss.

Optische Mitte in Grafik und Design

Links: geometrische Mitte.
Rechts: optische Mitte.
Format: DIN A4

Eine absolute Berechnungsgrundlage für die optische Mitte gibt es nicht. Sie wird bei der Herstellung oft nach Gefühl gewählt.

Die optische Mitte kommt überall dort zum Einsatz, wo typografische, bildliche oder inhaltliche Elemente in einem umgebenden Format vertikal mittig platziert werden sollen. Die optische Mitte fällt stärker ins Gewicht, wenn die Elemente auch horizontal zentriert werden.

Balancelinie

Links: Konstruktion der Balancelinie nach Hallberg.
Rechts: Anwendung.
Format: DIN A4

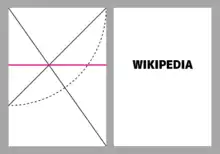
Nach Hallberg[1] lässt sich eine Balancelinie konstruieren, um die sich die einzelnen Elemente harmonisch und ausgewogen gruppieren, um einen optischen Ausgleich zu schaffen.

Sei b die Seitenbreite (210 mm für A4 hochkant) und h ihre Höhe (297 mm) sowie x der horizontale und y der vertikale Abstand von der oberen linken Ecke zum Schnittpunkt der Rechteckdiagonalen (von oben links nach unten rechts) mit der Quadratdiagonalen (von oben rechts nach links, entspricht der Viertelkreissekante).

Die Höhe y der Balancelinie kann mithilfe des Strahlensatzes berechnet werden. Der Strahlensatz muss dafür sowohl für die Rechteckdiagonale als auch für die Quadratdiagonale angewendet werden. Der Strahlensatz für die Rechteckdiagonale lautet:

{\frac {y}{h}}={\frac {x}{b}}\qquad \Longleftrightarrow \qquad x={\frac {b}{h}}\times y

Da die Kantenlängen eines Quadrates gleich sind, kann der Strahlensatz für die Quadratdiagonale folgendermaßen geschrieben werden:

{\frac {y}{b}}={\frac {b-x}{b}}\qquad \Longleftrightarrow \qquad y=b-x

Setzt man die zweite in die erste Gleichung ein, kann y berechnet werden:

y=b-{\frac {b}{h}}\times y\qquad \Longleftrightarrow \qquad y={\frac {b}{1+{\frac {b}{h}}}}={\frac {b\times h}{b+h}}

Für eine A4-Seite ergibt sich also $y={\tfrac {210\times 297}{210+297}}\,{\text{mm}}\approx 123\,{\text{mm}}$ von oben bzw. 174 mm von unten, was aufgrund des speziellen Seitenverhältnisses (1 ∶ √2) genau $2\times (297-210)\,{\text{mm}}$ von unten entspricht.

Belege

Symmetrie, Asymmetrie. Uta.fi. Abgerufen am 13. Juli 2010.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Symmetrie, Asymmetrie. Uta.fi. Abgerufen am 13. Juli 2010.