Operatorenrechnung nach Heaviside

Die Operatorenrechnung nach Heaviside beschreibt eine nach Oliver Heaviside benannte empirische Operatorenrechnung, welche 1887 in seinem berühmten Werk „Electromagnetic Theory“ veröffentlicht wurde. (englisch operator calculus oder operational calculus)

Allgemeines

Der Sinn der Operatorenrechnung ist es bei der Lösung von Differentialgleichungen die Operation des Differenzierens durch die algebraische Operation des Multiplizierens mit einem Operator zu ersetzen und damit eine meist relativ schwierig lösbare Differentialgleichung in eine leichter lösbare algebraische Gleichung zu „transformieren“. Heaviside baute, basierend auf Vorarbeiten von Leibniz und Cauchy, als erster die Operatorenrechnung zu einem Kalkül aus und löste damit viele der zur damaligen Zeit anstehenden theoretischen Probleme der Elektrotechnik.

Dazu verallgemeinerte er die komplexe Wechselstromrechnung, in der $\mathrm {j} \omega ={\frac {d}{dt}}$ die Differentiation ersetzt, indem er den Differentialoperator $p={\frac {d}{dt}}$ einführt und ihn ohne tiefere Begründung wie einen multiplikativen Faktor nutzt:

p\cdot f(t)={\frac {d}{dt}}f(t)={\frac {df(t)}{dt}}=f'(t)

Schließlich trennt er $p$ von den Zeitfunktionen und gibt den entstehenden Ausdrücken eine „eigene Existenz“ als Operator. Intuitiv folgert er, dass der Kehrwert ${\frac {1}{p}}$ logischerweise den Operator für die Integration darstellt.

Die Heavisidesche Operatorenrechnung (auch als Heaviside-Kalkül bezeichnet) stellt eine Verallgemeinerung der erweiterten symbolischen Methode auf nichtstationäre Signale dar und ist damit ein Vorläufer der modernen Operatorenrechnungen, wie der Laplacetransformation und der Operatorenrechnung nach Mikusiński.

Beispiel

RC-Glied

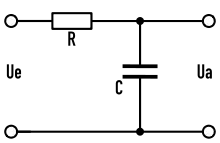
Es soll der Verlauf der Spannung von u_a(t) am Kondensator eines RC-Gliedes berechnet werden, wenn an dessen Eingang die Gleichspannung U_e zum Zeitpunkt t = 0 „eingeschaltet“ wird. Mit der Schreibweise von Heaviside für den Einheitssprung als „fette Eins“ gilt also u_e(t) = U_e·1.

Aus der Schaltung erhält man die Beziehung

i_{C}=C\cdot {\frac {du_{a}}{dt}}={\frac {u_{e}-u_{a}}{R}}

Daraus folgt die inhomogene DGL für t ≥ 0:

RC\cdot {\frac {du_{a}}{dt}}+u_{a}=U_{e}

.

Heaviside setzt nun den Differentialoperator p ein:

RC\cdot p\cdot u_{a}+u_{a}=U_{e}

Er klammert aus

(RC\cdot p+1)\cdot u_{a}=U_{e}

… und löst nach der gesuchten Größe auf

u_{a}={\frac {U_{e}}{1+pCR}}

.

Damit ist zwar der „Operator für das Ergebnis“ gefunden, aber was bedeutet dieser Ausdruck? Heaviside versucht die Lösung durch Reihenentwicklung:

u_{a}={\frac {U_{e}}{pCR}}\cdot {\frac {1}{1+{\frac {1}{pCR}}}}={\frac {U_{e}}{pCR}}\cdot \left(1-{\frac {1}{pCR}}+{\frac {1}{(pCR)^{2}}}-{\frac {1}{(pCR)^{3}}}+...\right)=U_{e}\cdot \left({\frac {1}{pCR}}-{\frac {1}{(pCR)^{2}}}+{\frac {1}{(pCR)^{3}}}-{\frac {1}{(pCR)^{4}}}+...\right)

Indem man ${\frac {1}{p}}$ als Integrationsoperator (angewendet auf den Einheitssprung) interpretiert, erhält man die Reihenglieder (die aber für t < 0 verschwinden):

{\frac {1}{pCR}}\cdot 1={\frac {1}{RC}}\int _{0}^{t}1\cdot d\tau =t/RC

{\frac {1}{(pCR)^{2}}}\cdot 1={\frac {1}{pCR}}\cdot \left({\frac {1}{pCR}}\cdot 1\right)={\frac {1}{(RC)^{2}}}\int _{0}^{t}\tau \cdot d\tau ={\frac {(t/RC)^{2}}{2}}

und allgemein

{\frac {1}{(pCR)^{n}}}\cdot 1={\frac {(t/RC)^{n}}{n!}}

.

Also

u_{a}=U_{e}\cdot \left(t/RC-{\frac {(t/RC)^{2}}{2}}+{\frac {(t/RC)^{3}}{6}}-{\frac {(t/RC)^{4}}{24}}+...\right)=U_{e}\cdot \left(1-\left(1-t/RC+{\frac {(t/RC)^{2}}{2}}-{\frac {(t/RC)^{3}}{6}}+{\frac {(t/RC)^{4}}{24}}-...\right)\right)

Hier muss man nun – wie Heaviside – „mit geschultem Auge“ erkennen, dass sich hinter dieser Reihe die Exponentialfunktion (mit negativem Argument) versteckt und erhält damit die in sich geschlossene Lösung (für t ≥ 0):

u_{a}=U_{e}\cdot \left(1-e^{-t/RC}\right)

.

Die Übertragungsfunktion

Heaviside definiert nun als Charakteristik des Systems eine von den Signalen unabhängige Übertragungsfunktion als Operator. Für das o. g. Beispiel erhält man:

H={\frac {u_{a}}{u_{e}}}={\frac {1}{1+pCR}}

.

Diese Definition ist identisch mit der Übertragungsfunktion im Sinne der erweiterten symbolischen Methode der Wechselstromtechnik und anderer Operatorenrechnungen und hat noch heute überragende Bedeutung.

Deutung durch Zerlegung

Heaviside deutete die in Operatorform erhaltenen Ergebnisse durch Partialbruchzerlegung oder Reihenentwicklung (wie im obigen Beispiel). Für die Partialbruchzerlegung entwickelte Heaviside eine zuverlässige Methode, die selbst in den modernen Operatorenrechnungen noch als Heavisidescher Entwicklungssatz benutzt wird. Praktisch gibt es dabei allerdings Probleme mit der Bestimmung der Wurzeln, wenn der Grad des zu zerlegenden Nenner-Polynoms größer als 4 ist, wenn eine Wurzel 0 ist oder mehrfach auftritt.

Im Gegensatz dazu ist die Zerlegung durch Reihenentwicklung prinzipiell recht schwierig und, je nach Ansatz, verschieden möglich. Das Ergebnis wird mehrdeutig und damit ist diese Methode „für die praktische Ingenieurtätigkeit nicht gut geeignet“. Zerlegt man im o. g. Beispiel den Operator wie folgt in eine Potenzreihe

u_{a}=U_{e}\cdot {\frac {1}{1+pCR}}=U_{e}\cdot \left(1-pCR+(pCR)^{2}-(pCR)^{3}+...\right)

und interpretiert p als Differentialoperator, dann erhält man ein falsches bzw. sinnloses Ergebnis. Um sicherzugehen, wären mathematisch umfangreiche Untersuchungen zur Konvergenz bzw. Divergenz der Potenzreihen erforderlich.

Kritik

Heaviside betrachtet die Mathematik als Experimentalwissenschaft und meinte, dass der Erfolg das Verfahren rechtfertigt. Er machte keinen Unterschied zwischen den Operatoren und den Objekten, auf welche er sie anwendete. Dazu wäre eine mathematische Körpertheorie nötig gewesen, die aber zur damaligen Zeit noch nicht ausgearbeitet war. Heaviside setzte immer (implizit) verschwindende Anfangsbedingungen der Differentialgleichungen voraus, also „entladene Energiespeicher“ zum Zeitpunkt 0. Obwohl Heaviside viele damals aktuelle Probleme mit seiner Operatorenrechnung löste, konnte sie sich nicht durchsetzen und war vielen „Angriffen“ der Mathematiker ausgesetzt. Erst durch die Interpretation der Operatoren mit Hilfe der Laplacetransformation konnte sich die Operatorenrechnung auf der Basis der Integraltransformation und der Funktionentheorie in Theorie und Praxis etablieren. Schließlich wurde 1950 vom Mathematiker Jan Mikusiński eine Operatorenrechnung „ohne Laplacetransformation“ mit algebraischen Methoden mathematisch exakt begründet.

Weblinks

Heaviside’s Operator Calculus (englisch)

Literatur

Oliver Heaviside: Electromagnetic Theory, Volume 1 (Classic Reprint). Forgotten Books, 2010, ISBN 978-1-4400-8252-8 (Online).
Oliver Heaviside: Electromagnetic Theory, Volume 2 (Classic Reprint). Forgotten Books, 2010, ISBN 978-1-4400-8877-3 (Online).
Oliver Heaviside: Electromagnetic Theory, Volume 3 (Classic Reprint). Forgotten Books, 2010, ISBN 978-1-4400-8253-5 (Online).
F. H. Lange: Signale und Systeme - Band 1: Spektrale Darstellung. Verlag Technik, Berlin 1965.
Gerhard Wunsch: Geschichte der Systemtheorie. Akademie-Verlag., Leipzig 1985.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.