Moser-Spindel
Die Moser-Spindel ist ein Graph, der nach den Gebrüdern William Oscar Jules und Leo Moser benannt wurde.[1] Es handelt sich dabei um einen ungerichteten Graphen mit sieben Knoten und elf Kanten. Die Moser-Spindel lässt sich als Einheitsdistanz-Graph und als ebener Graph in die Ebene einbetten, ist jedoch kein Streichholzgraph. Eine ihrer Anwendungen ist der Beweis, dass die chromatische Zahl der Ebene größer oder gleich vier ist.[2] Damit erhält man eine untere Schranke für das Hadwiger-Nelson-Problem.
Die Moser-Spindel ist auch unter dem Namen Hajós-Graph (nach György Hajós) bekannt.[3]
Konstruktion
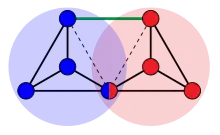
Die Moser-Spindel lässt sich mit geometrischen Mitteln, oder, alternativ dazu, auch mit rein graphentheoretischen Überlegungen konstruieren.
Ausgangspunkt für die geometrische Konstruktion ist ein gleichseitiges Dreieck der Kantenlänge eins, welches an einer seiner Seiten gespiegelt wird. Die entstandene Figur ist eine Raute mit den Innenwinkeln 60° und 120°. Zwei solcher Rauten werden nun so in der Ebene positioniert, dass sie sich einen spitzwinkligen Eckpunkt teilen und die beiden jeweils gegenüberliegenden Ecken voneinander den Einheitsabstand haben. Die elf Kanten des Graphen entsprechen den Seiten der gleichseitigen Dreiecken und der Strecke zwischen den beiden spitzwinkligen Ecken der Rauten.
Rein graphentheoretisch lässt sich die Moser-Spindel mittels der Hajós-Konstruktion, ausgehend von zwei vollständigen Graphen K4 konstruieren. Bei dieser Konstruktion wird von beiden Graphen jeweils eine Kante entfernt. Von den jeweiligen Endpunkten dieser entfernten Kante wird ein Paar zusammengelegt und das andere Paar mit einer neuen Kante verbunden.[4]
Anwendung auf das Hadwiger–Nelson-Problem
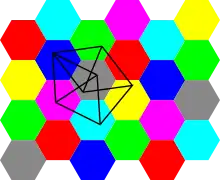
Das Hadwiger-Nelson-Problem untersucht die minimal benötigte Anzahl an Farben, um eine Ebene derart einzufärben, dass jeweils zwei Punkte mit Einheitsabstand unterschiedliche Farben besitzen. Gesucht ist also die chromatische Zahl jenes Einheitsdistanz-Graphen, dessen Knoten alle Punkte der Ebene sind.[2] Die Moser-Spindel ist ein Teilgraph jenes Graphen. Daraus folgt, dass man für die Färbung der Ebene mindestens so viele Farben benötigt wie zur Färbung der Moser-Spindel.
Es kann gezeigt werden, dass die chromatische Zahl der Moser-Spindel vier beträgt: Da die Moser-Spindel Dreiecke beinhaltet, sind mindestens drei Farben notwendig. Nimmt man an, dass bereits drei Farben ausreichen, dann haben der Knoten, den sich beide Rauten teilen, sowie die beiden jeweils gegenüberliegenden Eckpunkte der Rauten dieselbe Farbe. Dies führt zu einem Widerspruch. Vier Farben reichen jedoch aus, um die Moser-Spindel einzufärben.[4]
Vier ist damit eine untere Schranke für die chromatische Zahl der Ebene.
Der Satz von de Bruijn–Erdős besagt, dass unter der Voraussetzung des Auswahlaxioms die chromatische Zahl eines unendlichen Graphen gleich der größten chromatischen Zahl eines endlichen Teilgraphen ist. Bis 2018 war kein endlicher Teilgraph bekannt, der mehr Farben als die Moser-Spindel benötigt. Die beste bekannte obere Schranke für das Hadwiger–Nelson-Problem beträgt sieben.[2]
Weitere Eigenschaften
Die Moser-Spindel ist ein Laman-Graph, das heißt, sie ist ein minimaler starrer Graph in der Ebene.[5]
Der zu der Moser-Spindel komplementäre Graph ist ein dreiecksfreier Graph. Daraus folgt, dass unter drei Knoten der Moser-Spindel (betrachtet als Einheitsdistanz-Graph) immer mindestens ein Knotenpaar ist, das voneinander Einheitsabstand hat.[2][6]
Beim Hinzufügen von weiteren Kanten geht stets die Einheitsdistanz-Eigenschaft verloren. Außerdem gibt es keinen Graphenhomomorphismus, der die Moser-Spindel auf einen kleineren Einheitsdistanz-Graph abbildet. Diese beiden Eigenschaften wurden von Horvat, Kratochvíl und Pisanski verwendet, um zu beweisen, dass das Testen, ob ein gegebener Graph eine Einbettung als Einheitsdistanz-Graph hat, ein NP-schweres Problem ist.[5]
Eine n-dimensionale Verallgemeinerung der Moser-Spindel spielt eine wichtige Rolle bei dem Beweis des Satzes von Beckman und Quarles.[7]
Einzelnachweise
- W. und L. Moser: Solution to problem 10. In: Can. Math. Bull. Band 4, 1961, S. 187–189.
- A. Soifer: The Mathematical Coloring Book: Mathematics of Coloring and the Colorful Life of its Creators. Springer, New York 2008, ISBN 978-0-387-74640-1, S. 14–15.
- J. A. Bondy, U. S. R. Murty: Graph Theory. In: Graduate Texts in Mathematics. Band 244. Springer, 2008, S. 358, doi:10.1007/978-1-84628-970-5.
- G. Hajós: Über eine Konstruktion nicht n-färbbarer Graphen. In: Wiss. Z. Martin-Luther-Univ. Halle-Wittenberg Math.-Natur. Reihe. Band 10, 1961, S. 116–117.
- Boris Horvat, Jan Kratochvíl, Tomaž Pisanski: On the Computational Complexity of Degenerate Unit Distance Representations of Graphs. In: Lecture Notes in Computer Science. Band 6460, 2011, S. 274–285.
- Peter Winkler: Puzzled: Distances Between Points on the Plane. In: Communications of the ACM. Band 54, Nr. 11, doi:10.1145/2018396.2018422.
- W. Benz: Geometrische Transformationen unter besonderer Berücksichtigung der Lorentztransformation. BI-Wiss.-Verl., Mannheim (u. a.) 1992, ISBN 3-411-15071-8, S. 15–31.