Message Authentication Code
Ein Message Authentication Code (MAC; deutsch Nachrichtenauthentifizierungscode[1]) dient dazu, Gewissheit über den Ursprung von Daten oder Nachrichten zu erhalten und ihre Integrität zu überprüfen.[2] MAC-Algorithmen erfordern zwei Eingabeparameter, erstens die zu schützenden Daten und zweitens einen geheimen Schlüssel, und berechnen aus beidem eine Prüfsumme, den Message Authentication Code.[2]
Funktionsweise
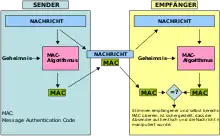
Die Integrität einer zu übertragenden Nachricht lässt sich mittels MACs wie folgt prüfen:[3] Zunächst vereinbaren Sender und Empfänger einen geheimen Schlüssel. Der Sender berechnet für diesen Schlüssel und seine Nachricht einen MAC und sendet dann die Nachricht sowie den MAC an den Empfänger. Dieser berechnet den MAC zu der empfangenen Nachricht mit dem Schlüssel und vergleicht den berechneten MAC mit dem empfangenen. Die Übereinstimmung beider Werte interpretiert der Empfänger als erfolgreichen Integritätstest: Die Nachricht wurde von einer Partei abgeschickt, die den geheimen Schlüssel kennt, und sie wurde während der Übertragung nicht verändert.
MACs schützen nicht vor Replay-Angriffen. Dazu muss die Nachricht selbst Daten enthalten, die sicherstellen, dass Wiederholungen entdeckt werden können (z. B. Zeitstempel, Sequenznummer oder durch die Verwendung von Einmal-MACs).
Bestimmung des MACs
MACs basieren entweder auf Blockchiffren oder auf Hash-Funktionen oder sind speziell entwickelte MACs. Ein gebräuchliches Verfahren zur MAC-Berechnung, der HMAC, basiert auf kryptographischen Hash-Funktionen und wird beispielsweise in SSL und IPsec eingesetzt.[4] Ein verbreitetes Verfahren basierend auf Blockchiffren ist der in der NIST Special Publication 800-38B spezifizierte Cipher-Based Message Authentication Code (CMAC), der in Verbindung mit AES oder Triple DES verwendet wird.[5] Ein älteres Verfahren zur Berechnung eines MAC auf Basis des DES und CBC ist als ANSI X9.9 standardisiert, wurde aber inzwischen aufgrund von Sicherheitsmängeln widerrufen.[6] Ein spezieller MAC ist der Message Authentication Algorithm (MAA), der 1983 als ein Standard für Banken entwickelt wurde.
Abgrenzung von Hashfunktionen und digitalen Signaturen
Kryptographische Hashfunktionen können zur Berechnung von MACs genutzt werden, jedoch gehen MACs über die Verwendung einfacher Hashwerte hinaus:[7] Wenn eine Nachricht nur mit ihrem Hashwert als MAC übertragen würde, wäre dies nicht sicher, da die Hashfunktion öffentlich bekannt ist. Ein Angreifer könnte die Nachricht modifizieren und einen neuen Hashwert für die neue Nachricht berechnen und diesen übertragen. Falls allerdings Sender und Empfänger ein Geheimnis teilen, kann dies in die Hashberechnung einfließen, so dass ein Angreifer nach Modifikation einer Nachricht nicht in der Lage ist, den passenden Hashwert zu berechnen.
Auch wenn die Manipulationssicherheit von MACs eine Verwandtschaft mit digitalen Signaturen nahelegt, bestehen Unterschiede der beiden Verfahren. MACs unterscheiden sich von digitalen Signaturen darin, dass die Überprüfung des MACs Kenntnis desselben geheimen Schlüssels erfordert, der zu seiner Berechnung genutzt wurde.[8] Daher kann jeder, der einen MAC überprüfen kann, diesen auch berechnen;[8] entsprechend ist er nicht in der Lage, gegenüber Dritten zu beweisen, von wem die Nachricht stammt. Im Gegensatz dazu werden digitale Signaturen mit Hilfe eines nur dem Absender bekannten Schlüssels erstellt und mit Hilfe eines öffentlichen Schlüssels überprüft.[8] So ist sichergestellt, dass der Unterschreiber im Besitz des privaten Schlüssels ist, und es sich so mit hoher Wahrscheinlichkeit um den vorgegebenen Autor der Nachricht handelt.
Informationstheoretisch sichere Verfahren
Beispiel
Ein Klartextbit (A oder B) soll mittels einer 1-Bit MAC authentisiert übertragen werden. Der Schlüssel ist zwei Bit lang.
| Schlüssel | (A,0)* | (A,1)* | (B,0)* | (B,1)* |
|---|---|---|---|---|
| 00 | A | B | ||
| 01 | A | B | ||
| 10 | A | B | ||
| 11 | A | B |
* (Text,MAC)
Die Nachricht AABB unter dem (zuvor vereinbarten) geheimen Schlüssel 11000110 wird dann als (A,1)(A,0)(B,1)(B,0) übertragen.
Sicherheitsanalyse
Angenommen ein Angreifer fängt das erste übertragene Paar aus obigem Beispiel ab und versucht, anstelle des A ein B zu übersenden. Damit die Änderung nicht bemerkt wird und er nicht auffällt, benötigt er den passenden MAC. Ihm ist aus der Übersicht bekannt, dass der entsprechende Schlüsselabschnitt 10 oder 11 lautet. Mit diesem Wissen ist es ihm aber nicht möglich, sich zwischen (B,0) und (B,1) zu entscheiden. Genau vor der gleichen Entscheidung steht er auch ohne Kenntnis des Schlüsselabschnitts, also der Frage MAC=0 oder MAC=1. Er rät also durchschnittlich in jedem zweiten Fall richtig.
Über diesen Sachverhalt kann man allgemein informationstheoretische Sicherheit definieren.
- (zur Notation siehe Bedingte Wahrscheinlichkeit)
In Worten: Unabhängig von der a priori Kenntnis über den Klartext x erhält ein Angreifer durch Sehen des Schlüsseltextes S (hier: Klartext und MAC) oder von Teilen davon keine Information hinzu. Damit ist absolute Sicherheit nach Shannon gegeben.
Bei allen Betrachtungen wird natürlich vorausgesetzt, dass das beschriebene System korrekt funktioniert und auch so benutzt wird. Fällt dem Angreifer z. B. der geheime Schlüssel (oder -teile) in die Hand, so sind auch informationstheoretisch sichere Systeme zu brechen.
Eigenschaften
Die folgenden Eigenschaften beziehen sich auf den allgemeinen Fall. Im Speziellen gibt es abgeleitete effizientere Verfahren gleicher Qualität.
Die Fehlerwahrscheinlichkeit (am Beispiel: 0,5) bestimmt sich aus der Länge des pro Nachrichtenbit verwendeten MAC (am Beispiel: 1)
Da es immer einen passenden und damit zufällig zu erratenen MAC geben muss, kann auch durch die Verlängerung des MAC keine Wahrscheinlichkeit gleich Null garantiert werden. Durch den asymptotischen Zusammenhang nähert sich die Wahrscheinlichkeit aber schnell vernachlässigbaren Dimensionen.
Die nötige Schlüssellänge (am Beispiel: 2) bestimmt sich durch . Möchte man also eine Nachricht der Länge übertragen, sind Schlüsselbits (am Beispiel: 8) nötig.
Analog zum One-Time-Pad stellt sich hier ebenfalls die Frage, wie viele Schlüssel notwendig sind, um die gewünschte und eben beschriebene Sicherheit zu gewährleisten. Allgemein wird dieser Wert mit angegeben. Damit ist das obige Beispiel mit der angegebenen Dimensionierung (u. a. Größe von MAC und Schlüssel) optimal.
Literatur
- Charlie Kaufman, Radia Perlman, Mike Speciner: Network Security: Private Communication in a Public World. Prentice Hall PTR, Upper Saddle River, New Jersey 2002, ISBN 0-13-046019-2.
- Alfred J. Menezes, Paul C. van Oorschot, Scott A. Vanstone: Handbook of Applied Cryptography. CRC Press, 2001, ISBN 0-8493-8523-7. (online)
- William Stallings: Cryptography and Network Security: Principles and Practice. 5. Auflage. (International Edition), Prentice Hall, 2011, ISBN 978-0-13-705632-3.
Einzelnachweise
- dict.cc: message authentication code <MAC> | Nachrichtenauthentifizierungscode
- Menezes u. a.: Handbook of Applied Cryptography. S. 323.
- Menezes u. a.: Handbook of Applied Cryptography. S. 364.
- Stallings: Cryptography and Network Security: Principles and Practice. S. 400.
- Stallings: Cryptography and Network Security: Principles and Practice. S. 404.
- X9 Committee: Withdrawal of ANSI X9.9, Financial Institution Message Authentication (PDF; 157 kB) Archiviert vom Original am 5. Februar 2007. Abgerufen am 9. November 2011.
- Kaufman u. a.: Network Security: Private Communication in a Public World. S. 56.
- Kaufman u. a.: Network Security: Private Communication in a Public World. S. 51.