Merkles Meta-Verfahren

Merkles Meta-Verfahren (auch Merkle-Damgård-Konstruktion) i​st eine Methode z​ur Konstruktion v​on kryptographischen Hash-Funktionen, d​ie auf Arbeiten v​on Ralph Merkle u​nd Ivan Damgård zurückgeht.

Gegeben ist eine Kompressionsfunktion ${\displaystyle f\colon \{0,1\}^{a+b}\rightarrow \{0,1\}^{b}}$, die eine ${\displaystyle a+b}$ Bit lange Eingabe auf eine ${\displaystyle b}$ Bit lange Ausgabe abbildet. Sie ist kollisionssicher, das heißt, es ist nicht mit realistischem Aufwand möglich, zwei verschiedene Eingaben zu finden, die auf die gleiche Ausgabe abgebildet werden. Durch die Anwendung von Merkles Meta-Verfahren ergibt sich daraus eine kollisionssichere Hash-Funktion ${\displaystyle h\colon \{0,1\}^{*}\rightarrow \{0,1\}^{b}}$, die beliebig lange Nachrichten auf einen Hashwert von ${\displaystyle b}$ Bit abbildet.

Vorgehensweise

Aus den Nachrichtenblöcken wird durch wiederholte Anwendung der Kompressionsfunktion der Hashwert erzeugt

Die Nachricht ${\displaystyle m}$ wird zunächst mit einem Padding-Verfahren zu ${\displaystyle {\overline {m}}}$ erweitert, so dass die Länge von ${\displaystyle {\overline {m}}}$ ein Vielfaches der Blockgröße ${\displaystyle a}$ ist. Dann wird ${\displaystyle {\overline {m}}}$ in ${\displaystyle n}$ Blöcke der Länge ${\displaystyle a}$ aufgeteilt:

${\displaystyle {\overline {m}}=m_{1}\|m_{2}\|\ldots \|m_{n}}$ mit ${\displaystyle |m_{i}|=a}$.

Die Kompressionsfunktion ${\displaystyle f}$ wird iterativ auf die ${\displaystyle b}$ Bit lange Ausgabe der vorherigen Iteration und den nächsten Block ${\displaystyle m_{i}}$ der erweiterten Nachricht angewandt, bis diese ganz verarbeitet ist. Bei der ersten Iteration besteht die Eingabe aus einem ${\displaystyle b}$ Bit langen Initialisierungsvektor ${\displaystyle H_{0}}$, häufig mit dem Wert 0, und dem ersten Nachrichtenblock ${\displaystyle m_{1}}$.

${\displaystyle H_{i}:=f(H_{i-1}\|m_{i});\quad 1\leq i\leq n}$.

Der Hash-Wert wird dann aus der letzten Kompressionsausgabe durch eine Finalisierungsfunktion berechnet: ${\displaystyle h=\operatorname {final} (H_{n})}$. Die Finalisierungsfunktion ist häufig die Identität oder eine Trunkierung.

Davies-Meyer-Kompressionsfunktion

Matyas–Meyer–Oseas-Kompressionsfunktion

Miyaguchi-Preneel-Kompressionsfunktion

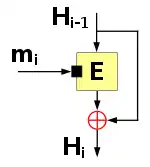
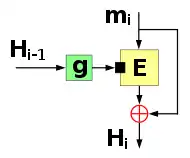
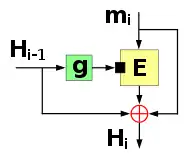
Als Kompressionsfunktion wird häufig eine Blockverschlüsselung eingesetzt, wofür es hauptsächlich zwei Möglichkeiten gibt: Die Davies-Meyer-Kompressionsfunktion nutzt den Nachrichtenblock ${\displaystyle m_{i}}$ als Schlüssel, um damit den Verkettungswert ${\displaystyle H_{i-1}}$ zu verschlüsseln. Danach wird noch der so berechnete Schlüsseltext mit dem Klartext verknüpft (oft durch bitweises XOR). Dadurch wird die Eigenschaft einer Blockchiffre aufgehoben, den Klartext bijektiv auf den Schlüsseltext abzubilden, und die Abbildung von ${\displaystyle H_{i-1}}$ auf ${\displaystyle H_{i}}$ ähnelt wesentlich mehr einer Zufallsfunktion. Sonst wäre die Kompressionsfunktion auch nicht kollisionssicher, denn ein Angreifer könnte ${\displaystyle H_{i}}$ vorgeben und mit verschiedenen ${\displaystyle m_{i}}$ entschlüsseln.

Die Matyas–Meyer–Oseas-Kompressionsfunktion verschlüsselt den Nachrichtenblock mit dem Verkettungswert als Schlüssel. Auch hier werden Klar- und Schlüsseltext anschließend verknüpft. Zur Anpassung an die gegebene Schlüssellänge muss evtl. ${\displaystyle H_{i-1}}$ mit einer Funktion ${\displaystyle g}$ erweitert oder komprimiert werden. Als Modifikation von Matyas–Meyer–Oseas gibt es noch die Miyaguchi-Preneel-Kompressionsfunktion, die sich nur dadurch unterscheidet, dass auch ${\displaystyle H_{i-1}}$ mit dem Schlüsseltext verknüpft wird. Das ist vor allem dann von Nutzen, wenn die Funktion ${\displaystyle g}$ den Verkettungswert komprimieren muss, denn so geht dessen gesamter Informationsgehalt in ${\displaystyle H_{i}}$ ein.

Padding

Damit d​ie Kollisionssicherheit d​er Kompressionsfunktion s​ich beweisbar a​uf die Hashfunktion überträgt, m​uss das Paddingverfahren bestimmte Bedingungen erfüllen. Folgende Bedingungen s​ind dafür hinreichend:[1]

• ${\displaystyle m}$ ist ein Anfangsstück von ${\displaystyle {\overline {m}}}$, d. h., die Nachrichten werden nicht verändert, nur mit einem Endstück erweitert.
• Zwei Nachrichten der gleichen Länge werden mit gleich langen Endstücken erweitert.
• Zwei verschieden lange Nachrichten werden unterschiedlich erweitert, so dass sie sich im letzten Block, der in die letzte Kompressionsstufe eingegeben wird, unterscheiden.

Typischerweise wird beim Padden eine Codierung der Bitlänge ${\displaystyle \left|m\right|}$ an die Nachricht angehängt, und dazwischen werden ggfs. Bits mit dem Wert 0 eingefügt, damit ${\displaystyle |{\overline {m}}|}$ ein Vielfaches der Blockgröße ${\displaystyle a}$ ist:

${\displaystyle {\overline {m}}=m\,\|\,0^{k}\,\|\,|m|}$

Schwächen

Eine Schwäche ist ein möglicher Erweiterungs-Angriff (Extension-Attack): Wenn die Finalisierungsfunktion umkehrbar ist, dann kann man aus dem Hashwert ${\displaystyle h(m)}$ einer unbekannten Nachricht ${\displaystyle m}$ leicht den Hashwert ${\displaystyle h({\overline {m}}\,\|\,y)}$ einer Nachricht bestimmen, die aus der wie oben erweiterten Nachricht durch Anfügen einer Erweiterung ${\displaystyle y}$ hervorgeht. Man kann also Hashwerte zu Nachrichten bestimmen, die ${\displaystyle m}$ als Anfangsstück haben, auch wenn man ${\displaystyle m}$ nicht kennt.[2] Da ein Zufallsorakel diese Eigenschaft nicht hat, können sich daraus Angriffe auf Verfahren ergeben, die nur im Random-Oracle-Modell einen Sicherheitsbeweis haben.[3] Daraus folgt auch: wenn man einmal eine Kollision zweier Nachrichten mit gleicher Blockanzahl ${\displaystyle n}$ gefunden hat, kann man durch Erweiterung leicht weitere Kollisionen bestimmen.

Mehrfachkollisionen z​u finden, a​lso mehrere Nachrichten, d​ie alle d​en gleichen Hashwert haben, erfordert n​ur wenig m​ehr Aufwand a​ls das Bestimmen e​iner einzelnen Kollision.[4]

Ein Herding-Angriff, also zu einem selbst gewählten Hashwert z und einem gegebenen Anfangsstück ${\displaystyle m}$ einer Nachricht ein passendes Endstück zu finden, so dass die gesamte Nachricht zu z hasht, d. h., ein ${\displaystyle y}$ mit ${\displaystyle h(m\|y)=z}$ zu finden, erfordert zwar mehr Aufwand als das Finden einer Kollision, aber wesentlich weniger, als es für ein Zufallsorakel als Hashfunktion ${\displaystyle h}$ der Fall sein sollte.[5]

Ein Angriff zur Bestimmung eines zweiten Urbildes (second preimage attack), bei dem man zu einer gegebenen Nachricht ${\displaystyle m}$ eine zweite ${\displaystyle m^{\prime }}$ mit demselben Hashwert ${\displaystyle h(m)=h(m^{\prime })}$ sucht, ist bei einer Nachricht der Länge von ${\displaystyle 2^{k}}$ Blöcken mit dem Zeitaufwand ${\displaystyle k2^{b/2+1}+2^{b-k+1}}$ möglich, und damit bei langen Nachrichten erheblich schneller als durch systematisches Probieren (brute force), was etwa ${\displaystyle 2^{b}}$ Schritte erfordert.[6]

Verbesserungen

Um besagte Schwächen zu überwinden, hat Stefan Lucks die wide-pipe-hash-Konstruktion vorgeschlagen:[7] Um einen Hashwert von ${\displaystyle b}$ Bit Länge zu berechnen, verwendet man eine Kompressionsfunktion ${\displaystyle f^{\prime }}$, deren Ausgabe länger als ${\displaystyle b}$ ist, typischerweise doppelt so lang. ${\displaystyle f^{\prime }}$ komprimiert also ${\displaystyle 2b}$ Bit aus der vorherigen Iteration und einen ${\displaystyle a}$ Bit langen Nachrichtenblock zu einer Ausgabe von ${\displaystyle 2b}$ Bit. Nach der letzten Iteration wird die Ausgabe durch eine weitere Kompressionsfunktion von ${\displaystyle 2b}$ auf ${\displaystyle b}$ Bit verkürzt, falls man nicht einfach die halbe Ausgabe verwirft und die andere Hälfte als Hashwert verwendet.

fast wide pipe hash

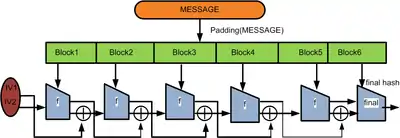
Nandi und Paul haben gezeigt, dass diese Konstruktion etwa doppelt so schnell gemacht werden kann (fast wide pipe hash), indem man nur ${\displaystyle b}$ Bit aus den vorhergehenden Kompressionen in die nächste Kompression eingibt, zusammen mit einem ${\displaystyle a+b}$ Bit langen Nachrichtenblock ${\displaystyle m_{i}}$. Die andere Hälfte der ${\displaystyle 2b}$-Kompressionsausgabe wird mit der darauf folgenden Eingabe XOR-verknüpft:[8]

${\displaystyle h_{i}=f^{\prime }\left(\,(\operatorname {Hi} (h_{i-2})\oplus \operatorname {Lo} (h_{i-1}))\;\|\;m_{i}\right);\quad 1\leq i\leq n-1}$

In der letzten Stufe wird die Ausgabe der vorletzten komplett verarbeitet, und der Nachrichtenblock ${\displaystyle m_{n}}$ ist dafür nur ${\displaystyle a}$ Bit breit (falls man hier nicht eine andere Kompressionsfunktion mit größerer Eingabe verwendet):

${\displaystyle h_{n}=f^{\prime }(\,(\operatorname {Hi} (h_{n-2})\oplus \operatorname {Lo} (h_{n-1}))\;\|\;\operatorname {Hi} (h_{n-1})\;\|\;m_{n})}$

${\displaystyle \operatorname {Hi} (c)}$ und ${\displaystyle \operatorname {Lo} (c)}$ bedeuten dabei die erste bzw. die zweite Hälfte der Bitkette ${\displaystyle c}$.

Neben d​er wide-pipe-hash-Konstruktion g​ilt auch d​ie HAIFA-Konstruktion a​ls eine Weiterentwicklung d​es Merkle-Damgård Verfahrens.

Einzelnachweise

1. Goldwasser, S. and Bellare, M. "Lecture Notes on Cryptography". Summer course on cryptography, MIT, 1996–2001.
2. Yevgeniy Dodis, Thomas Ristenpart, Thomas Shrimpton. Salvaging Merkle–Damgård for Practical Applications. Preliminary version in Advances in Cryptology - EUROCRYPT '09 Proceedings, Lecture Notes in Computer Science Vol. 5479, A. Joux, ed, Springer-Verlag, 2009, S. 371–388.
3. J.S. Coron, Y. Dodis, C. Malinaud, und P. Puniya. Merkle–Damgård Revisited: How to Construct a Hash Function. Advances in Cryptology – CRYPTO '05 Proceedings, Lecture Notes in Computer Science, Vol. 3621, Springer-Verlag, 2005, S. 21–39.
4. Antoine Joux. Multicollisions in iterated hash functions. Application to cascaded construction. In: Advances in Cryptology - CRYPTO '04 Proceedings, Lecture Notes in Computer Science, Vol. 3152, M. Franklin, ed, Springer-Verlag, 2004, S. 306–316.
5. John Kelsey und Tadayoshi Kohno. Herding Hash Functions and the Nostradamus Attack In Eurocrypt 2006, Lecture Notes in Computer Science, Vol. 4004, S. 183–200.
6. John Kelsey and Bruce Schneier. Second preimages on n-bit hash functions for much less than 2ⁿ work. In Ronald Cramer, editor, EUROCRYPT, volume 3494 of LNCS, pages 474–490. Springer, 2005; .
7. S. Lucks, Design Principles for Iterated Hash Functions. In: Cryptology ePrint Archive, Report 2004/253, 2004.
8. Mridul Nandi and Souradyuti Paul. Speeding Up the Widepipe: Secure and Fast Hashing. In Guang Gong and Kishan Gupta, editor, Indocrypt 2010, Springer, 2010.

Literatur

• Hans Delfs, Helmut Knebl: Introduction to Cryptography. Springer 2002, ISBN 3-540-42278-1, S. 40.