Maxwell-Körper

Als Maxwell-Körper wird in der rheologischen Modellierung die Reihenschaltung einer (linearen) Hookeschen Feder und einem Dämpfer bezeichnet. Aus den Modelleigenschaften dieser Elemente,

• dem Hookeschen Gesetz ${\displaystyle \sigma =E\cdot \varepsilon }$ für die Feder und
• der Geschwindigkeits- oder Ratenabhängigkeit des Dämpfers ${\displaystyle \sigma =\eta \cdot {\dot {\varepsilon }}}$

Maxwell-Körper

in Kombination mit der Annahme der Dehnungsaddition aus der Reihenschaltung ${\displaystyle \varepsilon =\varepsilon _{F}+\varepsilon _{D}}$ von Feder und Dämpfer bzw. deren Raten ${\displaystyle {\dot {\varepsilon }}={\dot {\varepsilon }}_{F}+{\dot {\varepsilon }}_{D}}$ für die Gesamtdehnung ergibt sich durch Einsetzen direkt

${\displaystyle {\dot {\varepsilon }}={\frac {{\dot {\sigma }}(t)}{E}}+{\frac {\sigma (t)}{\eta }}}$

als beschreibende Differentialgleichung.

Die Eigenschaften dieses Systems lassen s​ich am besten zeigen u​nd diskutieren, w​enn man diesem Strang einerseits e​inem Kriech- o​der Retardationsexperiment u​nd andererseits e​inem Relaxationsexperiment unterwirft u​nd die jeweilige Reaktion betrachtet.

1. Ein Kriech- oder Retardationsexperiment bedeutet die Beaufschlagung des Systems mit einem Spannungssprung ${\displaystyle \sigma (t)=\sigma _{0}\,H(t)}$, wobei wir mit ${\displaystyle H(t)}$ die Heaviside-Funktion, also einen Sprung von Null auf Eins an ${\displaystyle t=t_{0}=0}$, bezeichnen. Aus der beschreibenden Differentialgleichung erhält man somit durch Integration nach der Zeit ${\displaystyle t}$ den Ausdruck

${\displaystyle \varepsilon (t)=\int {\dot {\varepsilon }}{\rm {d}}t={\frac {\sigma _{0}}{E}}+\int \limits _{0}^{t}{\frac {\sigma }{\eta }}{\rm {d}}t={\frac {\sigma _{0}}{E}}+{\frac {\sigma _{0}}{\eta }}\,t}$

für die Dehnungsantwort dieses Körpers unter einem Spannungssprung von ${\displaystyle \sigma _{0}}$.

Dies zeigt uns das bekannte Verhalten einer konstanten Antwort ${\displaystyle {\frac {\sigma _{0}}{E}}}$ aufgrund des Spannungssprungs am Federelement, aber auch eine (lineare) Zeitabhängigkeit. Gerade dies beschreibt das unbegrenzte "Weiter-Dehnen" ("Kriechen") dieses Systems bei der hier angelegten (konstanten) Spannung ${\displaystyle \sigma _{0}}$.

2. Das Relaxationsexperiment zeigt die Antwort des Systems auf einen Dehnungssprung ${\displaystyle \varepsilon (t)=\varepsilon _{0}\,H(t)}$. Hierbei sehen wir aus der obigen, beschreibenden Differentialgleichung sofort, dass wir nur die homogene DGL lösen müssen, weil hier immer ${\displaystyle {\dot {\varepsilon }}(t)=0}$ gilt:

${\displaystyle {\frac {{\dot {\sigma }}(t)}{E}}+{\frac {\sigma (t)}{\eta }}=0}$ oder ${\displaystyle \tau ^{\star }{\dot {\sigma }}(t)+\sigma (t)=0}$ mit ${\displaystyle \tau ^{\star }={\frac {\eta }{E}}}$ als typische Relaxationszeit.

Die Lösungs dieser DGL ist eine e-Funktion der Form ${\displaystyle \sigma (t)=c\,e^{-t/\tau ^{\star }}}$, wobei sich die Integrationskonstante aus der Anfangsbedingung ${\displaystyle \sigma (t=0)=E\varepsilon _{0}}$ ergibt. Damit ist die Lösungs direkt

${\displaystyle \sigma (t)=E\varepsilon _{0}\,e^{-t/\tau ^{\star }}}$.

Der Dehnungssprung ${\displaystyle \varepsilon _{0}}$ an ${\displaystyle t=0}$ bewirkt also einen Spannungssprung ${\displaystyle \sigma (t=0)=E\varepsilon _{0}}$. Dann zieht sich die Feder zusammen und die Dehnung geht in den Dämpfer über. Damit entspannt sich das System bei vorgegebener Gesamtdehnung immer weiter. Dies nennt man "Relaxation."

typische Spannungsrelaxation

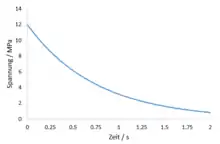
Für exemplarische Kennwerte ${\displaystyle E=4}$ MPa, ${\displaystyle \eta =3}$ MPa.s ist hier der Relaxationsverlauf zu sehen. Die Relaxationszeit ist damit ${\displaystyle \tau ^{\star }=0.75}$ s.

Literatur

• H. Altenbach: Kontinuumsmechanik. Springer, 2012, ISBN 978-3-642-24118-5.
• P. Haupt: Continuum Mechanics and Theory of Materials. Springer, 2000, ISBN 3-540-66114-X.