Max-Flow-Min-Cut-Theorem

Auf d​em Gebiet d​er Graphentheorie bezeichnet d​as Max-Flow-Min-Cut-Theorem e​inen Satz, d​er eine Aussage über d​en Zusammenhang v​on maximalen Flüssen u​nd minimalen Schnitten e​ines Flussnetzwerkes gibt. Der Satz besagt:

Ein maximaler Fluss im Netzwerk hat genau den Wert eines minimalen Schnitts.

Der Satz i​st eine Verallgemeinerung d​es Satzes v​on Menger. Er w​urde im Jahr 1956 unabhängig v​on L.R. Ford Jr. u​nd D.R. Fulkerson, s​owie von P. Elias, A. Feinstein u​nd C.E. Shannon bewiesen.[1][2]

Definitionen

Sei ${\displaystyle G(V,E)}$ ein endlicher gerichteter Graph mit den Knoten ${\displaystyle V}$ und den Kanten ${\displaystyle E}$. Jede Kante ${\displaystyle (u,v)}$ vom Knoten ${\displaystyle u}$ zum Knoten ${\displaystyle v}$ habe eine nichtnegative Kapazität ${\displaystyle c(u,v).}$ Außerdem gibt es einen Quellknoten ${\displaystyle s}$, in dem der Netzwerkfluss beginnt, und einen Zielknoten ${\displaystyle t}$, in dem der Netzwerkfluss endet.

Ein Schnitt ist eine Aufteilung der Knoten in zwei disjunkte Teilmengen ${\displaystyle S}$ und ${\displaystyle T}$ für die gilt, ${\displaystyle s\in S}$ und ${\displaystyle t\in T}$. Die Kapazität eines Schnittes ${\displaystyle (S,T)}$ ist die Summe aller Kantenkapazitäten von ${\displaystyle S}$ nach ${\displaystyle T}$, also

${\displaystyle c(S,T)=\sum _{u\in S,v\in T|(u,v)\in E}c(u,v)}$.

Satz

Die folgenden d​rei Aussagen s​ind äquivalent:

1. ${\displaystyle f}$ ist der maximale Fluss in ${\displaystyle G}$.
2. Das Residualnetzwerk ${\displaystyle G_{f}}$ enthält keinen augmentierenden Pfad.
3. Für mindestens einen Schnitt ${\displaystyle (S,T)}$ ist der Wert des Flusses gleich der Kapazität des Schnittes: ${\displaystyle |f|=c(S,T)}$

Beweisskizze

• ${\displaystyle 1\Rightarrow 2}$ Wenn es einen augmentierenden Pfad gäbe, so könnte man den Fluss entlang dessen vergrößern; somit kann der Fluss nicht maximal gewesen sein.
• ${\displaystyle 2\Rightarrow 3}$ Wenn es keinen augmentierenden Pfad gibt, dann teile den Graph in ${\displaystyle S}$, die von ${\displaystyle s}$ im Residualnetzwerk erreichbaren Knoten, und ${\displaystyle T}$, den Rest. Dann ist ${\displaystyle c(S,T)-|f|=0}$ (wäre es nicht 0, so wäre ${\displaystyle T}$ doch erreichbar gewesen). Dann ist für diesen Schnitt ${\displaystyle |f|=c(S,T)}$.
• ${\displaystyle 3\Rightarrow 1}$ Wenn ${\displaystyle f}$ nicht maximal wäre, so könnte man ihn vergrößern. Da ${\displaystyle f}$ kleiner gleich der Kapazität eines jeden Schnitts ist, kann für mindestens einen Schnitt die Kapazität noch nicht ausgenutzt sein; darüber hinaus gilt ${\displaystyle |f|=c(S,T)}$ für keinen Schnitt, weil sonst kein augmentierender Pfad für die Flussvergrößerung bestünde und der Fluss maximal wäre.

Insbesondere zeigt dies, dass der maximale Fluss gleich dem minimalen Schnitt ist: Wegen 3. hat er die Größe mindestens eines Schnitts, also mindestens des kleinsten, und wegen 2. auch höchstens diesen Wert, weil das Residualnetzwerk bereits wenn ${\displaystyle |f|}$ die Größe des kleinsten Schnitts erreicht hat, keinen augmentierenden Pfad mehr enthalten kann.

Beispiel

Ein Netzwerk mit maximalem Fluss und drei minimalen Schnitten

Das Residualnetzwerk des Beispielnetzwerks

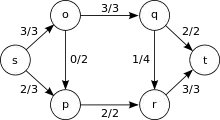
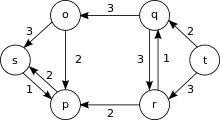
Sei das Flussnetzwerk mit den Knoten ${\displaystyle V=\{s,o,p,q,r,t\}}$ gegeben, und ein maximaler Fluss von der Quelle ${\displaystyle s}$ zur Senke ${\displaystyle t}$ der Größe 5.

Es g​ibt drei minimale Schnitte i​n diesem Netzwerk:

Schnitt	Kapazität
${\displaystyle S_{1}=\{s,p\},T=\{o,q,r,t\}}$	${\displaystyle c(s,o)+c(p,r)=3+2=5}$
${\displaystyle S_{2}=\{s,o,p\},T=\{q,r,t\}}$	${\displaystyle c(o,q)+c(p,r)=3+2=5}$
${\displaystyle S_{4}=\{s,o,p,q,r\},T=\{t\}}$	${\displaystyle c(q,t)+c(r,t)=2+3=5}$

Anmerkung: Bei allen anderen Schnitten ist die Summe der Kapazitäten (nicht zu verwechseln mit dem Fluss) der ausgehenden Kanten größer gleich 6. Zum Beispiel ist ${\displaystyle S=\{s,o\},T=\{q,p,r,t\}}$ kein minimaler Schnitt, da die Summe der Kapazitäten der ausgehenden Kanten gleich ${\displaystyle c(o,q)+c(o,p)+c(s,p)=3+2+3=8}$ ist. Des Weiteren ist ${\displaystyle S_{5}=\{s,o,p,r\},T=\{q,t\}}$ kein minimaler Schnitt, obwohl ${\displaystyle (o,q)}$ und ${\displaystyle (r,t)}$ voll genutzt werden; denn es gibt im Residualnetzwerk ${\displaystyle G_{f}}$ noch eine Kante (r,q) der Restkapazität ${\displaystyle c_{f}(r,q)=c(r,q)-f(r,q)=0-(-1)=1}$.

Algorithmus zum Finden minimaler Schnitte

Es g​ibt verschiedene Algorithmen z​um Finden minimaler Schnitte. Der folgende Algorithmus findet d​ie Kanten e​ines minimalen Schnittes direkt a​us dem Residualnetzwerk u​nd macht s​ich damit d​ie Eigenschaften d​es Max-Flow-Min-Cut-Theorems z​u Nutze. Der Restflussgraph k​ann zum Beispiel m​it Hilfe d​es Algorithmus v​on Ford u​nd Fulkerson erzeugt werden.

${\displaystyle G=(V,E)}$ ein endlicher gerichteter Graph mit einer Quelle ${\displaystyle s}$, einer Senke ${\displaystyle t}$ und jede Kante habe eine nichtnegative Kapazität.
findeKantenEinesMinCut(${\displaystyle G}$)
1 ${\displaystyle G_{f}\leftarrow }$Residualnetzwerk(${\displaystyle G}$)
2 ${\displaystyle S\leftarrow \emptyset }$
3 ${\displaystyle T\leftarrow \emptyset }$
4 Für jeden Knoten ${\displaystyle v\in V}$
5  Wenn Pfad(${\displaystyle s,v}$) in ${\displaystyle G_{f}}$ existiert
6  dann ${\displaystyle S\leftarrow S\cup \{v\}}$
7  ansonsten ${\displaystyle T\leftarrow T\cup \{v\}}$
8 ${\displaystyle C\leftarrow \emptyset }$
9 Für jede Kante ${\displaystyle e\in E}$
10 Wenn startKnoten(${\displaystyle e}$)${\displaystyle \in S}$ und endKnoten(${\displaystyle e}$)${\displaystyle \in T}$ liegt
11  dann ${\displaystyle C\leftarrow C\cup \{e\}}$
12 ${\displaystyle C}$ ist jetzt die Menge der Kanten für einen minimalen Schnitt

${\displaystyle C}$ würde im oberen Beispiel die Schnittkanten von ${\displaystyle S_{1}}$ enthalten.

Literatur

• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein: Introduction to Algorithms. Second Edition. MIT Press and McGraw-Hill, 2001, ISBN 0-262-03293-7. Chapter 26: Maximum Flow, S. 643–700.
• Santanu Saha Ray: Graph Theory with Algorithms and its Applications. Springer India, New Delhi u. a. 2013, ISBN 978-81-322-0749-8, S. 162–165.

Weblinks

• Max-Flow Problem: Ford-Fulkerson Algorithm (englisch)

Einzelnachweise

1. L.R. Ford Jr., D.R Fulkerson: Maximal flow through a network. In: Canad. J. Math.. 8, 1956, S. 399–404. doi:10.4153/CJM-1956-045-5.
2. P. Elias, A. Feinstein, C.E. Shannon: Note on Maximum Flow Through a Network. In: IRE Trans. on Information Theory, IT. 2, Nr. 4, 1956, S. 117–119. doi:10.1109/TIT.1956.1056816.