List Ranking

List Ranking bezeichnet die Aufgabe, den Elementen einer verketteten Liste ihren Rang innerhalb der Liste zuzuordnen. Der Rang eines Listenelements ist dabei definiert als der Abstand zum letzten Listenelement.

Das Ermitteln der Ränge ist notwendig, um Listen ohne den Verlust der Reihenfolge der Listenelemente in Arrays umzuwandeln, auf denen viele parallele Operationen effizienter ausgeführt werden können.[1] Der sequentielle Algorithmus zur Lösung der Aufgabe ist trivial mit einem Aufwand in $O(n)$ , parallele Algorithmen dagegen sind deutlich komplexer und schwieriger zu implementieren, erreichen dafür aber Laufzeiten von $O(\log n\log \log n)$ , wie beispielsweise der in diesem Artikel vorgestellte Independent-Set-Removal-Algorithmus.

Dieser Artikel beschränkt sich auf einfach verkettete Listen, außerdem soll das letzte Element einer Liste dadurch gekennzeichnet sein, dass es auf sich selbst als nächstes Element verweist.

Sequentieller Algorithmus für einfach verkettete Listen

Der sequentielle Algorithmus, auch unter dem Begriff Pointer Chasing bekannt, durchläuft die Liste einmal vom ersten Element bis zum letzten, und nummeriert die Elemente durch. In einem zweiten Durchlauf wird dann der Rang aus der Nummerierung und der Listenlänge bestimmt. Die Laufzeit für dieses Vorgehen ist in $O(n)$ , wobei $n$ die Länge der Liste bezeichnet (siehe: Landau-Symbole).

//Sei s das erste Element der Liste.
e := s
d := 0
e.rank := 0
while e.next != e
   e := e.next
   d := d + 1
   e.rank:= d
e := s
e.rank := d
while e.next != e
   e := e.next
   e.rank := d - e.rank

Parallele Algorithmen für List Ranking

Die parallelen Algorithmen für das List Ranking Problem werden im PRAM-Modell entworfen und analysiert. Um eine parallele Bearbeitung der Liste zu ermöglichen, muss angenommen werden, dass auf die Elemente der Liste bereits über ein Array zugegriffen werden kann, dabei enthält das Array aber keine Information über die Position der Listenelemente innerhalb der Liste.

Doubling

Der Doubling-Algorithmus ermittelt parallel für alle Listenelemente gleichzeitig ihren Rang, wobei aber im Gegensatz zum sequentiellen Algorithmus nicht für jedes Element die Liste über alle Elemente bis zum Ende durchlaufen wird, sondern Abkürzungen benutzt werden, die die Prozessoren gemeinsam erarbeiten.

//Seien e[i], i = 1,...,n, die Elemente der Liste.
//Auf Prozessoren p_1, ..., p_n parallel:
if e[p_i].next == e[p_i]
   e[p_i].rank := 0
else
   e[p_i].rank := 1
end if
while e[p_i].next.next != e[p_i].next
   e[p_i].rank := e[p_i].rank + e[p_i].next.rank
   e[p_i].next := e[p_i].next.next

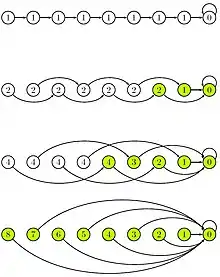
Beispiel für den Doubling Algorithmus

Die Abkürzungen werden in der letzten Zeile des Algorithmus aufgebaut, indem die Zeiger auf den jeweiligen Nachfolger der Elemente überschrieben werden durch Zeiger auf den Nachfolger des Nachfolgers. Die Längen dieser Abkürzungen werden in jeder Iteration, abgesehen von der letzten Iteration, immer verdoppelt. Zusätzlich zu der Abkürzung wird auch die Länge der Abkürzung gespeichert. Verweist die Abkürzung auf das letzte Listenelement, so ist die Länge der Abkürzung gerade der Rang des Listenelements.

Da durch die Verdopplung der Längen der Abkürzungen der Algorithmus für die Berechnung des Ranges des ersten Elements $\Theta (\log n)$ Schritte benötigt, ist auch die Gesamtlaufzeit des Algorithmus in $\Theta (\log n)$ . Die Effizienz des Algorithmus ist $1/\log n$ .

Der Algorithmus lässt sich auf allgemeine Prozessoranzahlen $p$ verallgemeinern, indem jedem Prozessor $n/p$ Elemente zugewiesen werden, die dieser dann bearbeitet. Die Laufzeit ist dann in $O({\frac {n}{p}}\log n)$ [2].

Independent Set Removal

Der Independent-Set-Removal-Algorithmus kann für beliebige Prozessoranzahlen verwendet werden und stellt eine Verbesserung gegenüber dem verallgemeinerten Doubling-Algorithmus dar.

Zunächst wird die Liste in aktive und inaktive Elemente unterteilt, der Doubling-Algorithmus wird dann nur auf die aktiven Elemente angewandt, daraufhin wird der Rang der inaktiven Elemente aus den bereits bekannten Rängen ermittelt. Damit hat der Independent-Set-Removal-Algorithmus den Vorteil, dass nicht mehr für jedes Element der Liste das Doubling ausgeführt werden muss.

Die Ränge werden wie beim Doubling-Algorithmus initialisiert:

//Seien e[i], i = 1, ..., n, die Elemente der Liste
//Auf Prozessoren p_1, ..., p_q parallel:
if e[i].next == e[i]
   e[i].rank := 0
else
   e[i].rank := 1
end if

Das Ziel ist es, in der Liste höchstens $m$ aktive Elemente auszuwählen, mit $m<n$ , und dann auf die aktiven Elemente das Doublingverfahren anzuwenden. Damit die verbleibenden Ränge bestimmt werden können, werden unabhängige Mengen benötigt:

Eine unabhängige Teilmenge $I$ der Listenelemente erfüllt die Eigenschaft: $e\in I\Rightarrow e.next\notin I$ . Für ein Element der unabhängigen Menge ist also der Nachfolger des Elements nicht in der unabhängigen Menge enthalten. Da der Nachfolger des letzten Elements es selbst ist, ist dieses nie in einer unabhängigen Menge enthalten. Wenn eine unabhängige Menge als inaktiv gekennzeichnet wird, so hat also jedes inaktive Element einen aktiven Nachfolger. Werden dann mittels Doubling die Ränge der aktiven Elemente bestimmt, so können die Ränge der inaktiven Elemente durch einfaches Abrufen des Rangs des aktiven Nachfolgers bestimmt werden.

Allerdings genügt es im Allgemeinen nicht, eine einzige unabhängige Menge zu bestimmen und als inaktiv zu kennzeichnen, um zu gewährleisten, dass höchstens $m$ Elemente aktiv sind: Benachbarte Elemente befinden sich nie in einer unabhängigen Teilmenge; demnach kann eine unabhängige Teilmenge höchstens die Hälfte der Listenelemente enthalten.

Es müssen wiederholt unabhängige Teilmengen aus der Liste entfernt werden, bis höchstens noch $m$ Elemente aktiv sind. Das Entfernen eines Elements ist vergleichbar mit dem Ermitteln einer Abkürzung im Doubling-Algorithmus: Die Länge der Abkürzung muss im Vorgänger des zu entfernenden Elementes gespeichert werden.

//Sei I eine unabhängige Menge.
//Für alle e[i] nicht in I parallel auf q Prozessoren:
if e[i].next enthalten in I
   //e[i].next soll aus der Liste entfernt werden
   e[i].rank := e[i].rank + e[i].next.rank
   e[i].next := e[i].next.next

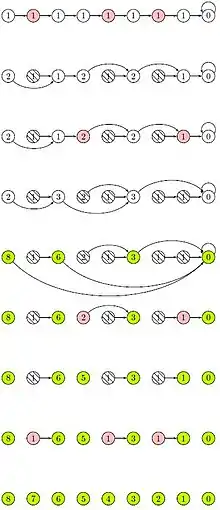
Beispiel für den Independent-Set-Removal-Algorithmus

Eine wichtige Beobachtung ist, dass alle aktiven Elemente den Abstand zum jeweiligen nächsten aktiven Element in ihrer rank-Variable speichern. Diese Eigenschaft bleibt bestehen, wenn wiederholt unabhängige Teilmengen entfernt werden.

Werden auf diese Weise rekursiv unabhängige Teilmengen entfernt, bis der Doubling-Algorithmus ausgeführt werden kann, so erhält man nach dessen Ausführung aktive Elemente, die ihren Rang kennen, und inaktive Elemente, die, als sie noch aktiv waren, ihren Abstand zum nächsten aktiven Element kannten. Fügt man nun die Teilmengen inaktiver Elemente in der umgekehrten Reihenfolge wieder in die Liste ein, in der sie entfernt wurden, so kennen diese Elemente weiterhin den Abstand zum jeweiligen nächsten aktiven Element, wodurch der Rang durch das Addieren des Abstands zum nächsten aktiven Element und dessen Rang bestimmt werden kann.

Um eine unabhängige Teilmenge zu bestimmen, kann wie folgt vorgegangen werden: Jedes Element der Liste wird mit Wahrscheinlichkeit $1/2$ als inaktiv markiert. Für jedes inaktive Element wird parallel geprüft, ob der Nachfolger ebenfalls inaktiv ist, und falls dem so ist, wird es als aktiv markiert. Die so gewonnene unabhängige Teilmenge enthält damit erwartet $1/4$ der gesamten Liste. Obwohl dieses Vorgehen ineffizient ist, übertrifft dieser Ansatz dennoch alle Alternativen aufgrund der äußerst geringen Kosten der einzelnen Operationen.[3]

Der vollständige Algorithmus:

Eingabe: Liste der Länge n
1. Initialisiere die Ränge
2. R := 0
   while mehr als m Elemente in der Liste
      R := R + 1
      Wähle eine unabhängige Teilmenge
      Entferne die unabhängige Teilmenge
3. Führe Doubling Algorithmus für die restlichen Elemente auf q Prozessoren aus
4. for i := R to 1
      Füge die Elemente ein, die bei Durchlauf i entfernt wurden
      Bestimme die Ränge der wieder hinzugefügten Elemente

Es kann gezeigt werden, dass mit $m=p$ , wobei hier $p$ nun die Anzahl Prozessoren bezeichne, für die erwartete Laufzeit gilt: $T(n,p)\in O({\frac {n}{p}}+\log {\frac {n}{p}}\log p)$ . Mit $p={\frac {n}{\log n\log \log n}}$ ergibt sich $T(n,p)\in O(\log n\log \log n)$ und eine Effizienz von 1.[4]

Jájá beweist in seinem Buch[5] für einen ähnlichen Algorithmus, in dem die unabhängige Menge deterministisch bestimmt wird, eine Laufzeit von $O(\log n\log \log n)$ , für die Wahl von $m=p=n/\log n$ , mit einer Effizienz von ${\frac {1}{\log \log n}}$ .

Außerhalb des PRAM-Modells

Die beschriebenen Algorithmen profitieren zum einen von der synchronisierten Ausführung im PRAM Modell, die bei realen Maschinen so nicht gegeben ist, und zum anderen vom globalen Speicher des PRAM-Modells. Auf realen Maschinen mit Verbindungsnetzwerk ist es allerdings sehr schwierig gute Resultate zu erhalten, da das List Ranking Problem eine in extremer Weise nicht lokale Aufgabe ist.[6] Damit ist gemeint, dass vorab nicht klar ist, welche Daten ein Prozessor aus dem Netzwerk anfordern muss, um dann lokal Arbeit zu verrichten, da erst durch das bearbeiten eines Listenelements klar wird, welches Element der Prozessor als nächstes benötigen wird, was viele langsame Zugriffe auf den Speicher nötig macht.

Einzelnachweise

Jop F. Sibeyn: Better Trade-offs for Parallel List Ranking. In: Proceedings of the ninth annual ACM symposium on Parallel algorithms and architectures. 1997, S. 221–222.
Peter Sanders, Michael Ikkert, Tim Kieritz, Parallele Algorithmen. Vorlesungsskript zu Parallele Algorithmen am Karlsruher Institut für Technologie. Abgerufen am 31. März 2019. S. 106.
Jop F. Sibeyn, Frank Guillaume, Tillmann Seidel: Practical Parallel List Ranking. In: Journal of Parallel and Distributed Computing. Volume 56, Issue 2, 1999, S. 162.
Peter Sanders, Michael Ikkert, Tim Kieritz, Parallele Algorithmen. Vorlesungsskript zu Parallele Algorithmen am Karlsruher Institut für Technologie. Abgerufen am 31. März 2019. S. 107+108.
J. Jájá: An Introduction to Parallel Algorithms. 1992, S. 97.
Jop F. Sibeyn, Frank Guillaume, Tillmann Seidel: Practical Parallel List Ranking. In: Journal of Parallel and Distributed Computing. Volume 56, Issue 2, 1999, S. 157.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Jop F. Sibeyn: Better Trade-offs for Parallel List Ranking. In: Proceedings of the ninth annual ACM symposium on Parallel algorithms and architectures. 1997, S. 221–222.

[2] Peter Sanders, Michael Ikkert, Tim Kieritz, Parallele Algorithmen. Vorlesungsskript zu Parallele Algorithmen am Karlsruher Institut für Technologie. Abgerufen am 31. März 2019. S. 106.

[3] Jop F. Sibeyn, Frank Guillaume, Tillmann Seidel: Practical Parallel List Ranking. In: Journal of Parallel and Distributed Computing. Volume 56, Issue 2, 1999, S. 162.

[4] Peter Sanders, Michael Ikkert, Tim Kieritz, Parallele Algorithmen. Vorlesungsskript zu Parallele Algorithmen am Karlsruher Institut für Technologie. Abgerufen am 31. März 2019. S. 107+108.

[5] J. Jájá: An Introduction to Parallel Algorithms. 1992, S. 97.

[6] Jop F. Sibeyn, Frank Guillaume, Tillmann Seidel: Practical Parallel List Ranking. In: Journal of Parallel and Distributed Computing. Volume 56, Issue 2, 1999, S. 157.