Liskovsches Substitutionsprinzip
Das Liskovsche Substitutionsprinzip (LSP) oder Ersetzbarkeitsprinzip ist ein Kriterium in der objektorientierten Programmierung, das die Bedingungen zur Modellierung eines Datentyps für seinen Untertyp angibt. Es besagt, dass ein Programm, das Objekte einer Basisklasse T verwendet, auch mit Objekten der davon abgeleiteten Klasse S korrekt funktionieren muss, ohne dabei das Programm zu verändern.
Das Liskovsche Substitutionsprinzip wurde erstmals 1987 von Barbara Liskov auf einer Konferenz Data abstraction and hierarchy vorgestellt und wurde 1993 von Barbara Liskov und Jeannette Wing formuliert.[1] In einem nachfolgenden Artikel wurde es folgendermaßen formuliert (Übersetzung):
„Eine stärkere Forderung [als Kovarianz und Kontravarianz] wird benötigt, die das Verhalten von Untertypen einschränkt: Eigenschaften, die anhand der Spezifikation des vermeintlichen Typs eines Objektes bewiesen werden können, sollten auch dann gelten, wenn das Objekt einem Untertyp dieses Typs angehört:
- Sei eine beweisbare Eigenschaft von Objekten des Typs . Dann soll für Objekte des Typs wahr sein, wobei ein Untertyp von ist.“[2]
Damit ist garantiert, dass Operationen, die auf ein Objekt des Typs vom Typ angewendet werden, auch korrekt ausgeführt werden. In einigen der heute üblichen Programmiersprachen, die Polymorphie unterstützen, kann dieses Prinzip durch Vererbung von mehr als einem Objekt auf ein anderes verletzt werden. Dann ließe sich nicht stets bedenkenlos ein Objekt vom Typ durch ein Objekt vom Typ ersetzen.
Bezogen auf einzelne Methoden bedeutet das Liskovsche Substitutionsprinzip, dass beim Überschreiben einer Methode durch eine abgeleitete Klasse die Vorbedingungen nur abgeschwächt und die Nachbedingungen nur verstärkt werden dürfen (siehe Design by Contract).
Das Problem
Ein wichtiges Element objektorientierter Programmierung ist die Vererbung: Eine Klasse (die Unterklasse) wird von einer anderen Klasse (ihrer Oberklasse) abgeleitet und erbt dabei ihre Methoden und Datenelemente. Dabei können neue Datenelemente hinzugefügt sowie Methoden hinzugefügt oder ersetzt werden.
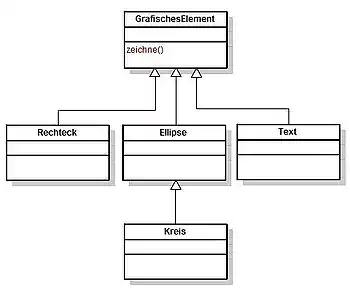
Dies führt zur Frage, was Vererbung über die Beziehung der Oberklasse zur Unterklasse aussagt. Diese Frage wird normalerweise beantwortet mit: Vererbung beschreibt eine ist-ein-Beziehung. Eine typische Hierarchie von Klassen in einem Grafikprogramm könnte z. B. aus einer Oberklasse GrafischesElement und davon abgeleiteten Unterklassen wie Rechteck, Ellipse oder Text bestehen. Beispielsweise wird man die Ableitung der Klasse Ellipse von der Klasse GrafischesElement begründen mit: Eine Ellipse ist ein grafisches Element. Die Klasse GrafischesElement kann dann beispielsweise eine allgemeine Methode zeichne definieren, die von Ellipse ersetzt wird durch eine Methode, die speziell eine Ellipse zeichnet.
Das Problem hierbei ist jedoch, dass das „ist-ein-Kriterium“ manchmal in die Irre führt. Wird für das Grafikprogramm beispielsweise die Klasse Kreis definiert, so würde man bei naiver Anwendung des „ist-ein-Kriteriums“ diese Klasse von Ellipse ableiten, denn ein Kreis ist eine Ellipse, nämlich eine Ellipse mit gleich langen Halbachsen. Diese Ableitung kann jedoch im Kontext des Grafikprogramms falsch sein: Grafikprogramme erlauben es üblicherweise, die grafischen Elemente zu verändern. Beispielsweise lässt sich bei Ellipsen die Länge der beiden Halbachsen unabhängig voneinander ändern. Für einen Kreis gilt dies jedoch nicht, denn nach einer solchen Änderung wäre er kein Kreis mehr. Hat also die Klasse Ellipse die Methoden SkaliereX und SkaliereY, so würde die Klasse Kreis diese Methoden erben, obwohl ihre Anwendung für einen Kreis nicht erlaubt ist.
Das Liskovsche Substitutionsprinzip deckt hier das Problem auf. Im vorliegenden Fall würde festgestellt, dass die Aussage „die Achsen können unabhängig voneinander skaliert werden“ zwar für die Klasse Ellipse, jedoch nicht für die Klasse Kreis gilt. Wäre jedoch Kreis eine Unterklasse von Ellipse, so müsste nach dem Liskovschen Substitutionsprinzip diese Aussage auch für die Klasse Kreis gelten. Daher ist Kreis hier keine Unterklasse von Ellipse.
Zu beachten ist hierbei, dass die Entscheidung jeweils abhängig vom konkreten Fall ist. Ist beispielsweise eine Manipulation der geometrischen Figur nach der Erzeugung nicht vorgesehen, so kann Kreis durchaus von Ellipse abgeleitet sein: Dass die Achsen unabhängig voneinander skaliert werden können, ist dann keine Eigenschaft der Klasse Ellipse, und somit muss sie auch keine Eigenschaft von Kreis sein, um Kreis zur Unterklasse von Ellipse zu machen.
Das Kreis-Ellipse-Problem als C#-Code:
public class GrafischesElement {
public virtual void Zeichne() {
// Code zum Zeichnen des Elements...
}
}
public class Ellipse : GrafischesElement {
public override void Zeichne() {
// Code zum Zeichnen der Ellipse...
}
public void SkaliereX(double pX) {
// Code zum Skalieren der X Achse...
}
public void SkaliereY(double pY) {
// Code zum Skalieren der Y Achse...
}
}
public class Kreis : Ellipse {
/** SkaliereR sollte statt SkaliereX/SkaliereY aufgerufen werden. */
public void SkaliereR(double pR) {
SkaliereX(pR * 2);
SkaliereY(pR * 2);
}
}
public void ZeichenBrett() {
public double X { get; set; }
public double Y { get; set; }
// Noch mehr Eigenschaften...
private List<GrafischesElement> ListeGrafischeElemente { get; set; }
// Noch mehr Variablen...
public void Aktualisiere(){
foreach(GrafischesElement gElem in ListeGrafischeElemente) {
if (gElem is Ellipse) {
var ellipse = gElem as Ellipse;
ellipse.SkaliereX(this.X); // <-- Kreis erbt von Ellipse! Kreis IST eine Ellipse!
ellipse.SkaliereY(this.Y); // <-- Kreis erbt von Ellipse! Kreis IST eine Ellipse!
}
// Noch mehr Code zum Neu-Zeichnen andere grafische Elemente...
}
}
}
Einzelnachweise
- Barbara H. Liskov, Jeannette M. Wing: Family Values: A Behavioral Notion of Subtyping. Pittsburgh 1993.(PostScript)
- Barbara H. Liskov, Jeannette M. Wing: Behavioral Subtyping Using Invariants and Constraints. Pittsburgh 1999 (PostScript).