Limesmenge

In d​er Theorie dynamischer Systeme bezeichnet m​an als Limesmengen (oder Grenzwertmenge) diejenigen Punkte d​es Zustandsraums, d​enen sich Orbits (für positive o​der negative Zeit) unendlich o​ft annähern.

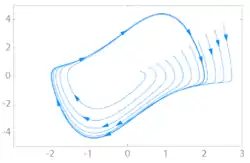
${\displaystyle \omega }$-Limesmenge (Grenzzyklus) des Van-der-Pol-Oszillators

Definition

Sei ${\displaystyle (T,X,\Phi )}$ ein dynamisches System mit ${\displaystyle T=\mathbb {Z} }$ (diskret) oder ${\displaystyle T=\mathbb {R} }$ (kontinuierlich). T ist meist die Zeit und X der Zustandsraum. Sei ${\displaystyle x\in X}$ ein Punkt des Zustandsraumes.

Die ${\displaystyle \omega }$-Limesmenge von ${\displaystyle x}$ ist

${\displaystyle \omega (x,\Phi ):=\left\{y\in X:\exists t_{n}\rightarrow \infty ,\Phi (t_{n},x)\rightarrow y\right\}}$.

Die ${\displaystyle \alpha }$-Limesmenge von ${\displaystyle x}$ ist

${\displaystyle \alpha (x,\Phi ):=\left\{y\in X:\exists t_{n}\rightarrow -\infty ,\Phi (t_{n},x)\rightarrow y\right\}}$.

Alternativ lassen s​ich Limesmengen a​uch wie f​olgt charakterisieren:

${\displaystyle \omega (x,\Phi )=\bigcap _{n\in T}{\overline {\left\{\Phi (t,x):t>n\right\}}}}$,

${\displaystyle \alpha (x,\Phi )=\bigcap _{n\in T}{\overline {\left\{\Phi (t,x):t<n\right\}}}}$.

Die Limesmengen sind abgeschlossen und invariant unter ${\displaystyle \Phi }$. Falls ${\displaystyle X}$ kompakt ist, sind die Limesmengen nicht leer.

Typen

• Fixpunkt
• Periodischer Orbit
• Grenzzyklus
• Seltsamer Attraktor

Literatur

• Gerald Teschl: Ordinary Differential Equations and Dynamical Systems (= Graduate Studies in Mathematics. Band 140). American Mathematical Society, Providence 2012, ISBN 978-0-8218-8328-0 (mat.univie.ac.at).