Leiterspiel
Das Leiterspiel oder auch Schlangen und Leitern (auf Englisch: Snakes and Ladders, in der Schweiz: Leiterlispiel; manchmal auch Lustiges Leiterspiel) bezeichnet eine Familie von Brettspielen, die dem traditionellen indischen Spiel Moksha Patamu nachempfunden wurden. Hatte Moksha Patamu noch eine religiöse Bedeutung, so ist diese in den westlichen Versionen gänzlich verschwunden.[1] Heute ist es in zahlreichen Varianten vor allem als Kinderspiel verbreitet.

Spielprinzip
Ein Leiterspiel-Spielplan enthält eine Kette von Spielfeldern, die von einem Start- zu einem Zielfeld führt und sich spiralförmig oder im Zickzack windet. An mehreren Stellen sind zwei nicht direkt aufeinanderfolgende Felder durch Schlangen, Leitern oder andere Zeichnungen verbunden.
Jeder Spieler beginnt mit einer Spielfigur auf dem Startfeld. Üblicherweise wird reihum ein einzelner Würfel geworfen. Dessen Ergebnis gibt an, wie viele Felder sich die Spielfigur vorwärtsbewegen darf. Endet ihr Zug auf dem Anfangsfeld einer Leiter, wird sie auf deren Endfeld vorgesetzt. Endet er auf einer Schlange, wird sie auf deren Endfeld versetzt, das wieder näher am Anfangsfeld liegt. Sieger ist, wer zuerst das Zielfeld erreicht.
Im Detail gibt es verschiedene Regeln zum punktgenauen Erreichen des Zielfeldes oder der Situation, dass das Endfeld einer Bewegung bereits von einer anderen Figur besetzt ist.
Varianten
Das Spiel ist in seiner Grundform ein reines Glücksspiel ohne strategische Elemente, weshalb es vor allem von und mit jüngeren Kindern gespielt wird. In der englischsprachigen Welt sind die ursprünglichen Leitern und Schlangen als Bilder auf dem Brett weit verbreitet geblieben, was vermutlich auf den immer noch gebräuchlichen Namen Snakes and Ladders zurückgeht. Im deutschen Sprachraum gibt es dagegen seltener Schlangen, sondern eher Alternativen wie Rutschen. Es gibt zahllose Varianten des Spielplanes mit unterschiedlicher Bahnlänge, Abkürzungszahl und -positionierung und zeichnerischer Gestaltung, oft mit bunten Hintergründen und thematisch angepassten Abkürzungen.
Das Grundprinzip des Spiels wird auch oft abgewandelt, indem etwa jeder Spieler mehrere Spielfiguren erhält oder einzelnen Feldern Spezialereignisse zugewiesen werden (rücke 3 Felder vor, setze eine Runde aus...). Das Leiterspiel ist auch eine beliebte Grundlage für Lernspiele, die einen thematischen Hintergrund setzen oder Wissensfragen einbauen. Meyer et al. (2020) explorierten auf der Basis des Leiterspiels mit einem freien und adaptiven Spiel-Projekt.[2] Dieses bezieht sich einerseits auf die systemische Spielpädagogik.[3] Die Spielenden entwickeln das Spiel von Grund auf selbst und legen die Regeln fest. Das zweite Element des Monza-Projekts ist die Mathematisierung. Während mehrerer Jahre abstrahieren Lehrpersonen und Lernende die Spielerfahrungen in die Sprache der Mathematik.
Geschichte
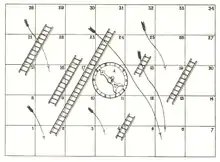
Das erste westliche Leiterspiel wurde 1892 von der Spielzeugfirma von Frederick Henry Ayres in England mit einem kreisförmigen Spielbrett auf den Markt gebracht. Im Uhrzeigersinn mussten die Spielfiguren bis in die Mitte gezogen werden. Das Spiel hatte insgesamt 100 Felder, auf denen fünf Schlangen und fünf Leitern eingezeichnet waren.[1]
R. H. Harte entwickelte 1893 eine Variante auf einem rechteckigen Spielfeld. Aus dem gleichen Jahr stammt ein Patent eines ähnlichen rechteckigen Spielbrettes, das nur noch 34 Einzelfelder beinhaltete.[4]

Um 1920 erschien bei Spear & Söhne ein Spiel mit dem Namen „Auf und Ab! Lustiges Leiterspiel“. Auf dem Brett befanden sich hier keine Schlangen mehr, sondern Zirkusszenen mit derselben Funktion.[1]
Mathematische Analyse
Bei den Standardregeln des Leiterspiels gibt es weder Entscheidungsmöglichkeiten der Spieler, noch eine Interaktion zwischen den Spielern. Daher kann die durchschnittliche Anzahl der Würfe, die bis zum Erreichen des Ziels notwendig ist, empirisch in einer Versuchsreihe eines einzelnen Spielers ermittelt werden. Für die von der Firma Milton Bradley vertriebene Version wurden 1960 die Ergebnisse einer Monte-Carlo-Simulation veröffentlicht.[5] Dabei ergab sich bei 16.384 Versuchen ein Durchschnitt von 39,420 Würfen bis zum Ziel.
In der genannten Veröffentlichung wird auch der Weg beschrieben, das genannte Ergebnis ohne Simulation im Rahmen einer Berechnung zu erhalten. Dazu wird das Leiterspiel durch eine absorbierende Markow-Kette mit 100 Zuständen, die zu den Spielfeldern korrespondieren, modelliert. Auf dieser Basis wird der Erwartungswert 39,224 der notwendigen Anzahl von Würfen berechnet.[6]
Siehe auch
Weblinks
Einzelnachweise
- Erwin Glonnegger: Das Spiele-Buch. Ravensburger Buchverlag, Ravensburg 1988, ISBN 3-473-42601-6
- Meyer, S. L., Rickenbacher, L. & Zürcher, E. (2020).Monza - Gesellschaftsspiel. HfHnews, (25) / Zürich. Verfügbar unter: https://www.researchgate.net/publication/344348618_Monza_-_Gesellschaftsspiel
- Heimlich, U. (2015).: Einführung in die Spielpädagogik (3., aktualisierte und erweiterte Auflage.). Bad Heilbrunn: Verlag Julius Klinkhard, ISBN 978-3825241995
- David Parlett: The Oxford History of Board Games. Oxford / New York 1999, ISBN 0-19-212998-8
- N. W. Bazley, P. J. Davis: Accuracy of Monte Carlo methods in computing finite Markov chains. In: Journal of Research of the National Bureau of Standards – Mathematics and Mathematical Physics, Band B64, 1960, S. 211–215. Die spezielle Version des untersuchten Spielplans findet man auf einem Foto in der englischen Wikipedia.
- Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel – Methoden, Ergebnisse und Grenzen, 7. Auflage, Springer Spektrum, 2018, ISBN 978-3-658-21764-8, S. 68–69, 75, doi:10.1007/978-3-658-21765-5. S. C. Althoen, L. King, K. Schilling: How long is a game of Snakes and Ladders? In: The Mathematical Gazette, Band 77, Nr. 478, March 1993, S. 71–76, doi:10.2307/3619261.