Kugelstoßpendel

Ein Kugelstoßpendel, auch Kugelpendel, Newtonpendel oder Newton-Wiege genannt, ist eine Anordnung von identischen elastischen Kugeln (meist aus Metall), die je an zwei (bifilar) gleichen Fäden in einer Reihe aufgehängt sind. Jede Kugel bildet ein Pendel gleicher Masse und Pendellänge und vorgegebenem Bewegungspfad. Der Abstand der Aufhängepunkte im Rahmen ist gleich dem Durchmesser der Kugeln, sodass diese in Ruhe senkrecht hängen und sich gerade berühren.

Ein Kugelstoßpendel veranschaulicht den elastischen Stoß

Wenn eine der äußeren Kugeln seitlich mit gestreckten Fäden abgehoben wird und gegen die Reihe der anderen Kugeln zurückfällt, bewirkt der Anprall, dass genau eine Kugel gegenüberliegend abgestoßen wird, während die anderen Kugeln in Ruhe bleiben. Pendelt diese Kugel zurück und prallt auf, wird durch den Stoß wieder die äußerste Kugel auf der anderen Seite abgestoßen – das System „schwingt“.

Bemerkenswert ist das Verhalten bei mehr als einer bewegten Kugel. Wenn zwei oder mehrere Kugeln an die verbleibenden Kugeln prallen, werden auf der anderen Seite immer ebensoviele Kugeln abgestoßen, wie sie auf der Gegenseite aufgeprallt sind – und nicht etwa nur eine einzelne Kugel mit höherer Geschwindigkeit, wie man vielleicht vermuten könnte.

Die Vorrichtung geht auf den französischen Physiker Edme Mariotte zurück, der sie erstmals 1673 in seinem Werk Traitté de la percussion ou chocq des corps veröffentlichte. Sie verbreitete sich ab den 1960er Jahren als kleines, dekoratives Spielzeug.

Physikalische Erklärung

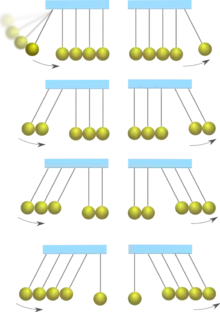
vor dem Stoß		nach dem Stoß

Varianten mit fünf Kugeln

Oft wird vermutet, dass eine Erklärung des Verhaltens vollständig durch Impuls- und Energieerhalt möglich sei. Jedoch bieten beide Sätze im Falle von 5 Kugeln gleicher Masse ( $m$ ) – davon eine zum Anstoß mit Geschwindigkeit ( $v_{1}$ ) benutzt und vier Kugeln anfänglich ruhend – lediglich zwei Gleichungen mit 5 Unbekannten ( $v_{1}',v_{2}',v_{3}',v_{4}',v_{5}'$ ):

mv_{1}=mv_{1}'+mv_{2}'+mv_{3}'+mv_{4}'+mv_{5}'

{\frac {m}{2}}v_{1}^{2}={\frac {m}{2}}v_{1}'^{2}+{\frac {m}{2}}v_{2}'^{2}+{\frac {m}{2}}v_{3}'^{2}+{\frac {m}{2}}v_{4}'^{2}+{\frac {m}{2}}v_{5}'^{2}

Mit den Geschwindigkeiten $v,v'$ vor bzw. nach dem Stoß der jeweiligen Kugeln. So wäre nach diesen Gleichungen auch eine Lösung im Einklang mit den Erhaltungssätzen möglich in der nach den Stößen zwei Kugeln abheben und die erste Kugel einen Rückstoß erfährt. Dies ist beispielsweise der Fall wenn die Kugeln vier und fünf miteinander verklebt werden (zusätzliche Bedingung $v_{4}'=v_{5}'$ ).

Bezieht man jedoch die zeitliche Abfolge in die Betrachtung ein, kann man zusätzliche Annahmen treffen: Die im nebenstehenden Bild am weitesten links liegende, ruhende Kugel nimmt den Impuls der aufprallenden Kugel auf und gibt ihn an die rechts daneben liegende Kugel ab, und die dann an die rechts daneben und so weiter. Dabei handelt es sich um eine schnelle Abfolge elastischer Stöße zwischen jeweils nur zwei Kugeln gleicher Masse. Die am weitesten rechts liegende Kugel kann allerdings keinen Impuls mehr weitergeben und wird abgestoßen. Werden zwei Kugeln für den Anstoß benutzt, pflanzt sich zunächst der zuerst eintreffende Impuls von Kugel zwei auf Kugel drei fort, bevor Kugel eins an Kugel zwei weitergibt, und so weiter.

Diese zeitliche Abfolge wurde 2014 durch Kristof Heck und Simon Huppertz bei „Jugend forscht“ (2. Bundessieger) und in den 90er Jahren von Prof. Albrecht Böhm im Rahmen von Vorlesungen zur Experimentalphysik an der RWTH Aachen mittels eines Piezo-Sensors zwischen den Kugeln untersucht und bestätigt.[1]

Die einzelnen Stöße gleicher Kugeln mit Masse $m$ pflanzen ihren Impuls sowie ihre kinetische Energie vollständig auf die jeweils nächste Kugel fort, wie sich für dieses vereinfachte System mit nur zwei Kugeln mittel Impuls- und Energieerhalt zeigen lässt:

mv_{1}=mv_{1}'+mv_{2}'

und

{\frac {m}{2}}v_{1}^{2}={\frac {m}{2}}v_{1}'^{2}+{\frac {m}{2}}v_{2}'^{2}

v_{1}-v_{2}'=v_{1}'

und

v_{1}^{2}=v_{1}'^{2}+v_{2}'^{2}

v_{1}^{2}=(v_{1}-v_{2}')^{2}+v_{2}'^{2}

0=-2v_{1}v_{2}'+2v_{2}'^{2}

Die Lösungen dieser quadratischen Gleichung (und eingesetzt in die zweite Zeile) sind $v_{1}'=v_{1}$ und $v_{2}'=0$ (zu einem Zeitpunkt vor dem Stoß) sowie $v_{1}'=0$ und $v_{2}'=v_{1}$ (nach dem Stoß).

Literatur

F. Herrmann, P. Schmälzle: Simple explanation of a well-known collision experiment. In: Am. J. Phys. Band 49, 1981, S. 761 ff. ( [PDF; 295 kB]).
F. Herrmann, M. Seitz: How does the ball-chain work? In: Am. J. Phys. Band 50, 1982, S. 977 ff. (oebv.at (Memento vom 24. Dezember 2012 im Internet Archive) [PDF; 360 kB]).

Weblinks

Commons: Kugelstoßpendel – Album mit Bildern und Videos

Wiktionary: Kugelstoßpendel – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Einzelnachweise

Kristof Heck, Simon Huppertz: Jugend-forscht 2014, Physik: Untersuchungen zur Kugelstoß-Pendelkette und zur Hertzschen Kontakt-Theorie. (mgm-monschau.de9 [PDF; 3,3 MB; abgerufen am 29. Dezember 2016]).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Kristof Heck, Simon Huppertz: Jugend-forscht 2014, Physik: Untersuchungen zur Kugelstoß-Pendelkette und zur Hertzschen Kontakt-Theorie. (mgm-monschau.de9 [PDF; 3,3 MB; abgerufen am 29. Dezember 2016]).