Kreisbogengraph

Ein Kreisbogengraph ist in der Diskreten Mathematik eine Struktur der Graphentheorie.

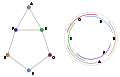Links ein Kreisbogengraph und rechts ein Modell dafür
Die dargestellte Biklaue ist ein Beispiel für einen einfachen Graphen, der kein Kreisbogenmodell besitzt.

Sei $G=(V,E)$ ein Graph. Ist ${\mathcal {K}}:=\{K_{x}\}_{x\in V}$ eine Familie von Kreisbögen zu einem festen Radius dergestalt, dass gilt

{\begin{aligned}K_{x}\cap K_{y}\neq \emptyset \Leftrightarrow (x,y)\in E,\end{aligned}}

so heißt ${\mathcal {K}}$ Kreisbogenmodell für $G$ . Ein Graph ist genau dann ein Kreisbogengraph, wenn er ein Kreisbogenmodell besitzt. Kreisbogengraphen wurden ab den 1970er Jahren zuerst von Alan Tucker und dann bald von vielen Weiteren untersucht.

Einige Teilklassen

Gibt es ein Modell mit der Eigenschaft, dass alle Kreisbögen Einheitslänge haben, spricht man von einem Unit-Kreisbogengraph. Lässt sich eine Familie angeben, in der alle Inklusionen von Kreisbögen echte Inklusionen sind, spricht man von Proper-Kreisbogengraphen. Existiert ein Modell so, dass die Kreisbögen als Mengen die Helly-Eigenschaft besitzen, heißt der Graph auch Helly-Kreisbogengraph.

Die Intervallgraphen sind ein wichtiger Spezialfall. Im Gegensatz zu diesen sind Kreisbogengraphen im Allgemeinen jedoch nicht mehr perfekt oder chordal, denn für ungerade Kreisgraphen existiert stets ein Kreisbogenmodell. Auch die lineare Beschränkung an die Anzahl maximaler Cliquen, die man bei Intervallgraphen hat, geht in eine exponentielle Schranke über.

Algorithmische Komplexität klassischer Probleme

	Kreisbogengraph
Erkennung	Linear (McConnel 2003)
3-Färbung	Polynomiell (Garey et al. 1980)
Cliquenüberdeckung	Linear (Hsu und Tsai 1991)
Unabhängige Menge	Linear (Hsu und Tsai 1991)
Dominierende Menge	Linear (Hsu und Tsai 1991)
Hamiltonpfad	Polynomiell (Mertizios und Bezák 2014)
Hamiltonkreis	Polynomiell (Shih et al. 1992)
Färbungszahl	NP-vollständig (Garey et al. 1980)

Literatur

Michael R. Garey, David S. Johnson, Gary L. Miller, Christos H. Papadimitriou: The complexity of coloring circular arcs and chords. In: SIAM Journal on Algebraic Discrete Methods. Band 1, Nr. 2, 1980, S. 216–227 (Online [PDF]).
Wen-Lian Hsu, Kuo-Hui Tsai: Linear time algorithms on circular-arc graphs. In: Information Processing Letters. Band 40, Nr. 3, 8. November 1991, ISSN 0020-0190, S. 123–129, doi:10.1016/0020-0190(91)90165-E (Online).
W. Shih, T. Chern, W. Hsu: An $O(n^2 \log n)$ Algorithm for the Hamiltonian Cycle Problem on Circular-Arc Graphs. In: SIAM Journal on Computing. Band 21, Nr. 6, 1. Dezember 1992, ISSN 0097-5397, S. 1026–1046, doi:10.1137/0221061 (Online).
George B. Mertzios, Ivona Bezáková: Computing and counting longest paths on circular-arc graphs in polynomial time. In: Discrete Applied Mathematics. 164, Part 2, 19. Februar 2014, ISSN 0166-218X, S. 383–399, doi:10.1016/j.dam.2012.08.024 (Online).
Ross M. McConnell: Linear-Time Recognition of Circular-Arc Graphs. In: Algorithmica. Band 37, Nr. 2, 14. Juli 2003, ISSN 0178-4617, S. 93–147, doi:10.1007/s00453-003-1032-7.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.