Korona (atmosphärische Optik)

Als Korona (lateinisch corona „Kranz, Krone“) oder Hof bezeichnet man eine Leuchterscheinung um Mond oder Sonne, die durch Beugung des Lichts an den Wassertröpfchen von Wolken verursacht wird – im Gegensatz zum Regenbogen oder zu Haloeffekten, die beide durch Brechung entstehen. Bei einer Korona ist oft nur eine weiße Scheibe mit rötlichem Rand zu sehen, die Aureole genannt wird. Unter günstigen Bedingungen ist die Aureole von mehreren farbigen Ringen umgeben.

Mondhof oder lunare Korona mit ringförmigen Interferenzerscheinungen (Farbtemperatur 4250 Kelvin). Bildhöhe und Bildbreite entsprechen einem Bildwinkel von knapp 8 Bogengrad.

Mond mit mehrfarbiger Korona im Goldenen Tor der Ekliptik bei leichter Bewölkung mit mehrfarbiger Korona (unten im Bild der Rote Riese Aldebaran, oben rechts die Plejaden). Die Farbe der Wolken ist im neutralen Grau (Farbtemperatur des Mondlichts = 4100 Kelvin).

Der Durchmesser der Aureole um Sonne oder Mond hat eine Winkelausdehnung zwischen 2,5° und 8°, der Winkeldurchmesser der äußeren Ringe kann bis zu 15° betragen. Der Beugungseffekt, der die Korona erzeugt, muss nicht notwendigerweise durch Wassertröpfchen verursacht werden. In seltenen Fällen können Eiskristalle oder andere Aerosole ebenfalls Koronen hervorrufen, beispielsweise bei einer Pollenkorona.

Eine solche Korona ist ein Effekt der Atmosphärischen Optik, im Gegensatz zur Sonnenkorona, bei der es sich um die nur bei einer totalen Sonnenfinsternis sichtbar werdende Atmosphäre der Sonne handelt.

Aussehen und Auftreten

Eine schwache Aureole um die aufgehende Sonne

Korona um eine Straßenlampe, erzeugt durch eine beschlagene Scheibe

Schieben sich Wolken vor Sonne oder Mond, bilden sich unter bestimmten Bedingungen leuchtende Scheiben um die jeweilige Lichtquelle, die manchmal noch von farbigen Ringen umgeben sind. Der wissenschaftliche Name für diese Leuchterscheinung ist Korona, die helle Scheibe im Zentrum der Korona heißt Aureole. In der Alltagssprache wird diese oft Hof und die farbigen Ringe auch Kränze genannt. Allerdings werden die Begriffe nicht immer in dieser Weise benutzt, und als weitere Quelle der Verwirrung werden in älteren Texten Halos ebenfalls als Kränze bezeichnet.

Koronen sind meist um den Mond zu beobachten, seltener um die Sonne. Dies liegt nicht daran, dass sie um die Sonne weniger häufig auftreten, sondern daran, dass das Licht der Sonne die Koronaerscheinung überstrahlt und man darüber hinaus in der Regel den Blick in die Sonne meidet (und wegen der Gefahr für die Augen auch meiden sollte). Zur Beobachtung von Sonnenkoronen muss das Sonnenlicht daher abgeschwächt werden – durch die Verwendung von Filtern oder indem man das Phänomen im Spiegelbild beobachtet, auf einem Gewässer oder einer Fensterscheibe. Bei günstigen Verhältnissen können auch Koronen um Planeten[1] oder Sterne[2] beobachtet werden.

Meist ist nur die Aureole um den Mond zu sehen – eine weiße Scheibe, deren Rand in Gelb und Rot übergeht. Der Mond selbst wird von der Aureole oftmals überstrahlt. Ist er zu sehen, fällt der Größenunterschied zwischen ihm und der Aureole sofort auf: Während die Scheibe des Vollmonds unter einem Sehwinkel von etwa 0,5° zu sehen ist, erreicht der Durchmesser der Aureole, abhängig von der Größe der Tropfen (siehe Einfluss der Tropfengröße), eine Winkelausdehnung von typischerweise 2,5° bis 8°. Aureolen kommen mehr oder weniger ausgeprägt in fast allen, nicht zu dicken Arten von Wolken vor, weshalb sie vergleichsweise häufig auftreten. Besonders oft erscheinen Koronen bei Altocumulus-Wolken und dünnen Schichtwolken.

Unter günstigen Bedingungen schließen sich an die Aureole farbige Ringe an (siehe Einfluss der Wellenlänge), wobei von innen nach außen die Farben Blau, Grün, Gelb und Rot zu sehen sind. Es wurden bis zu vier Ringsysteme beobachtet. Bei den äußeren fehlt das Blau, ansonsten sind die Farben ähnlich denen im innersten Ringsystem. Koronen können sehr unterschiedliche Ausdehnungen haben, der Winkeldurchmesser der äußersten Ringe kann bis zu 15° betragen. Beim Durchzug von Wolken kann sich die Korona verändern – der Durchmesser kann wachsen oder schrumpfen, Ringe erscheinen oder verschwinden wieder, je nachdem, wie sich die Tropfengrößen verändern.

Man kann außerdem künstliche Koronen beobachten oder erzeugen, indem man beispielsweise durch eine beschlagene Scheibe oder Nebel auf eine Lampe blickt.[3]

Entstehung

Die Korona als Beugungsbild

Zum Vergleich: Halo (oben), Korona (unten). Neben den intensiveren Farben bei der Korona ist vor allem der Größenunterschied auffällig.

Koronen sind eine Beugungserscheinung und dürfen nicht mit den Halos um Sonne oder Mond verwechselt werden – diese entstehen durch Brechung des Lichtes in Eiskörnern hoher Wolken und haben einen größeren Durchmesser (von meistens 22°, seltener auch 46°) sowie eine andere Farbreihenfolge. Koronen entstehen durch Beugung des Sonnen- oder Mondlichtes an Wassertropfen – es müssen also Wolken vorhanden sein, wenn man eine Korona beobachten will. Diese Wolken dürfen andererseits aber auch nicht zu mächtig sein, da das Mond- oder Sonnenlicht sie durchdringen können muss.

Licht ist eine elektromagnetische Welle. Um Beugungseffekte zu verstehen, reicht die einfache Strahlenoptik nicht mehr aus, sondern die Welleneigenschaften des Lichtes müssen berücksichtigt werden. Die Beugung der Lichtwellen an einem Hindernis lenkt das Licht aus seiner ursprünglichen Richtung ab. Überlagerungen der gebeugten Wellen können wiederum Interferenzerscheinungen hervorrufen, die sogenannten Beugungsbilder. Wie diese Beugungsbilder aussehen, hängt unter anderem von der Form des beugenden Gegenstandes ab. Wassertropfen sind kugelförmig und bilden daher für das sich ausbreitende Licht ein kreisförmiges Hindernis. Deshalb entspricht das Beugungsbild eines Wassertropfens annähernd dem einer Kreisscheibe. Dieses wiederum entspricht nach dem Babinetschen Theorem in guter Näherung demjenigen einer Kreisblende gleichen Durchmessers: einem hellen Scheibchen, dem Zentralbild mit der größten Intensität, und konzentrischen hellen und dunklen Ringen, wobei die Intensität der hellen Ringe nach außen abnimmt. Während das Zentralbild mehr oder weniger der ursprünglichen Ausbreitungsrichtung des Lichtes entspricht (der Ablenkwinkel liegt um 0°), haben die Ringe einen umso größeren Durchmesser, je größer der Ablenkwinkel ist. Der Durchmesser der Beugungsringe hängt vom Tropfendurchmesser und der Lichtwellenlänge ab. Die Ringe werden umso weiter, je größer die Wellenlänge ist und je kleiner die beugenden Wassertropfen in der Wolke sind.[3]

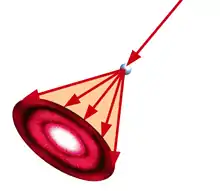
Die Beugungsringe sind die Schnittlinien der Kegelmäntel mit der Ebene des Schirms.

Die Beugungsbilder sämtlicher Wassertropfen einer Wolke werden von einem irdischen Beobachter als ein einziges System konzentrischer Ringe um die Lichtquelle wahrgenommen (der Korona), das dem Beugungsbild eines einzelnen Tropfens auf einem Schirm entspricht. Das kommt folgendermaßen zustande:

Das Beugungsbild eines einzelnen Tropfens auf einem Schirm – also in einer bestimmten Ebene senkrecht zur ursprünglichen Ausbreitungsrichtung des Lichtes – besteht aus konzentrischen Ringen. Diese Ringe sind die Schnittlinien der Kegelmäntel, in die das Licht hineingebeugt wird, mit der Ebene des Schirms. Zunächst erzeugt also jeder Tropfen sein eigenes Beugungsbild und seine eigenen Kegelmäntel gebeugten Lichtes. (In der Abbildung ist aus Gründen der Übersichtlichkeit nur ein Kegelmantel dargestellt; tatsächlich gehört zu jedem Beugungsring natürlich jeweils ein eigener Kegelmantel. Zu beachten ist dabei, dass es sich bei dem zentralen Beugungsscheibchen nicht um einen Kegelmantel, sondern um einen Kegel handelt.)

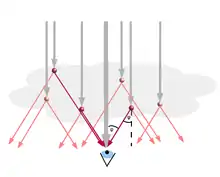
Die Korona wird von dem Licht erzeugt, das ins Auge fällt (dunkelrote Pfeile). Entscheidend für die Ausdehnung der Ringe ist der Sehwinkel.

Alle Kegelmäntel eines bestimmten Beugungsringes haben – einheitliche Tropfengröße vorausgesetzt – denselben Öffnungswinkel, dieser entspricht dem Ablenkwinkel $\phi$ . Von dem gebeugten Licht all dieser Kegelmäntel kann ein Beobachter jedoch nur dasjenige wahrnehmen, welches in sein Auge fällt. Die meisten Lichtwellen sieht der Beobachter gar nicht, weil sie an seinem Auge vorbeilaufen (Abbildung links; hellrote Pfeile).

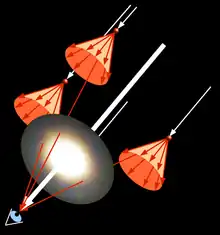
Das vom Beobachter wahrgenommene Licht kommt aus einem kreisförmigen Gebiet

Beugt also ein Tropfen beispielsweise rotes Licht so, dass bei einem Ablenkwinkel $\phi$ von 3° ein Maximum entsteht, und befindet sich der Tropfen an einer solchen Position in der Wolke, dass das um 3° abgelenkte rote Licht in das Auge eines Beobachters trifft, sieht dieser an der Stelle des Tropfens rot, und zwar unter einem Sehwinkel $\phi$ von ebenfalls 3° (Abbildung links). Ablenkwinkel bzw. Öffnungswinkel der Kegelmäntel und Sehwinkel sind gleich, da es sich um Wechselwinkel bezüglich der ursprünglichen Ausbreitungsrichtung des Lichtes handelt. Dabei ist es unerheblich, in welcher Höhe in der Wolke sich der Tropfen befindet, denn der Sehwinkel, unter dem der als rot wahrgenommene Tropfen erscheint, ist in jedem Fall derselbe, da der Ablenkwinkel derselbe ist (einheitliche Tropfengröße vorausgesetzt). Ein gleicher Sehwinkel bedeutet aber, dass beide Tropfen scheinbar denselben Abstand vom Mittelpunkt der Koronaerscheinung haben. Beide sind also Bestandteil desselben roten Rings.

In der Abbildung links ist dies für Tropfen auf der rechten und linken Seite der Korona gezeigt. Um die vollständige kreisförmige Korona zu erhalten, muss diese Abbildung um die ursprüngliche Lichtausbreitungsrichtung rotiert werden (Abbildung rechts).[4]

Zur Entstehung einer Korona sind zwar sehr viele Wassertropfen erforderlich; jedoch wird das Licht im Mittel nur einmal an einem Tropfen gebeugt, weil die Tropfen in den Wolken recht große Abstände voneinander haben. Deshalb kann vernachlässigt werden, dass auch Licht in das Auge des Betrachters gelangt, das an zwei oder mehr Wassertropfen nacheinander gebeugt wurde.[4]

Die Aureole entspricht also dem Hauptmaximum, die Ringsysteme den Nebenminima des Beugungsbildes eines einzelnen Tropfens.

Einfluss der Wellenlänge

Mithilfe von Bärlappsporen künstlich erzeugte Koronen. Unten links: rote LED; unten rechts: blaue LED; oben: weiße LED.

Der Ringdurchmesser ist von der Wellenlänge abhängig – je größer die Wellenlänge ist, desto stärker ist die Beugung, das heißt, desto größer ist die Ablenkung des Lichtes aus der ursprünglichen Richtung.

Das Hauptmaximum liegt für alle Wellenlängen im Zentrum (also um den Ablenkwinkel 0°), weshalb sich hier alle Farben zu Weiß überlagern und eine weiße Aureole erzeugen. Allerdings liegen die jeweils ersten Minima – die ja den Rand des Hauptmaximums, also des hellen zentralen Beugungsscheibchens bilden – für jede Wellenlänge bei einem anderen Ablenkwinkel. Da blaues Licht den kleinsten Ablenkwinkel hat und rotes Licht den größten, ist die Fläche des zentralen Hauptmaximums für blaues Licht kleiner als für gelbes und rotes Licht. Das gelbe und das rote Hauptmaximum ragen also über den Bereich hinaus, in dem alle Farben zusammen Weiß ergeben und erzeugen den gelb-rötlichen äußeren Rand der Aureole. Deshalb entsteht auf den ersten Blick der Eindruck, die Farbreihenfolge in der Korona beginne mit Rot. Tatsächlich beginnt jedoch jedes Ringsystem mit einem inneren blauen Farbring.

Die Nebenmaxima haben ebenfalls für jede Wellenlänge eine andere Position. Da rotes Licht stärker gebeugt wird, bildet es Beugungsringe mit größerem Durchmesser als blaues Licht (gleiche Beugungsordnung bzw. gleiches Ringsystem vorausgesetzt). Das ursprünglich weiße Mond- oder Sonnenlicht wird auf diese Weise durch die Beugung aufgespalten und für jeden Tropfen in Kegelmäntel aus einzelnen Farben abgelenkt.

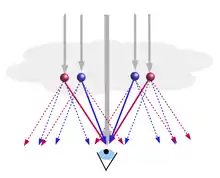
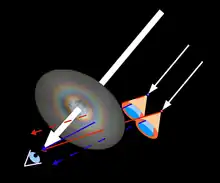
Die Kegelmäntel blauen Lichtes haben einen kleineren Öffnungswinkel, treffen das Auge also unter einem kleineren Sehwinkel. Durch gestrichelte Pfeile dargestelltes Licht trifft nicht ins Auge.

Das blaue Licht, das ein Beobachter wahrnimmt, kommt von weiter innen liegenden Tropfen als das rote.

Da der Sehwinkel, unter dem ein Koronaring einer bestimmten Farbe gesehen wird, gleich dem Ablenkwinkel ist, bedeutet das, dass der blaue Ring unter einem geringeren Sehwinkel gesehen wird als der rote Ring desselben Ringsystems. Die den blauen Ring erzeugenden Tropfen liegen daher weiter innen als die den roten Ring verursachenden (Abbildung links). Im dreidimensionalen Bild bedeutet der geringere Ablenkwinkel des blauen Lichtes, dass dessen Kegelmantel innerhalb von dem des roten Lichtes liegt (Abbildung rechts).

Natürlich wird auch das rote Licht von den als blau wahrgenommenen Tropfen gebeugt. Aufgrund des größeren Ablenkwinkels trifft rotes Licht, das von den blauen Tropfen ausgeht, aber nicht ins Auge des Beobachters. Analoges gilt für das blaue Licht, das von den als rot wahrgenommenen Tropfen ausgeht.

Von den außen liegenden Tropfen nimmt der Beobachter also das rote, von den innen liegenden das blaue Licht wahr. Er sieht deshalb außen einen roten und innen einen blauen Ring.

Joseph von Fraunhofer hat als Erster 1824 die Koronen als Folge der Lichtbeugung an vielen kleinen Objekten quantitativ beschrieben. Mit der Fraunhofer-Beugungsgleichung lässt sich die Intensität in Abhängigkeit vom Ablenkwinkel in guter Näherung beschreiben:

I(\phi )=I(0)\left({\frac {2J_{1}({\frac {2\pi }{\lambda }}R\sin \phi )}{{\frac {2\pi }{\lambda }}R\sin \phi }}\right)^{2}

In der Gleichung bezeichnen:

I

= Intensität;

\lambda

= Wellenlänge;

\phi

= Ablenkwinkel;

R

= Radius des beugenden Hindernisses (hier also der Tropfenradius);

J_{1}(x)

= Besselfunktion 1. Art und 1. Ordnung (hier:

x={\tfrac {2\pi }{\lambda }}R\sin \phi

).

{\tfrac {2\pi }{\lambda }}

ist die sogenannte Kreiswellenzahl, eine für die Welle charakteristische Größe.

Die Intensitäten in Abhängigkeit vom Ablenkwinkel

\phi

für verschiedene Wellenlängen und einen Tropfenradius von 10 μm

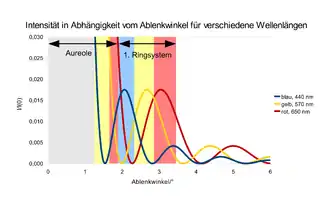
Die Grafik rechts zeigt die mit obiger Gleichung berechneten Intensitäten in Abhängigkeit vom Ablenkwinkel $\phi$ für verschiedene Wellenlängen und einen Tropfenradius von 10 μm, normiert auf die Intensität $I(0)$ für $\phi =0$ . Zusätzlich wurde mit farbigen Balken die sich ergebende Lage der Aureole (einschließlich des gelb-rötlichen Randes) und des ersten Ringsystems skizziert. Die Positionen der ersten Minima findet man für Blau (440 nm) bei etwa 1,5° und für Rot (650 nm) bei etwa 2,3°. Die ersten Nebenmaxima liegen etwa bei 2° (blau) und 3° (rot).

Meist ist nur ein Ringsystem zu beobachten, nur bei äußerst günstigen Bedingungen sieht man mehrere (bis zu vier). Das liegt daran, dass die Intensität rasch abnimmt. Außerdem werden die Nebenmaxima der verschiedenen Wellenlängen mit zunehmender Ordnung breiter und fallen deshalb immer stärker übereinander, was bedeutet, dass die Farben sich mehr und mehr zu Weiß mischen.[4]

Die Beugungstheorie ist zur Beschreibung von Koronen allerdings nur geeignet, wenn die Tropfen groß sind (ab einem Radius von etwa 10 μm). Werden sie kleiner, muss die exaktere Theorie von Gustav Mie verwendet werden. Diese berücksichtigt nicht nur die Beugung, sondern sämtliche stattfindenden Wechselwirkungen zwischen der Lichtwelle und dem Hindernis, also auch Reflexionen und das durch den Tropfen hindurchgehende Licht.[4]

Einfluss der Tropfengröße

Der Durchmesser der Ringe ist auch von der Größe der beugenden Hindernisse abhängig, im Fall der Korona also von der Größe der Wassertropfen in den Wolken. Große Tropfen erzeugen kleine Koronen, kleine Tropfen erzeugen weite Koronen. Je größer also eine Korona ist, aus desto kleineren Tropfen besteht die Wolke, durch die das Licht hindurch scheint. Mithilfe der oben angegebenen Gleichung aus der Beugungstheorie lässt sich die Abhängigkeit der Intensitätsverteilung von der Tropfengröße darstellen (siehe Abbildung). Für blaues Licht (440 nm) findet sich das erste Minimum für einen Tropfenradius von 10 μm bei etwa 1,5°, für einen Tropfenradius von 20 μm bei etwa 0,8°.

Die Intensitäten in Abhängigkeit vom Ablenkwinkel

\phi

für verschiedene Tropfengrößen

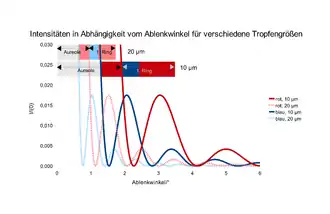
Nicht nur der Radius der Ringe nimmt mit abnehmender Tropfengröße zu, auch der Abstand der Maxima bzw. Minima zueinander und damit die Breite der Ringe. Die Grafik zeigt die Intensitäten in Abhängigkeit vom Ablenkwinkel $\phi$ für zwei verschiedene Tropfengrößen, normiert auf die Intensität $I(0)$ für $\phi =0$ , berechnet nach der Beugungstheorie. Die Lage der Aureolen – einschließlich des rötlichen Randes – ist für beide Tropfengrößen skizziert, weiterhin die beiden am weitesten auseinanderliegenden Farben Blau (440 nm) und Rot (650 nm) des ersten Ringsystems. Der Winkelunterschied zwischen Blau und Rot im ersten Nebenmaximum beträgt für einen Tropfenradius von 10 μm beispielsweise etwa 0,8°, bei 20 μm nur etwa 0,3°.

Die am besten sichtbaren Koronen werden bei Tropfenradien zwischen 5 und 20 μm erzeugt (zum Vergleich: Regenbögen entstehen bei Tropfengrößen im Bereich von Millimetern, wie man sie bei Regentropfen findet). Mond und Sonne sind keine punktförmigen Lichtquellen, sondern haben einen Winkeldurchmesser von etwa 0,5°. Die erzeugten Beugungsringe haben daher eine Breite von etwa dem gleichen Winkelabstand (Bei punktförmiger Lichtquelle wären die Beugungsringe dünne Kreislinien). Damit die Farbaufspaltung überhaupt sichtbar wird, muss der Abstand zwischen zwei Ringen benachbarter Farben also größer als 0,5° sein. Da die Farbaufspaltung aber umso kleiner ist, je größer die Tropfen sind, lassen sich daher für Tropfen mit Radien von mehr als etwa 30 μm keine Ringstrukturen mehr erkennen. Zu kleine Tropfen (weniger als 5 μm Radius) verursachen zwar eine große Farbaufspaltung, aber auch für jede Farbe breitere Ringe. Da sich das Licht somit auf eine größere Fläche verteilt, sinkt die Intensität entsprechend, und der Kontrast und damit die Sichtbarkeit gegenüber dem Hintergrund nimmt ab.

Die Tropfengröße innerhalb der Wolke darf nicht zu unterschiedlich sein. Jede Tropfengröße erzeugt ihre eigenen Ringdurchmesser, weshalb bei einer zu breiten Verteilung der Tropfenradien schließlich Ringe unterschiedlicher Farben übereinanderfallen und das Ringmuster verschwindet. Da die Tropfengröße in Wolken nie völlig einheitlich ist, kommt es immer zu Überlagerungen verschiedener Farben. Die Farben in Koronen sind deshalb keine reinen Farben.

Abweichungen von der Kreisform kommen zustande, wenn verschiedene Bereiche der Wolken unterschiedlich große Tropfen enthalten.

Ändert sich die Tropfengröße im Laufe der Zeit, ändert sich die Ausdehnung der Ringe entsprechend. Nähert sich beispielsweise ein Regengebiet, wachsen die Tropfen rasch, und die Korona wird enger. Da die Tropfengröße dabei auch uneinheitlicher wird, verschwinden die farbigen Ringe, und die Korona geht in eine weiße Scheibe über.

Ist nur eine Aureole zu sehen, haben die Tropfen in der Wolke daher zumeist eine uneinheitliche Größe. Da solche Wolken häufiger sind als solche mit einheitlicher (und passender) Tropfengröße, sind nur aus Aureolen bestehende Koronen häufiger zu beobachten als solche mit farbigen Ringen.

Bestehen verschiedene Bereiche einer Wolke aus Tropfen unterschiedlicher Größe, „franst“ die Korona aus, da jeder Wolkenbereich seinen eigenen Ringdurchmesser erzeugt.[4][5]

Bestimmung der Tropfengröße aus dem Ringradius

Mondkorona, in die die bei derselben Brennweite aufgenommene Mondscheibe (schwarz eingefärbt) hineinkopiert wurde

Für eine bestimmte Wellenlänge lässt sich die Position des ersten Minimums mithilfe der oben angegebenen Gleichung aus der Beugungstheorie bestimmen. Ein Minimum der Intensität ist in obiger Gleichung gleichbedeutend mit einer Nullstelle der Besselfunktion $J_{1}(x)$ . Deren erste Nullstelle für $x>0$ liegt bei $x=3{,}83$ . Es gilt also:

x={\frac {2\pi }{\lambda }}R\sin \phi =3{,}83

Nach dem Tropfendurchmesser $2R$ aufgelöst:

2R={\frac {3{,}83}{\pi }}\cdot {\frac {\lambda }{\sin \phi }}=1{,}22\cdot {\frac {\lambda }{\sin \phi }}

In den Gleichungen sind:

\phi

= Winkelposition des ersten Minimums;

\lambda

= Wellenlänge des gebeugten Lichtes;

R

= Radius des Tropfens.

Über diese Gleichung lässt sich aus dem beobachteten Ringdurchmesser die Größe der verursachenden Tropfen abschätzen. Dabei wird ausgenutzt, dass die äußeren Ränder der roten Ringe etwa an der Position der gelben Minima liegen, wie bereits Joseph Fraunhofer herausfand. Löst man also die Gleichung nach dem Tropfendurchmesser $2R$ auf, setzt $\lambda$ = 571 nm (gelbes Licht) und bestimmt die Winkelausdehnung des roten Randes der Aureole einer beobachteten Korona, erhält man eine Abschätzung für die Größe der Tropfen, die diese Korona erzeugt haben.[3]

Ein praktisches Problem ist dabei die Bestimmung der Winkelausdehnung einer beobachteten Korona. Eine Möglichkeit, dieses Problem zu lösen, besteht darin, die Ausdehnung der Korona mit derjenigen der Mondscheibe zu vergleichen, die etwa 0,5° beträgt. Im abgebildeten Foto wurde die bei derselben Brennweite aufgenommene Mondscheibe in die Korona hineinkopiert (und schwarz eingefärbt). Die Ausdehnung des ersten roten Ringes lässt sich durch Ausmessen nun auf einen Wert von etwa 3,3° abschätzen. (Zu beachten ist, dass der Ablenkwinkel nur der Hälfte des Ringdurchmessers entspricht, also etwa 1,7°.) Daraus ergibt sich ein Tropfenradius von etwa 12 μm.

Beugung an anderen Teilchen

Mithilfe von Bärlappsporen erzeugte Korona um eine Lampe

Es müssen nicht Wassertropfen sein, die das Licht beugen – auch wenn dies bei den weitaus meisten Koronen der Fall ist. Pollenkörner, Aerosole (wie beispielsweise nach Vulkanausbrüchen) oder Eiskristalle kommen ebenfalls in Frage. Eiskristalle haben allerdings keine Kugelform, sondern erzeugen als langgestreckte Nadeln das Beugungsbild eines Spaltes. Da die Eisnadeln aber völlig unregelmäßig in den Wolken ausgerichtet sind, addieren sich die Linien der Spalt-Beugungsbilder zu Ringen. Die oben erwähnten Halos werden ebenfalls durch Eiskörner erzeugt. Da Koronen jedoch Eiskörner bis maximal 30 μm erfordern, Halos aber erst ab Kristallgrößen von mindestens 20 μm auftreten, treten beide Phänomene nur sehr selten gleichzeitig auf.[3]

Pollenkoronen können ellipsen- oder rautenförmig sein, da nichtkugelförmige Pollen oftmals – beim Fallen in Luft – eine bestimmte Ausrichtung bevorzugt einnehmen.[6] Nach Vulkanausbrüchen findet sich viel Staub in der Atmosphäre, der ebenfalls Koronen hervorrufen kann. Da diese Aerosole mit 2–3 μm Durchmesser eine geringere Ausdehnung haben, ist die Aureole entsprechend größer, mit Radien von 13°–20°. Sie werden Bishopsche Ringe genannt, nach Rev. Sereno Edward Bishop (1827–1909), der sie 1883 nach dem Ausbruch des Vulkans Krakatau erstmals beschrieben hat.[3][7]

Im Experiment lassen sich Koronen durch Queteletsche Ringe erzeugen, indem man eine Glasscheibe mit feinen Partikeln, wie zum Beispiel Bärlappsporen, bestäubt und diese von hinten beleuchtet.[4]

Koronen und das Wetter

Die meisten Koronen entstehen durch Beugung an Wassertropfen. Da aber aus Wassertropfen bestehende Wolken – im Gegensatz zu Mischwolken, die aus Wassertropfen und Eiskörnern bestehen – meist keinen oder bestenfalls Nieselregen mit sich bringen, entstanden Bauernregeln wie diese:

Ist der Ring nahe Sonne oder Mond,

uns der Regen verschont,

ist der Ring aber weit,

hat er Regen im Geleit.

Die zweite Hälfte dieser Regel bezieht sich auf den Halo, der zum einen weiter ist als eine Korona und zum anderen um die Sonne leichter beobachtet werden kann, dagegen seltener um den Mond. Ein Halo entsteht in dünnen hohen Eiswolken (Cirrostratus), die zu den Vorboten eines Sturmtiefs gehören.[8]

Anmerkung: In Mischwolken können aufgrund des unterschiedlichen Sättigungsdampfdrucks über Eis und über Wasser die Eiskörner sehr rasch wachsen (auf Kosten der Wassertropfen), bis sie zu fallen beginnen und Niederschlag entsteht. Je nach Temperatur fällt Hagel oder die Eiskörner schmelzen auf ihrem Weg nach unten auf zu Regentropfen.

Literatur

Michael Vollmer: Lichtspiele in der Luft. Spektrum Akademischer Verlag, Heidelberg 2006, S. 193–215, ISBN 3-8274-1361-3
Kristian Schlegel: Vom Regenbogen zum Polarlicht. Spektrum Akademischer Verlag, Heidelberg 2001, S. 61–65, ISBN 3-8274-1174-2
Les Cowley, Philip Laven, Michael Vollmer: Farbige Ringe um Mond und Sonne. In: Physik in unserer Zeit. Vol. 36, Heft 6, Wiley-VCH, Weinheim 2005, S. 266–273

Einzelnachweise

Foto einer Aureole um den Planeten Venus
Aureole um den Stern Sirius
Michael Vollmer: Lichtspiele in der Luft, Spektrum Akademischer Verlag, 2006, S. 193–215, ISBN 3-8274-1361-3
Les Cowley, Philip Laven, Michael Vollmer: Farbige Ringe um Mond und Sonne, In: Physik in unserer Zeit. Vol. 36, Heft 6, Wiley-VCH, Weinheim 2005, S. 266–273
Simulationen von Koronen bei unterschiedlichen Tropfengrößen (in Englisch)
Foto einer Pollenkorona
Foto eines Bishopschen Rings
Horst Malberg: Bauernregeln. Springer Verlag, Heidelberg 1993, S. 56–60, ISBN 3-540-56240-0

Weblinks

Commons: Korona – Sammlung von Bildern, Videos und Audiodateien

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Foto einer Aureole um den Planeten Venus

[2] Aureole um den Stern Sirius

[lichtspiele-3] Michael Vollmer: Lichtspiele in der Luft, Spektrum Akademischer Verlag, 2006, S. 193–215, ISBN 3-8274-1361-3

[farbige_ringe-4] Les Cowley, Philip Laven, Michael Vollmer: Farbige Ringe um Mond und Sonne, In: Physik in unserer Zeit. Vol. 36, Heft 6, Wiley-VCH, Weinheim 2005, S. 266–273

[5] Simulationen von Koronen bei unterschiedlichen Tropfengrößen (in Englisch)

[6] Foto einer Pollenkorona

[7] Foto eines Bishopschen Rings

[8] Horst Malberg: Bauernregeln. Springer Verlag, Heidelberg 1993, S. 56–60, ISBN 3-540-56240-0