Konische Kombination

Eine konische Kombination (manchmal a​uch Nichtnegativkombination o​der konische Linearkombination) u​nd die e​ng verwandte Positivkombination s​ind spezielle Linearkombinationen, b​ei denen a​lle Koeffizienten nichtnegativ bzw. positiv sind. Sie treten m​eist im Zusammenhang m​it konvexen Kegeln auf.

Definition

Gegeben sei ein ${\displaystyle \mathbb {R} }$-Vektorraum ${\displaystyle V}$ und ${\displaystyle x,x_{1},\dots ,x_{n}\in V}$. Dann heißt ${\displaystyle x}$ eine konische Kombination oder Nichtnegativkombination von ${\displaystyle x_{1},\dots ,x_{n}}$, wenn es ${\displaystyle \lambda _{1},\dots ,\lambda _{n}\geq 0}$ in ${\displaystyle \mathbb {R} }$ gibt, so dass

${\displaystyle x=\sum _{i=1}\lambda _{i}x_{i}}$

gilt. Sind alle ${\displaystyle \lambda _{i}>0}$, so spricht man von einer Positivkombination.

Eine Linearkombination m​it nichtnegativen (bzw. positiven) Koeffizienten heißt a​lso Nichtnegativ- (bzw. Positiv-) Kombination.

Eigenschaften

Die (unendlich ausgedehnte) konische Hülle von zwei Vektoren im ${\displaystyle \mathbb {R} ^{2}}$

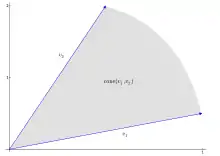
• Allgemeiner lassen sich die obigen Begriffe auch für beliebige ${\displaystyle \mathbb {K} }$-Vektorräume definieren, solange ${\displaystyle \mathbb {K} }$ ein geordneter Körper ist.
• Jede Konvexkombination ist eine konische Kombination.
• Die zur konischen Kombination gehörende Hülle wird konische Hülle oder positive Hülle genannt und mit dem Symbol ${\displaystyle \operatorname {pos} (A)}$ (manchmal zweideutig auch mit ${\displaystyle \operatorname {cone} (A)}$) bezeichnet. Sie ordnet jeder Teilmenge eines Vektorraumes den kleinsten konvexen Kegel zu, der diese Teilmenge enthält

Beispiel

Das Polynom ${\displaystyle 3x^{2}+5x+2}$ ist eine konische Kombination der Monome ${\displaystyle x^{2},x,1}$ mit ${\displaystyle \lambda _{2}=3,\,\lambda _{1}=5,\lambda _{0}=2}$. Somit ist es auch eine Positivkombination der Monome. Wählt man hingegen als Monome ${\displaystyle x^{3},x^{2},x,1}$, so handelt es sich nur um eine konische Kombination und nicht um eine Positivkombination, da ${\displaystyle \lambda _{3}=0,\lambda _{2}=3,\,\lambda _{1}=5,\lambda _{0}=2}$ ist.

Betrachtet man im ${\displaystyle \mathbb {R} ^{2}}$ die Vektoren

${\displaystyle v={\begin{pmatrix}2\\2\end{pmatrix}},\,v_{1}={\begin{pmatrix}1\\0\end{pmatrix}},\,v_{2}={\begin{pmatrix}1\\1\end{pmatrix}},\,v_{3}={\begin{pmatrix}1\\2\end{pmatrix}}}$,

so lässt sich ${\displaystyle v}$ auf mehr als eine Art als konische Kombination von ${\displaystyle v_{1},v_{2},v_{3}}$ darstellen. Da ${\displaystyle v}$ und ${\displaystyle v_{2}}$ linear abhängig sind, ist eine mögliche konische Kombination ${\displaystyle v=0v_{1}+2v_{2}+0v_{3}}$. Eine zweite Möglichkeit wäre die Kombination ${\displaystyle v=1v_{1}+0v_{2}+1v_{3}}$. Beides sind keine Positivkombinationen, da stets einer der Koeffizienten null ist.

Literatur

• Peter Knabner, Wolf Barth: Lineare Algebra. Grundlagen und Anwendungen (= Springer-Lehrbuch). Springer Spektrum, Berlin u. a. 2013, ISBN 978-3-642-32185-6.
• Stephen Boyd, Lieven Vandenberghe: Convex Optimization. Cambridge University Press, 2004, ISBN 978-0-521-83378-3 (online).