Isochronismus
Isochronismus (von griech.: isochron, gleich lange dauernd; andere Bezeichnungen: Isochronie, Tautochronie) bezeichnet die Eigenschaft eines mechanischen Schwingsystems, für eine Schwingung unabhängig von der Schwingungsweite (Amplitude) immer die gleiche Zeit zu benötigen.[1] Der Begriff ist für die Technik mechanischer Uhren zentral. Wenn bei Uhren keine konstante Schwingungsweite des Schwingsystems gewährleistet werden kann, führen Abweichungen vom Isochronismus zu Gangfehlern.
Der Terminus wird oft missverständlich benutzt. Im Gegensatz zu obiger Definition wird ein Schwingsystem als isochron bezeichnet, wenn es bei konstanter Schwingungsweite eine konstante Schwingungsdauer aufweist. Die Schwingung selbst ist zwar unter dieser Bedingung isochron (also gleich lang). Das System jedoch ist in der Regel kein isochrones, denn bei einer anderen Amplitude ergibt sich ggf. eine andere Schwingungsdauer. Man kann das als bedingten oder eingeschränkten Isochronismus bezeichnen.
Ferner gilt die Galilei zugeschriebene Aussage, ein Schwerependel-Schwingsystem sei ein isochrones, nur für kleine Ausschläge (siehe unten).
Ein mechanisches Schwingsystem besteht aus einem Körper (Masse), den eine rücktreibende Kraft (Reversierkraft, Gegenmoment) bei Auslenkung aus einer Mittellage (Nullstellung) wieder in diese Mittellage zurückzuführen sucht. In der mechanischen Uhrentechnik werden nur Körper verwendet, die um eine Drehachse ausgelenkt werden können:
- das Schwerependel (Galilei)
- die Unruh (Huygens[2])
- das Torsionspendel (von untergeordneter Bedeutung).
Rücktreibende Kräfte sind:[3]
- die Erdanziehung (Gravitation) beim Schwerependel
- Federkräfte
- Spiralfeder bei der Unruh
- Torsionsfeder beim Torsionspendel.
Theoretisch schwingt ein Schwingsystem isochron, wenn die rücktreibende Kraft linear (proportional) mit dem Auslenkwinkel ansteigt. Das ist weder beim Schwerependel noch bei der Unruh der Fall, wohingegen das Torsionspendel diese Eigenschaft besitzt. In der Praxis hat sich jedoch gezeigt, dass das Torsionspendel aus hier nicht zu erörternden Gründen dem Schwerependel und dem Unruh-Spirale-Schwingsystem unterlegen und für Präzisionsuhren nicht geeignet ist.
Der Isochronismusfehler des Schwerependels[4] ist dadurch bedingt, dass die rücktreibende Kraft mathematisch vom Sinus des Auslenkwinkels bestimmt wird (also nicht linear ist). Das Unruh-Spirale-Schwingsystem könnte sich prinzipiell isochron verhalten, wenn die Spiralfeder eine exakt lineare Rückstellkraft liefern würde. Das ist jedoch nur für kleine Amplitudenbereiche realisierbar, so dass auch dieses System nicht als isochron bezeichnet werden kann.
In mechanischen Uhren werden somit nichtisochrone Schwingsysteme verwendet (abgesehen vom Torsionspendel und vom unten beschriebenen Pendel mit kleiner Schwingungsweite).
Die Bestrebungen der Uhrmacher waren und sind deshalb einerseits darauf gerichtet, das Schwingsystem mit konstanter Amplitude schwingen zu lassen und andererseits die Größe der Rückstellkraft (der Unruhspirale bzw. der Torsionsfeder) in Abhängigkeit von der Auslenkung stabil zu halten (bedingter Isochronismus). Viele Einflüsse stehen dem entgegen (Einfluss der Hemmung auf das Schwingsystem, Temperaturschwankungen, Reibungsprobleme, Stöße durch Bewegung der Uhr, schwankendes Antriebsdrehmoment, Materialermüdung bei Federn usw.). Der Bau präziser mechanischer Uhren setzt voraus, dass alle diese Einflüsse durch geeignete Maßnahmen minimiert werden (Freie Hemmung, Kompensationspendel bzw. -unruh, Steinlagerung, optimierte Werkstoffe, konstantes Antriebsdrehmoment usw.).
Das Schwerependel weist insofern eine Besonderheit auf, als im Bereich sehr kleiner Amplituden die Schwingung als isochron anzusehen ist, weil dann mathematisch der Sinus des Auslenkwinkels durch den Auslenkwinkel ersetzt werden kann (Kleinwinkelnäherung)[5] und die Rückstellkraft somit mit großer Genauigkeit linear vom Auslenkwinkel abhängt. Beispielsweise ändert sich die Schwingungsdauer eines Pendels mit einer mittleren Amplitude von 2° bei Amplitudenschwankungen um ±1° nicht merkbar. Präzise Pendeluhren werden deshalb mit kleinen Auslenkwinkeln betrieben, wobei dennoch auch eine möglichst konstante Amplitude angestrebt wird. Erst mit der Erfindung der Grahamhemmung konnten Pendeluhren mit kleinen Pendelausschlägen gebaut werden.
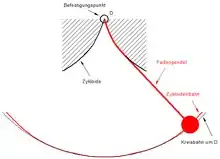
Auf Huygens geht die Erkenntnis zurück, dass sich ein Schwerependel theoretisch isochron verhält, wenn es statt auf einer Kreisbahn auf einer Zykloidenbahn schwingt. Um dies zu realisieren, erfand er die tautochrone Pendelaufhängung (Zykloidenpendel). Dabei ist das Pendel an einem dünnen Faden oder einer dünnen Blattfeder aufgehängt, wobei sich diese während der Schwingung an zykloidenförmige Backen anlegen. Dadurch wird das Pendel auf eine Zykloidenbahn gezwungen. Dieser Weg, die Schwingungsdauer des Schwerependels unabhängig von der Auslenkung zu machen, hat sich insbesondere aufgrund der damit verbundenen Reibungsprobleme nicht bewährt.
In der Uhrenliteratur sind die unpräzisen Begriffe „Isochronismus der Spirale“, „Isochrone Spirale“ o. Ä. zu finden. Eine Spirale ist jedoch ohne Unruh als Gangregler nicht verwendbar und kann deshalb auch nicht als isochron bezeichnet werden (bzw. der Spirale ein Isochronismus zugeschrieben werden). Meist sind Spiralen gemeint, die durch eine besondere Formgebung (Endkurven / Breguet, Phillips,[6] Gerstenberger) eine angenähert lineare Rückstellkraft (konstantes Direktionsmoment) für das Schwingsystem im Arbeitsbereich liefern. Aber auch Spiralen, deren Gestaltung (Anordnung der Befestigungspunkte) eine gegenseitige Kompensation von gegensätzlich wirkenden Störeinflüssen ermöglicht (Caspari, Grossmann), werden mit diesem Attribut versehen. Die Störursachen können dabei sowohl von der Spirale selbst als auch von anderen Bauteilen der Uhr herrühren.
Einzelnachweise
- Rudi Koch: BI-Lexikon Uhren und Zeitmessung, VEB Bibliographisches Institut Leipzig.
- Fritz von Osterhausen: Callweys Uhrenlexikon. Callwey, München 1999, ISBN 978-3766713537.
- Martinek Rehor: Mechanische Uhren. VEB Verlag Technik Berlin.
- Meschede: Gerthsen Physik. Springer.
- Recknagel: Physik Mechanik. VEB Verlag Technik Berlin.
- Edouard Phillips: Mémoire sur le spiral réglant des chronomètres et des montres. 1860, abgerufen am 1. April 2017 (französisch).