Inklusionsabbildung

Eine Inklusionsabbildung (kurz Inklusion), natürliche Einbettung o​der kanonische Einbettung i​st eine mathematische Funktion, d​ie eine Teilmenge i​n ihre Grundmenge einbettet.

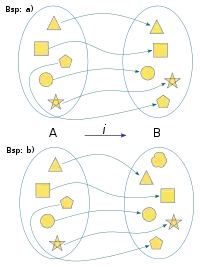
Zwei Beispiele für eine Inklusion. Bsp b) zeigt eine echte Inklusion.

Definition

Für Mengen ${\displaystyle A}$ und ${\displaystyle B}$ mit ${\displaystyle A\subseteq B}$ ist die Inklusionsabbildung ${\displaystyle i\colon A\rightarrow B}$ durch die Abbildungsvorschrift

${\displaystyle i(x)=x}$

gegeben. Manchmal wird das spezielle Pfeilsymbol ${\displaystyle \hookrightarrow }$ zur Kennzeichnung benutzt und man schreibt dann ${\displaystyle i\colon A\hookrightarrow B}$.

Man spricht von einer echten Inklusion, falls ${\displaystyle A}$ eine echte Teilmenge von ${\displaystyle B}$ ist, das heißt, wenn es Elemente in ${\displaystyle B\setminus A}$ gibt.

Im Fall mathematischer Strukturen i​st die s​o definierte Abbildung e​iner Unterstruktur strukturtreu, d. h. e​in Monomorphismus.

Eigenschaften

• Jede Inklusionsabbildung ist injektiv. Eine echte Inklusion ist nicht surjektiv.
• Ist ${\displaystyle A=B}$, so ist die Inklusion die Identitätsabbildung.
• Eine beliebige Funktion ${\displaystyle f\colon A\to B}$ lässt sich bezüglich der Verkettung von Funktionen zerlegen als ${\displaystyle f=h\circ g}$, wobei ${\displaystyle g}$ surjektiv und ${\displaystyle h}$ injektiv ist: Sei ${\displaystyle C=\operatorname {im} f\subseteq B}$ die Bildmenge von ${\displaystyle f}$ und ${\displaystyle g\colon A\to C}$ die Funktion, die auf ${\displaystyle A}$ mit ${\displaystyle f}$ übereinstimmt, also ${\displaystyle g(x)=f(x)}$. Für ${\displaystyle h\colon C\to B}$ nimmt man die Inklusionsabbildung.
• Ist ${\displaystyle f\colon A\to B}$ eine beliebige Funktion und ${\displaystyle X}$ eine Teilmenge der Definitionsmenge ${\displaystyle A}$, dann versteht man unter der Einschränkung ${\displaystyle f|_{X}}$ von ${\displaystyle f}$ auf ${\displaystyle X}$ diejenige Funktion ${\displaystyle g\colon X\to B}$, die auf ${\displaystyle X}$ mit ${\displaystyle f}$ übereinstimmt. Mit Hilfe der Inklusion ${\displaystyle i\colon X\to A}$ lässt sich die Einschränkung kurz schreiben als

${\displaystyle f|_{X}=f\circ i}$.

• Umgekehrt lässt sich jede Inklusionsabbildung ${\displaystyle i\colon A\hookrightarrow B}$ als Einschränkung einer geeigneten identischen Abbildung auffassen: ${\displaystyle i=\left(\operatorname {id} _{B}\right)|_{A}}$

Weblinks

• Eric W. Weisstein: Inclusion Map. In: MathWorld (englisch).
• Koro: Inclusion mapping. In: PlanetMath. (englisch)