Informationsbezirk
Informationsbezirk (auch Informationsmenge) ist ein Begriff aus der Spieltheorie, der dazu dient, imperfekte Information (auch unvollkommene Information) formal durch mathematische Objekte zu modellieren.
Beispiele
Beispiele für Spiele mit imperfekter Information sind die meisten Kartenspiele, bei denen ein einzelner Spieler in der Regel keine umfassende Information über die aktuell erreichte Spielsituation besitzt, weil jeder Spieler nur seine eigenen Karten kennt. Ein Informationsbezirk umfasst dann jeweils diejenigen Spielsituationen, die aus Sicht des Spielers, der aktuell eine Entscheidung zu treffen hat, nicht unterscheidbar sind. Charakterisiert wird dieser Informationsbezirk durch den bisherigen Spielverlauf, zu dem insbesondere der eigene Vorrat an Karten gehört.
Versteckt etwa ein Spieler I in einer Hand eine Münze und lässt Spieler II raten, in welcher sie sich befindet, so bilden die beiden möglichen Lagen der Münze für Spieler II einen Informationsbezirk.
Formaler Ansatz
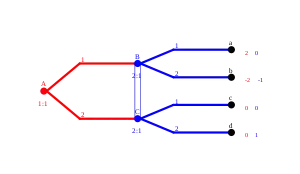
In Bezug auf das formale Modell eines extensiven Spiels ist ein Informationsbezirk eine Menge von Entscheidungsknoten, in denen sich ein Spieler in einer bestimmten Phase eines Spieles befinden kann, ohne aus dem bisherigen Spielverlauf sicher bestimmen zu können, in welchem Knoten er sich befindet.
In der graphischen Darstellung eines extensiven Spiels in Form eines Graphen wird ein Informationsbezirk gewöhnlich durch eine gestrichelte Linie durch alle Knoten des Bezirkes oder durch eine Kartusche dargestellt, die die Knoten des Informationsbezirkes einschließt.
Der Begriff des Informationsbezirks (information set) geht auf Harold W. Kuhn zurück, der ihn 1950 einführte.
Literatur
- H. W. Kuhn, Extensive games, PNAS, Band 36 (1950), S. 570–576.
- H. W. Kuhn, Extensive games and the problem of information, in: H. W. Kuhn, A. W. Tucker (Hrsg.), Contributions to the theory of games, vol. II, Princeton 1953, S. 193–216, doi:10.1515/9781400881970-012, (S. 193 in der Google-Buchsuche). Nachdruck in: H. Kuhn (Hrsg.), Classics in game theory, Princeton 1997, S. 46–68 (S. 46 in der Google-Buchsuche).
- Jörg Bewersdorff: Glück, Logik und Bluff: Mathematik im Spiel – Methoden, Ergebnisse und Grenzen, Wiesbaden 1998; 6. Auflage 2012, ISBN 978-3-8348-1923-9, doi:10.1007/978-3-8348-2319-9, S. 289 ff.