Indivisibilien
Die Indivisibilien (von lateinisch indivisibilia, „unteilbare [Größen]“), auch: Indivisibeln, ist eine frühneuzeitliche Bezeichnung für nicht teilbare kleinste Bestandteile von geometrischen Größen. Bonaventura Cavalieri benutzte indivisible Schnittflächen in geometrischen Körpern, um sein Volumenprinzip zu formulieren. Da die Theorie der Indivisibilien Unstimmigkeiten aufwies, wurden seit John Wallis und Gottfried Wilhelm Leibniz stattdessen infinitesimale Größen benutzt.
Geschichte
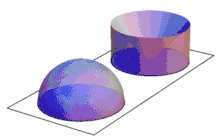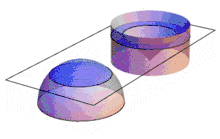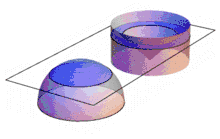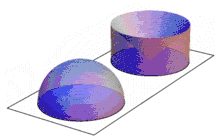
Der Mathematiker Bonaventura Cavalieri untersuchte Paare von geometrischen Körpern, deren sämtliche waagerechten Schnittflächen in jeweils derselben Höhe den gleichen Flächeninhalt besitzen. Dabei verwendet er ein widersprüchliches Konzept, das sich für die Geometrie aber als sehr nützlich erwies: Das Prinzip von Cavalieri besagt, dass Körper mit gleichgroßen Schnitten dasselbe Volumen haben. Die genannten Schnittflächen sind horizontal als unteilbar dünn konzipiert und heißen deshalb Indivisibilien. Dieser heute nur noch historisch benutzte Ausdruck entstammt einer Übersetzung des Ausdrucks ta átomia (altgriechisch τὰ ἄτομία) aus der Kritik von Aristoteles an der Atomlehre des Demokrit ins Lateinische.[1]
Cavalieri entwickelte eine Methode, aus diesen unteilbaren Schnittflächen Körper zusammenzusetzen. Obwohl Cavalieri die Auffassung, das geometrische Kontinuum sei aus Indivisibilien zusammengesetzt (ebenso wie Aristoteles) verwirft, sei eben diese Auffassung gleichwohl mit der Methode verträglich, die zum Cavalieriprinzip führt.[2] Laut Wolfgang Breidert hat diese Indifferenz zwischen Cavalieris Indivisibilienmethode und der aristotelischen Naturphilosophie zu einer Emanzipation der Mathematik gegenüber der Philosophie geführt.[3]
Horizontal unteilbare Schnittflächen lassen sich genau genommen nicht zu ausgedehnten Schnittscheiben zusammenfügen: Die Addition von Größen ohne jede Ausdehnung kann keine Größe mit Ausdehnung ergeben. Cavalieri verfügte noch nicht über die mathematischen Verfahren, das unendlich Kleine widerspruchsfrei und beweisbar darzustellen.
Seit dem siebzehnten Jahrhundert ersetzten John Wallis (Infinitesimal), Gottfried Wilhelm Leibniz (Differential) und andere die Indivisibilien durch infinitesimale Größen und im neunzehnten Jahrhundert verliehen Augustin Louis Cauchy, Karl Weierstraß, Richard Dedekind und andere der Analysis durch den Grenzwertbegriff eine mathematisch genaue Form.
Literatur
- Kristi Andersen: Cavalieri's method of indivisibles. Archive for History of Exact Sciences 31, S. 291–367 1985.
- Wolfgang Breidert: Das aristotelische Kontinuum in der Scholastik. Aschendorff Verlag, Münster 1970, 2. Aufl. 1979 (BGPhThMA, N. F. Bd. 1).
- Bonaventura Cavalieri: Geometria indivisibilibus., 1635
- Gottfried Leibniz, Sir Isaac Newton: Über die Analysis des Unendlichen – Abhandlung über die Quadratur der Kurven. Ostwalds Klassiker der exakten Wissenschaften, Band 162, Verlag Harri Deutsch, ISBN 3-8171-3162-3
- Christian Thiel: Indivisibilien. In: Jürgen Mittelstraß (Hrsg.): Enzyklopädie Philosophie und Wissenschaftstheorie. Zweite Auflage. Band 3, Metzler, Stuttgart/Weimar 2008, S. 593–594.
Einzelnachweise
- Metaphysik (Aristoteles): VII (Z) 1039a10 Bei Zeno.org 121
- Christian Thiel: Indivisibilien. S. 593
- Wolfgang Breidert: Das aristotelische Kontinuum in der Scholastik. 1970