I&Q-Verfahren

Das I&Q-Verfahren (In-Phase-&-Quadrature-Verfahren) ist eine Möglichkeit, bei einer Demodulation eines hochfrequenten Trägersignals die Phaseninformation zu erhalten. Damit kann man z. B. beim Radar bewegte von nicht bewegten Objekten unterscheiden. Es wird ebenfalls außerhalb der Hochfrequenztechnik z. B. zur Bestimmung von Winkellagen verwendet.

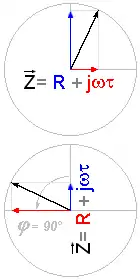
Bei einer einfachen Demodulation wird nur der Realteil eines komplexen Signals ermittelt, also von einem Signal, welches am Eingang des Demodulators eine Amplitudengröße und eine Phasenlage hat, liegt am Ausgang der Demodulatorschaltung nur noch die Amplitudengröße an, die Phaseninformation ist verlorengegangen.

Die Auswertung der Phaseninformation ist aber die Voraussetzung für eine MTI-Schaltung, die in dem Signal eine Doppler-Verschiebung der Trägerfrequenz erkennt und somit bewegte Objekte von unbewegten unterscheiden kann.

Bei der einfachen Demodulation kann es sogar vorkommen, dass der Momentanwert (Realteil) der Amplitude gleich Null ist und die Phaseninformation (Imaginärteil) ihren Maximalwert hat. Am Ausgang der einfachen Demodulatorschaltung wird in diesem Fall also kein Signal messbar sein. Das hat fatale Auswirkungen bei Radargeräten, die nach dem Monopulsverfahren arbeiten, die also zur Zielerkennung nur diesen einen Impuls benötigen. Es muss also das ganze Signal um 90° phasenverschoben werden, um in diesem Fall überhaupt ein demoduliertes Signal zu erhalten.

Da aber nicht bekannt ist, mit welcher Phase das Signal empfangen wird, müssen beide Wege der Demodulation durchgeführt werden:

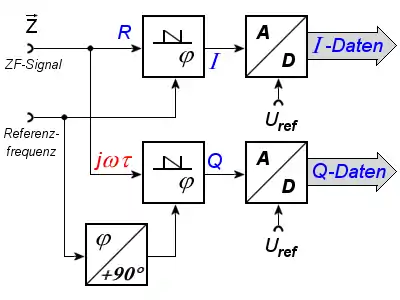
Das Signal wird also in zwei Wege aufgeteilt, der eine Weg der Demodulation wird mit der originalen Phasenlage (englisch: in phase) durchgeführt und ergibt die I-Daten, der zweite Weg wird mit um 90° phasenverschobener Referenzfrequenz durchgeführt und ergibt die Q-Daten (englisch: quadrature). Die Größe der Einzelkomponenten I und Q können mit einer Winkelfunktion berechnet werden:

{\begin{aligned}I&=A\cos {\Phi }\\Q&=A\sin {\Phi }\end{aligned}}

Daraus kann eine Rückrechnung des Phasenwinkels Φ vorgenommen werden:

\Phi =\arctan {\frac {Q}{I}}

Bei einer direkten Berechnung des Phasenwinkels in dieser Art sollte man den Phasenwinkel mit der arctan2() Funktion bestimmen um Probleme mit einer Division durch Null für I = 0, zu vermeiden und um alle vier Quadranten unterscheiden zu können.

Das I-Signal ist am Ausgang dieser Schaltung eine Amplitude, die den Realteil des momentan anliegenden Signals beschreibt. Das Q-Signal ist ebenfalls eine Amplitude, die aber den zugehörigen Imaginärteil repräsentiert. Aus beiden Amplituden kann nun, da sie im Ursprung in einem rechten Winkel zueinander stehen, mit dem Satz des Pythagoras die absolute Größe des empfangenen Echosignals errechnet werden.

A^{2}=I^{2}+Q^{2}

oder

A={\sqrt {I^{2}+Q^{2}}}

Näherungsrechnungen

In der Praxis ist allerdings die technische Realisierung einer Wurzelberechnung kompliziert. Zusätzlich sollen in diesem Stadium der Signalverarbeitung die Radardaten möglichst noch in Echtzeit vorliegen. Verzögerungen (interne Laufzeiten durch Rechenschritte) sollten immer gleich groß sein, um sie später kompensieren zu können. Deshalb wird hier meist mit einem Näherungsverfahren weitergearbeitet.

c\approx a+{\frac {b}{2}}

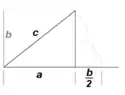
Die Länge der längeren Kathete a plus die halbe Länge der kürzeren Kathete b ist ungefähr die Länge der Hypotenuse c. Diese Formel lässt sich dagegen sehr leicht mit einem Assembler-Programm oder sogar mit einer extrem schnellen Hardware-Verdrahtung (zum Beispiel in einem FPGA) realisieren. Die Näherung ist größer oder gleich dem wahren Wert, mit einem maximalen Fehler von 12 % bei 26°.[1]

Neben der Näherung des Pythagoras ist auch eine wesentlich exaktere Berechnung mit Hilfe des CORDIC-Algorithmus möglich, der häufig in der digitalen Signalverarbeitung und im Mobilfunk Anwendung findet und ebenfalls für Echtzeitanwendungen in Frage kommt. Der CORDIC bietet eine ressourcenschonende Implementierung zur iterativen Drehung von Zeigern, bildet also die trigonometrischen Funktionen über einfachere Funktionen ab. Bei konkreter Verwendung des CORDIC im Bereich der I&Q-Demodulation wird der Zeiger des Eingangssignals auf Deckung mit dem Einheitszeiger gedreht (CORDIC-Vektormodus), woraus sich die Länge (Amplitude) und der Phasenwinkel ergeben.

Andere Anwendungen

Das I&Q-Verfahren wird nicht nur in der Hochfrequenz verwendet, sondern zum Beispiel auch bei Drehwinkelgebern. Liefert ein solcher Geber zwei um 90° versetzte Signale wird er daher auch als Quadratur-Encoder oder -Sensor bezeichnet. Die phasenverschobenen Signale können dabei sowohl analog als auch wertdiskret (digital) sein.

Siehe auch

Quadraturamplitudenmodulation

Einzelnachweise

siehe grafische Darstellung

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] siehe grafische Darstellung