Hufeisenlemma

Das Hufeisenlemma gehört z​u den Grundlagen d​er homologischen Algebra. Es besagt, d​ass die d​rei Moduln i​n einer kurzen exakten Sequenz s​o aufgelöst werden können (projektiv o​der injektiv), d​ass eine k​urze exakte Folge v​on Auflösungen entsteht.

Das Ergebnis k​ommt – allerdings o​hne Namen – bereits 1956 i​m Buch v​on Cartan u​nd Eilenberg vor.[1]

Das Lemma

Sei ${\displaystyle 0\rightarrow L\,{\xrightarrow {f}}\,M\,{\xrightarrow {g}}N\rightarrow 0}$ eine kurze exakte Folge von Moduln, oder allgemeiner von Objekten in einer abelschen Kategorie ${\displaystyle {\mathcal {A}}}$. Seien ${\displaystyle P_{*}^{L}\,{\xrightarrow {\varepsilon ^{L}}}\,L}$ und ${\displaystyle P_{*}^{N}\,{\xrightarrow {\varepsilon ^{N}}}\,N}$ projektive Auflösungen. Dann gibt es eine projektive Auflösung ${\displaystyle P_{*}^{M}\,{\xrightarrow {\varepsilon ^{M}}}\,M}$ und Kettenhomomorphismen ${\displaystyle P_{*}^{L}\,{\xrightarrow {f_{*}}}\,P_{*}^{M}\,{\xrightarrow {g_{*}}}\,P_{*}^{N}}$ derart, dass

1. ${\displaystyle 0\rightarrow P_{*}^{L}\,{\xrightarrow {f_{*}}}\,P_{*}^{M}\,{\xrightarrow {g_{*}}}\,P_{*}^{N}\rightarrow 0}$ ist eine kurze exakte Folge von Kettenkomplexen. Das heißt, in jedem Grad ist ${\displaystyle 0\rightarrow P_{n}^{L}\,{\xrightarrow {f_{n}}}\,P_{n}^{M}\,{\xrightarrow {g_{n}}}\,P_{n}^{N}\rightarrow 0}$ eine – aufgrund der Projektivität von ${\displaystyle P_{n}^{N}}$ notwendigerweise zerfallende – kurze exakte Sequenz.
2. Das resultierende Diagram
   
   

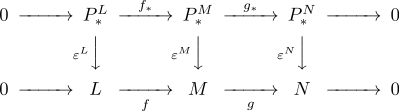   Das resultierende Diagramm
   
   kommutiert. Das heißt, es ist ${\displaystyle f\circ \varepsilon ^{L}=\varepsilon ^{M}\circ f_{0}}$ und ${\displaystyle g\circ \varepsilon ^{M}=\varepsilon ^{N}\circ g_{0}}$.

Die entsprechende Aussage für injektive Auflösungen g​ilt auch.

Zum Namen

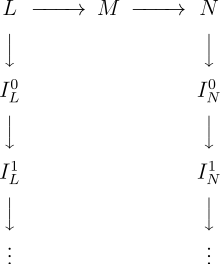
Das „Hufeisen“ (injektiver Fall)

Die Input-Daten ähneln e​inem Hufeisen, d​as Lemma füllt d​as Hufeisen aus.

Anwendungen

• Es gibt zwei Wege, den Begriff abgeleiteter Funktor zu definieren. Der Beweis, dass diese beide Wege äquivalent sind, benutzt das Hufeisenlemma und das Schlangenlemma. Die beiden Wege:
  1. Konstruktion über eine projektive bzw. injektive Auflösung.
  2. Charakterisierung als ein universeller δ-Funktor.
• Das Hufeisenlemma erlaubt auch die Konstruktion von Cartan–Eilenberg-Auflösungen.

Literatur

• Joseph J. Rotman: An introduction to homological algebra. 2. Auflage. Springer Verlag, New York 2009, ISBN 978-0-387-24527-0, S. 349–350.
• Charles A. Weibel: An introduction to homological algebra (= Cambridge studies in advanced mathematics. Nr. 38). Cambridge University Press, 1994, ISBN 0-521-43500-5, S. 37.

Einzelnachweise

1. Henri Cartan, Samuel Eilenberg: Homological Algebra (= Princeton Mathematical Series. Nr. 19). Princeton University Press, 1956, LCCN 53-010148, S. 80, Proposition V.2.2.