Gossensches Gesetz

Als Gossensche Gesetze bezeichnet man zwei volkswirtschaftliche Regeln, die auf der Annahme basieren, dass individuelle Präferenzen in Form von Nutzen quantifizierbar sind. Demnach kann dem Grad der Bedürfnisbefriedigung eines Individuums ein Wert zugewiesen werden, der in Nutzeneinheiten berechnet und ggfs. mit verschiedenen Nutzeneinheiten verrechnet werden kann.

Die Regeln sind von dem deutschen Volkswirt Hermann Heinrich Gossen (1810–1858) 1854 in seinem Werk Entwickelung der Gesetze des menschlichen Verkehrs und der daraus fließenden Regeln für menschliches Handeln aufgestellt worden, waren lange unbeachtet und wurden erst später als Gossensche Gesetze oder Gesetzmäßigkeiten der Bedürfnisbefriedigung bezeichnet.

Entdeckt wurde das Werk nach dem Tod Gossens von einem Kollegen von Stanley Jevons, der sich zu dieser Zeit noch mit Leon Walras darum stritt, wem die Urheberschaft der wesentlichen Überlegungen der subjektiven Wertlehre zufallen sollte – Jevons Arbeit datiert auf 1871, Walras' 1874. Nachdem sie von Gossens Werk erfuhren, erkannten aber beide dessen Priorität an.[1]

Erstes Gossensches Gesetz

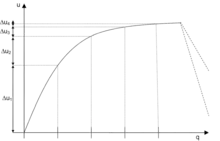
Abnehmen des Grenznutzens (u = Nutzen, Δu = Grenznutzen, q = konsumierte Menge)

Das erste Gossensche Gesetz (auch Gesetz vom abnehmenden Grenznutzen oder Sättigungsgesetz) lautet: „Die Größe eines und desselben Genusses nimmt, wenn wir mit Bereitung des Genusses ununterbrochen fortfahren, fortwährend ab, bis zuletzt Sättigung eintritt.“[2] Das Gesetz besagt also, dass der Konsum eines Gutes mit zunehmender Menge einen immer geringeren Zusatznutzen (Grenznutzen) stiftet.

Das erste Gossensche Gesetz greift damit unter der Annahme kardinal messbaren Nutzens die für die meisten Aktivitäten als gültig erachtete Hypothese auf, dass die erste Aktivitätseinheit mehr (zusätzlichen) Nutzen stiftet als die zweite, die zweite mehr als die dritte, die dritte mehr als die vierte und so weiter. Repräsentiert man Präferenzen über den Konsum nur eines Gutes durch eine differenzierbare Nutzenfunktion, so besagt das erste Gossensche Gesetz, dass die zweite Ableitung der Nutzenfunktion negativ ist.

Paradebeispiel ist der Konsum von Nahrungsmitteln, bei denen typischerweise Sättigung eintritt (und in der Folge der Grenznutzen auch negativ werden kann). So stiftet der Genuss eines ersten Glases Wasser durch einen Durstigen einen sehr hohen Nutzen, wohingegen das zweite bereits einen etwas geringeren, das dritte wiederum etwas weniger zusätzlichen Nutzen bringt und das vierte vielleicht schon Völlegefühl oder Übelkeit verursacht, d. h. der Grenznutzen schlägt ins Negative um. Der Extremfall könnte soweit gehen, dass man im Wasser ertrinkt, falls zu viel davon da ist.

Mathematische Formulierung des 1. Gossenschen Gesetzes (Abnehmender Grenznutzen) im 2-Güter-Fall:

{\begin{aligned}{\frac {\partial u(x_{1},x_{2})}{\partial x_{1}}}>0,{\frac {\partial u(x_{1},x_{2})}{\partial x_{2}}}>0\\{\frac {\partial ^{2}u(x_{1},x_{2})}{\partial x_{1}^{2}}}<0,{\frac {\partial ^{2}u(x_{1},x_{2})}{\partial x_{2}^{2}}}<0\end{aligned}}

Bedeutung

Das Gesetz erscheint als empirische Regelmäßigkeit unmittelbar plausibel, ist aber in weiten Bereichen der mikroökonomischen Theorie verzichtbar. Es ist weitgehend durch die Annahme ersetzt, dass die Bessermengen einer Präferenzrelation konvex sind (anschaulich: abnehmende Grenzrate der Substitution zwischen je zwei Gütern). Eine Ausnahme bilden stochastische Modelle, in denen Wirtschaftssubjekte Entscheidungen treffen, deren Konsequenzen zufallsbehaftet sind. Hier ist die Annahme eines abnehmenden (zunehmenden) Grenznutzens einer zufallsbehafteten Auszahlung (bzw. die strenge Konkavität (Konvexität) der Nutzenfunktion) äquivalent zur Annahme risikoaversen (risikoaffinen) Verhaltens, da der Nutzen des Erwartungswertes der möglichen Auszahlungen bei einer solchen Nutzenfunktion größer (kleiner) ist als der Erwartungswert der jeweiligen Nutzen der möglichen Auszahlungen.

Beispiel:

Mögliche Auszahlungen:

0

und

100

Wahrscheinlichkeiten: Jeweils

0{,}5

Erwartungswert der Auszahlungen:

0{,}5\cdot 0+0{,}5\cdot 100=50

Bei abnehmendem Grenznutzen steigt der Nutzen $U$ unterproportional zur Auszahlung, z. B. $U(0)=0;U(50)=3;U(100)=4$ . Hier wäre dann der Nutzen des Erwartungswertes der Auszahlungen $U(50)=3$ größer als der Erwartungswert der Nutzen der Auszahlungen $\operatorname {E} (U(0);U(100))=\operatorname {E} (0;4)=0{,}5\cdot 0+0{,}5\cdot 4=2$ .

Man beachte die Ähnlichkeit zu Johann Heinrich von Thünens Gesetz des sinkenden Grenzertrags.

Zweites Gossensches Gesetz

Andere Bezeichnungen sind: Equimarginalprinzip, Grenznutzenausgleichsregel, Gesetz vom Ausgleich der gewogenen Grenznutzen, gossensches Grenznutzenausgleichsgesetz und Genussausgleichsgesetz.

„„Der Mensch, dem die Wahl zwischen mehren [sic!] Genüssen frei steht, dessen Zeit aber nicht ausreicht, alle vollaus sich zu bereiten, muß, wie verschieden auch die absolute Größe der einzelnen Genüsse sein mag, um die Summe seines Genusses zum Größten zu bringen, bevor er auch nur den größten sich vollaus bereitet, sie alle teilweise bereiten, und zwar in einem solchen Verhältnis, daß die Größe eines jeden Genusses in dem Augenblick, in welchem seine Bereitung abgebrochen wird, bei allen noch die gleiche bleibt.“[3]“

– Hermann Heinrich Gossen (1854)

Beim zweiten Gossenschen Gesetz geht es um die Verteilung des Einkommens auf eine Vielzahl von Bedürfnissen, um einen höchsten Gesamtnutzen zu erzielen.

Ein Haushalt befindet sich demnach in einem Haushaltsoptimum, wenn seine Grenznutzen für alle Güter, jeweils geteilt durch den Preis des Gutes, übereinstimmen. Andernfalls könnte er seinen Nutzen steigern, da sich eine Umstrukturierung des Konsums so vornehmen ließe, dass eine Ausgabenreduzierung bei einem Gut weniger Nutzeneinbuße als eine entsprechende Ausgabenerhöhung bei einem anderen Gut Nutzenzuwachs bedeutet. Das zweite Gossensche Gesetz gilt sowohl für ordinale als auch für kardinale Nutzenmessung (wobei Gossen selbst von kardinaler Nutzenmessbarkeit ausging).

Die Aussage, dass im Haushaltsoptimum das Preisverhältnis je zweier Güter mit dem Verhältnis ihrer Grenzrate der Substitution (Steigung der Indifferenzkurve) übereinstimmen muss, ist zum zweiten Gossenschen Gesetz äquivalent.

Bezeichnet man die Konsumgütermengen der $n$ einem Individuum zur Verfügung stehenden Güter mit $x_{1},\ldots ,x_{n}$ , seine (differenzierbare) Nutzenfunktion mit $u=u(x_{1},\ldots ,x_{n})$ , und die Preise der Güter mit $p_{1},\ldots ,p_{n}$ , so lässt sich das zweite Gossensche Gesetz mathematisch wie folgt darstellen:

{\frac {\partial u(x_{1},\ldots ,x_{n})/\partial x_{1}}{p_{1}}}=\ldots ={\frac {\partial u(x_{1},\ldots ,x_{n})/\partial x_{n}}{p_{n}}}.

Geltungsbereich und Kritik

Gossens Werk, die Entwickelung der Gesetze des menschlichen Verkehrs und der daraus fließenden Regeln für menschliches Handeln, beschreibt den Konsum in einer Naturwirtschaft, in der das Individuum nur für sich produziert. Der Konsum wird dabei nach der subjektiven Wertschätzung der Güter geplant. Der Wert hat bei Gossen einen rein individuellen Charakter. In Gossens Gesellschaft spielen weder kollektive Arbeit und Arbeitsteilung, noch Warenproduktion für den Tausch eine Rolle. Insofern beschreibt Gossen eine psychologische Nutzen-Theorie des isolierten Individuums, statt den „Verkehr“ in der Waren produzierenden Gesellschaft seiner Zeit – in der industriellen Revolution.

Literatur

Hermann Heinrich Gossen: Entwickelung der Gesetze des menschlichen Verkehrs, und der daraus fließenden Regeln für menschliches Handeln. Braunschweig 1854

Weblinks

Volkswirtschaftslehre - Das 1. Gossensche Gesetz – gehostet bei vimeo
Gossensche Gesetze – Definition im Gabler Wirtschaftslexikon
gossensche Gesetze – Artikel bei der Bundeszentrale für politische Bildung

Einzelnachweise

Ulrich van Suntum: Die unsichtbare Hand. 3. Auflage. Springer, 2005, Seite 36
Hermann Heinrich Gossen: Entwickelung der Gesetze des menschlichen Verkehrs, und der daraus fließenden Regeln für menschliches Handeln. Braunschweig 1854, S. 4f.
Hermann Heinrich Gossen: Entwickelung der Gesetze des menschlichen Verkehrs, und der daraus fließenden Regeln für menschliches Handeln. Braunschweig 1854, S. 12

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Ulrich van Suntum: Die unsichtbare Hand. 3. Auflage. Springer, 2005, Seite 36

[2] Hermann Heinrich Gossen: Entwickelung der Gesetze des menschlichen Verkehrs, und der daraus fließenden Regeln für menschliches Handeln. Braunschweig 1854, S. 4f.

[3] Hermann Heinrich Gossen: Entwickelung der Gesetze des menschlichen Verkehrs, und der daraus fließenden Regeln für menschliches Handeln. Braunschweig 1854, S. 12