Globales Matching
Globales Matching bezeichnet im Rahmen der Informationsintegration einen Prozess zur automatischen Abbildung verschiedener Schemas aufeinander (Schema-Matching). Dabei werden Ergebnisse aus verschiedenen Matching-Verfahren verwendet, um Attribute der zu matchenden Schemas tatsächlich aufeinander abzubilden.
Begriffsklärung
Durch das Globale Matching wird versucht, die Attribute und Relationen verschiedener Schemas (im Allgemeinen zwei) miteinander in Beziehung zu setzen. Globales Matching kann daher auf zweierlei Arten verstanden werden.
- Globales Matching ist ein „normales“ Matching-Verfahren, das Attribute (ganze Spalten) miteinander matcht,
- Globales Matching ist andererseits ein Schritt, der aus den bereits gewonnenen Informationen tatsächliche Matches zwischen den Attributen (und Relationen) zweier Schemas generiert. Er versucht, möglichst die richtigen Matches auszuwählen, die zusammen ein möglichst gutes Mapping der beiden Schemas bilden.
Im Folgenden wird die zweite Interpretation behandelt. Da sich Globales Matching sowohl auf die Ergebnisse einfacher als auch auf Ergebnisse zusammengesetzter Matcher beziehen kann, lässt es sich nicht in die Kategorisierung des Schema Matchings einordnen.
Problemstellung
Die Matchings zwischen zwei beliebigen Attributen zweier unterschiedlicher Schemas werden durch vorhergehende Matchingverfahren (z. B. Edit-Distance, (künstliche) neurale Netze oder Similarity Flooding) mit einer Wahrscheinlichkeit belegt. Die Schwierigkeit besteht nun darin, diejenigen Paare aus Attributen auszuwählen, die tatsächlich zusammengehören. Es reicht dabei im Allgemeinen nicht aus, jedem Attribut des ersten Schemas das Attribut des zweiten Schemas mit der größten Korrespondenzwahrscheinlichkeit zuzuordnen. Es können die folgenden Probleme auftreten:
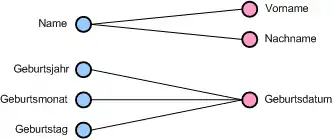
- Mehrere Attribute des zweiten Schemas haben hinsichtlich eines Attributes des ersten Schemas die gleiche Ähnlichkeit. Eventuell sind sie sogar „echt“ semantisch ähnlich wie das folgende Beispiel zeigt.
- Statt 1:1-Matches gibt es 1:n-Matches, beispielsweise wenn Vorname und Nachname in einem anderen Schema als Attribut „Name“ zusammengefasst sind. Es müssen also genau die richtigen Attribute (ggf. sogar in der richtigen Reihenfolge und mit dem richtigen Konkatenationsoperator) ausgewählt werden.
- Einige Attribute dürfen vielleicht nicht gematcht werden, weil sie im anderen Schema keine Entsprechung besitzen.
- Die schiere kombinatorische Komplexität der möglichen Paarungen lässt die Berechnung lange dauern. Zudem erschweren es die tatsächlich gefundenen und dem Benutzer vorgeschlagenen Paarungen dem Benutzer, das Ergebnis zu bewerten. Das gilt insbesondere dann, wenn sich viele false Positives darunter befinden.
Grenzen des Globalen Matchings
Globales Matching zielt darauf ab, zwei Schemas aufeinander abzubilden und sich dafür der Hilfe verschiedener Matching-Verfahren zu bedienen, die die Ähnlichkeiten zwischen den Attributen ausgerechnet/geschätzt haben.
Die derzeit auf dem Markt verfügbaren Lösungen bieten häufig nur 1:1-Mappings an und verlassen sich auf strukturelle oder Namensähnlichkeiten. Sie lösen also nicht alle der zuvor geschilderten Probleme.
Workflow
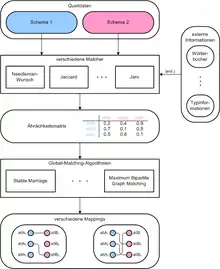
Im Folgenden wird der Workflow beim Global Matching gezeigt.
Gegeben sind zwei Schemas, die integriert werden sollen. In der Praxis könnte dabei das eine Schema das Quellschema sein, aus dem die Daten in ein Zielschema migriert werden sollen. Dies ist beispielsweise bei der Übernahme eines Unternehmens durch ein anderes Unternehmen denkbar. Das Schema des übernommenen Unternehmens wäre dabei das Quellschema, das andere entsprechend das Zielschema. Aus den entsprechenden Schemas werden die interessierenden Relationen und Attribute ausgewählt, beispielsweise ein Produktkatalog, während Kunden- oder Umsatzdaten ignoriert werden.
Im nächsten Schritt müssen die ausgewählten Attribute gematcht werden. Dazu wird eine bestimmte, nicht-leere Menge an Matchern ausgewählt, die die paarweise Ähnlichkeit der ausgewählten Attribute ermittelt. Die Matcher bedienen sich je nach Typ und Verfügbarkeit externer Daten wie beispielsweise Wörterbüchern oder den in der Datenbank abgelegten Typinformationen oder Fremdschlüsselbeziehungen.
Die Ergebnisse der Matcher werden in einer Ähnlichkeitsmatrix aufgestellt. Wurden mehrere Matcher benutzt, müssen die Einzelergebnisse gewichtet und gegebenenfalls normalisiert werden. Die Ähnlichkeitsmatrix gibt für jedes Attributpaar (gebildet aus je einem Attribut beider Schemas) an, wie gut/wahrscheinlich beide Paarteilnehmer semantisch zusammenpassen. Die Ähnlichkeitswerte müssen nicht notwendigerweise im Intervall [0, 1] liegen. Im Allgemeinen lässt sich die Ähnlichkeitsmatrix nicht durch Umsortieren der Zeilen oder Spalten in eine Einheitsmatrix umwandeln; Attributen aus dem einen Schema sind also meist mehrere Attribute mit einer gewissen Ähnlichkeit aus dem anderen Schema zugeordnet und umgekehrt. Durch Algorithmen wie dem Similarity Flooding kann die Ähnlichkeitsmatrix verbessert werden. Eine Ähnlichkeitsmatrix kann auch als Liste dargestellt werden, deren Einträge Tripel (Attribut1, Attribut2, Ähnlichkeitswert) sind.
Um die folgende Arbeit effizienter zu gestalten und die Anzahl der False Positives zu verringern, ist vor dem nächsten ein Zwischenschritt denkbar, der die Ähnlichkeitsmatrix filtert. Dabei können beispielsweise Schwellwerte für die Ähnlichkeiten festgelegt werden. Geringere Ähnlichkeiten werden als zu unwahrscheinlich angesehen und auf 0 gesetzt. Zudem können Typinformationen einbezogen werden, falls dies nicht durch die Matcher bereits erledigt wurde. Der Zwischenschritt mag implizit erfolgen, wenn die Zusammenfassung mehrerer Matchingverfahren durch einen kombinierenden Matcher erledigt wurde und er danach die Filterung intern vornimmt.
Aus der (nun möglicherweise ausgedünnten) Ähnlichkeitsmatrix werden anschließend Mappings gewonnen. Ein Mapping ist eine Auswahl eineindeutiger Zuordnungen zwischen Elementen beider Mengen, wobei es auch Elemente geben kann, die keinem Element der anderen Menge zugeordnet sind. Da im Allgemeinen immer noch keine bzw. nicht nur 1:1-Zuordnungen in der Ähnlichkeitsmatrix vorliegen, gibt es mehrere theoretisch denkbare Mappings. Die Ähnlichkeitsmatrix erzeugt also ein Multimapping,[1] aus dem mehrere Mappings erzeugt werden können. Es gibt verschiedene Algorithmen, „gute“ Mappings auszuwählen. Sie werden im nächsten Abschnitt vorgestellt. Die durch die Algorithmen erzeugten Mappings werden dem Benutzer anschließend präsentiert.
Algorithmen
Nachfolgend sollen einige Mapping-Algorithmen kurz erläutert werden. Sie versuchen jeweils, Paare aus Elementen zweier Mengen zu bilden, zu denen Metainformationen über die Wahrscheinlichkeit des Zusammenpassens (die Ähnlichkeitsmatrix) bekannt sind.
Stable Marriage
Der Stable-Marriage-Algorithmus von Gale und Shapely[2] versucht, zwei Elemente derart zusammenzubringen, dass sie mit ihrem der Wahrscheinlichkeit nach passendsten Pendant (also dem mit dem größten Wert) verbunden sind, das nicht selbst wiederum mit einem anderen Element mit noch höherer Wahrscheinlichkeit verbunden ist. Übertragen formuliert gibt es zwei Personengruppen, Männer und Frauen, wobei jede Person eine Rangliste von allen Personen des anderen Geschlechts besitzt. Die Personen werden nun so verheiratet, dass keine Person mit einer anderen verheiratet ist, die nicht die höchstmögliche Stellung in der Präferenzliste verbliebener Heiratskandidaten besetzt.
Elemente sind hierbei die kleinen Kreise, die jeweils zur Menge der gleichfarbigen Kreise gehören.
Dieser Algorithmus wird anhand des folgenden Beispiels erklärt.
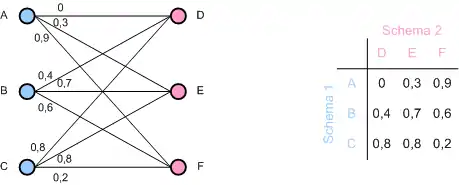
Der linke und der rechte Teil zeigen dieselbe Ähnlichkeitsmatrix.
Für den Algorithmus muss die Ähnlichkeitsmatrix in zwei Präferenzlisten umgewandelt werden, in eine „aus Sicht der blauen Menge“ und in eine „aus Sicht der roten Menge“. Dabei spielen die Zahlenverhältnisse keine Rolle, sondern nur die Reihenfolge. Die Reihenfolge entsteht durch ein Null-basiertes Abzählen der Elementindizes (A bzw. D haben beispielsweise den Index 0, C und F dagegen den Index 2). Die Präferenzlisten sehen folgendermaßen aus:
„Präferenzliste der blauen Menge“ „Präferenzliste der roten Menge“
A: 2 1 0 D: 2 1 0
B: 1 2 0 E: 2 1 0
C: 0 1 2 F: 0 1 2
unter Auflösung der Indizes:
„Präferenzliste der blauen Menge“ „Präferenzliste der roten Menge“
A: F E D D: C B A
B: E F D E: C B A
C: D E F F: A B C
Diese Umwandlung ist nicht eindeutig, die Präferenzliste von C hätte auch 1 0 2 lauten können. Eine konkrete Implementation muss sich für eine Variante entscheiden. Ein weiterer Indeterminismus bleibt bestehen, da „Frau D und Frau E in der gleichen Reihenfolge um die Männer konkurrieren“. Mit anderen Worten: Die Reihenfolge der Attribute ist für das Ergebnis relevant.
Nachdem die Präferenzlisten erstellt wurden, kann der eigentliche Algorithmus beginnen. Dabei werden die Attribute der einen Menge durchgegangen. Die jeweils „best-passendsten“ Attribute des anderen Schemas werden als Match vorgemerkt. Dabei kann der Fall auftreten, dass ein Attribut bereits vorgemerkt ist, bei einem anderen aber in der Präferenzliste an vorderster Stelle steht. Um diesen Konflikt zu lösen, wird in der Präferenzliste des strittigen Attributes nachgesehen, welches der beiden konkurrierenden Attribute die höhere Ähnlichkeit hat. Ist es das bereits vorgemerkte, ändert sich nichts und es wird versucht, das „unterlegene“ Attribut gegen das nächste in seiner Präferenzliste zu matchen. Besitzt das dritte Attribut jedoch bezüglich des zu matchenden Attributes eine höherwertige Stelle in der Präferenzliste, wird diese Paarung vorgemerkt und die alte vorgemerkte Paarung gestrichen.
Eigenschaften
Ein Stable-Marriage-Mapper erfordert eine gleiche Anzahl an Attributen im Quell- und Zielschema und mappt die beiden Schemas vollständig. Dabei erzeugt er 1:1-Mappings.
Er ist mehrdeutig beim Erstellen der Präferenzlisten und auch beim Abwickeln der Paarbildungen, bei der es auf die Reihenfolge ankommt. Er wählt für jedes Attribut das bestmögliche Mapping aus.
Maximum Weighted Bipartite Graph Matching
Die Ähnlichkeitsmatrix kann auch als Graph verstanden werden, der bipartit ist (zwei Knotenarten), ungerichtet und gewichtet. Dieser soll transformiert werden in einen Graphen, der zudem noch unzusammenhängend ist, in dem also gerade genau zwei Knoten miteinander verbunden sind. Dazu müssen lediglich „die richtigen“ Kanten des ersten Graphen ausgewählt und in den zweiten Graphen übernommen werden.
Der Maximum-Weighted-Bipartite-Graph-Matching-Algorithmus (z. B. umgesetzt durch den Ungarischen Algorithmus) versucht, die Summe der Gewichte der „aktivierten“ Kanten zu maximieren, was übertragen auf das Hochzeitsproblem einer Maximierung der Gesamtzufriedenheit entspricht, auch auf die Gefahr hin, Einzelpersonen untermaximal zufriedenzustellen.
Dafür müssen zunächst die Werte der Ähnlichkeitsmatrix in Distanzmaße umgewandelt werden, beispielsweise, indem man die jeweilige Ähnlichkeit von eins abzieht. Anschließend wird von jeder Zeile das Zeilenminimum abgezogen, dann von jeder Spalte das Spaltenminimum. Dadurch ergeben sich zwangsläufig Nullen. Diese Nullen werden durch einen oder mehrere gedachte Balken abgedeckt, jedoch mit so wenigen wie möglich. Stimmt die Zahl der Balken mit der Anzahl der Attribute überein, wird zeilenweise die darin enthaltene Null gesucht. Gibt es nur eine Null, definiert sie den Match der beiden Attribute. Zeile und Spalte werden gelöscht. Gibt es mehrere, wird sie zunächst ausgelassen und mit der nächsten Zeile fortgefahren. Anschließend wiederholt sich der Ablauf für Spalten.
Die Implementierung von Brian Milch[3] beruht auf dem Ungarischen Algorithmus von Harold Kuhn und benötigt lediglich die Ähnlichkeitsmatrix als Eingabe. Sie produziert folgendes Mapping:
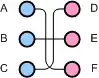
Eigenschaften
Der Maximum-Weighted-Bipartite-Graph-Matching-Algorithmus erlaubt das Mappen von Schemas unterschiedlicher Größe. Er erzwingt jedoch vollständige Mappings. Zudem wird die Summe der Gewichte der ausgewählten Kanten maximiert.
Royal Couples
Royal Couples wurde von Marie und Gal als Alternative zum Stable-Marriage-Algorithmus vorgestellt. Um die fortwährenden Änderungen der Liste der vorgemerkten Paare zu umgehen, werden einfach gleich die Attribute miteinander verbunden, die am besten zueinander passen, das „Royal Couple“. Dadurch kann es keine Paarung geben, die besser passt, die Vormerkung also nicht zerstört werden. Nachdem die beiden Paarteilnehmer einander zugeordnet wurden, gehen sie natürlich keine weitere Paarung mehr ein und können aus der Ähnlichkeitsmatrix gelöscht werden, samt der Zeile und Spalte, in der sie standen.
Nüchtern betrachtet ist dies jedoch genau der naive Ansatz, der die Paare sortiert nach der Ähnlichkeit auswählt und entfernt.
Eigenschaften
Royal Couples maximiert zwar nicht die Gesamtähnlichkeit des Mappings, erzeugt jedoch eine Stable Marriage. Außerdem werden sämtliche Attribute gemappt und es gibt lediglich 1:1-Matches.
Dominants Matching
Marie und Gal stellen im selben Paper einen weiteren Algorithmus vor, der ein Problem von Royal Couples und auch dem Maximum-Weighted-Bipartite-Graph-Matching-Algorithmus lindert. Bei diesen Algorithmen bewirkt die Auswahl eines Paares das Löschen einer Zeile und einer Spalte der Ähnlichkeitsmatrix, da ja gerade die beiden Attribute fortan nicht mehr gematcht werden können. Dadurch werden auch Ähnlichkeiten entfernt, die ebenfalls einen relativ hohen, aber nicht maximalen Wert haben. Dies eröffnet ein neues Problem sowie eine neue Perspektive. Das Problem hierbei ist, dass durch die fehlende Löschung der Zeilen und Spalten Attribute mehrmals gematcht werden können. Eine höhere Instanz muss das Filtern der Paare übernehmen. Betrachtet man jedoch das Mehrfachauftreten als gewollt, so erhält man m:n-Mappings.
Der Algorithmus läuft so ab, dass jeweils die Zeilen- und Spaltenmaxima markiert werden. Die Zellen der Ähnlichkeitsmatrix, die gleichzeitig Zeilen- und Spaltenmaximum sind, bilden die Korrespondenzen. Letztendlich ist dieser Algorithmus nur eine Aufweichung des Royal-Couples-Algorithmus, bei dem nicht die gesamte Zeile und Spalte einer gefundenen Korrespondenz gelöscht wird, sondern nur die jeweilige Zelle. Bezieht man dies jedoch auf Mehrfachmappings, bedeutet dies einen Fortschritt, der mit Royal Couples allein nicht möglich wäre.
Eigenschaften
Dominants Matching erlaubt das Mapping von Schemas unterschiedlicher Größe. Es erzwingt kein vollständiges Mapping, da Attribute, die zu allen Attributen des anderen Schemas nur eine geringe Ähnlichkeit aufweisen, nicht in das Mapping einbezogen werden. Sie besitzen entweder ein Zeilen- oder ein Spaltenmaximum, jedoch nicht beides. m:n-Mappings sind möglich.
Royal Groups
Der Royal-Groups-Algorithmus verfolgt zwei Ziele. Erstens wird die Präzision erhöht, da die Zahl falscher Korrespondenzen verringert wird, zweitens werden Cluster aus eventuell zusammengehörenden Attributen gebildet. Diese können entweder m:n-Mappings sein oder einfache Mappings. Die Clusterbildung wird insbesondere im zweiten Fall als eingeschränkte Umgebung für Korrespondenzalternativen angesehen. Der Benutzer kann die richtige Korrespondenz dann leichter auswählen.
Royal Groups basiert auf dem Royal-Couples-Algorithmus, führt aber einen Schwellwert für die Ähnlichkeit ein. Ähnlichkeiten unter diesem werden gedanklich auf 0 gesetzt und verhindern die entsprechende Paarung. Dadurch wird der Zwang, ein vollständiges Mapping zu erstellen, eliminiert. Der Vorteil daran ist, dass die Zahl der False Positives reduziert wird. Der Benutzer wird entlastet, weil er dadurch weniger offensichtlich falsche Korrespondenzen manuell löschen muss.
Außerdem werden geringe Unterschiede in den Ähnlichkeitswerten geglättet. Es erscheint unpassend, eine Ähnlichkeit von 0,99 einer Ähnlichkeit von 0,95 absolut vorzuziehen, wenn sich andere Ähnlichkeiten erkennbar niedriger bewegen. Daher wird eine zusätzliche Größe eingeführt, die der ε-Umgebung. Wird ein Ähnlichkeitsmaximum gefunden, werden alle die Werte in derselben Zeile und Spalte ebenfalls als Maximum aufgefasst, deren Ähnlichkeiten innerhalb der durch ε bestimmten Umgebung zum Maximum liegen. Dadurch können die oben beschriebenen Cluster gebildet werden, Cliquen genannt.
Die Schwierigkeit besteht bei Royal Groups jedoch darin, geeignete Parameter zu finden. Sie hängen vom verwendeten Matcher ab. Erzeugt er für falsche Korrespondenzen Werte nahe 0 und für richtige Korrespondenzen Werte nahe 1, könnte der Schwellwert bei 0,8 liegen und der ε-Wert bei 0,1. Ist das Maximum zum Beispiel 0,92, würden Attribute, die eine Ähnlichkeit von 0,86 besitzen, als gleichwertig bzw. gleich wahrscheinlich betrachtet und in die Clique aufgenommen.
Eigenschaften
Royal Groups erzwingt kein vollständiges Mapping und benötigt keine gleich großen Attributmengen. Es kann m:n-Mappings erzeugen.
Vergleich
Die genannten Eigenschaften der Algorithmen in einer tabellarischen Darstellung:
| Kriterium | Royal Couples | Stable Marriage | MWBG | Dominants Matching | Royal Groups |
|---|---|---|---|---|---|
| Zwang, vollständiges Mapping zu erzeugen | ja | ja | ja | nein | nein |
| Erlaubt m:n-Mappings | nein | nein | nein | noch nicht | ja |
| Charakteristik | Einfachheit | „zufriedenstes“ Attributmatching | Maximierung der Gesamtzufriedenheit | schneller, geringerer Recall | „toleranteres“ Ähnlichkeitsmaß |
| Bester Match sicher enthalten | ja | ja | nein | ja | ja |
| Komplexität |
Schlussbemerkungen
Kommerzielle Programme wie der Microsoft BizTalk-Mapper oder der IBM Rational Data Architect unterstützen keine m:n-Mappings. Die dort eingesetzten Algorithmen entsprechen von den Ergebnissen her den hier vorgestellten 1:1-Algorithmen. Durch die Einbeziehung eines Schwellwertes ließen sich die Ergebnisse filtern und somit die Precision erhöhen. Dem Benutzer bleibt natürlich dann die Frage überlassen, welchen Schwellwert er angeben soll. Der Dominants-Algorithmus befreit den Benutzer davon. Er „blendet“ falsche Korrespondenzen von selbst „aus“.
Der Royal-Groups-Algorithmus hingegen bietet an vielen dieser „ausgeblendeten“ Stellen eine kurze Liste von Vorschlägen an. Der Benutzer kann sie schnell durchgehen und überflüssige Korrespondenzen löschen. Als „Bonus“ werden dabei auch m:n-Mappings gefunden. Diese muss sich der Benutzer jedoch durch die Feinjustage des Schwellwertes und der Epsilon-Umgebung erkaufen, die vom verwendeten Matcher abhängen.
Einzelnachweise
- Melnik et al.: Similarity Flooding: A Versatile Graph Matching Algorithmand its Application to Schema Matching. Abgerufen am 13. August 2019.
- D. Gale und S. Shapely: “College Admissions and the Stability of Marriage.” The American Mathematical Monthly 69.1 (Jan., 1962): 9-15.
- BLOG Inference Engine (Memento vom 16. Juni 2011 im Internet Archive)