Gegenbauer-Polynom

Die Gegenbauer-Polynome, auch ultrasphärische Polynome genannt, sind eine Menge orthogonaler Polynome auf dem Intervall ${\displaystyle [-1,1]}$ mit der Gewichtungsfunktion ${\displaystyle (1-x^{2})^{\alpha -1/2}}$, mit ${\displaystyle \alpha >-1/2}$. Sie sind benannt nach dem Mathematiker Leopold Gegenbauer und bilden die Lösung der Gegenbauer-Differentialgleichung. Die Polynome haben die Form

${\displaystyle C_{n}^{(\alpha )}(z)={\frac {1}{\Gamma (\alpha )}}\sum _{m=0}^{\lfloor n/2\rfloor }(-1)^{m}{\frac {\Gamma (\alpha +n-m)}{m!(n-2m)!}}(2z)^{n-2m},}$

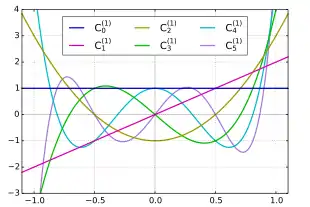
Gegenbauer-Polynome mit α=1

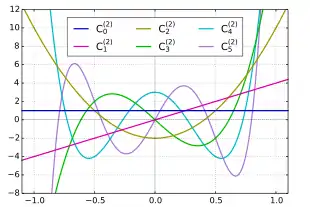
Gegenbauer-Polynome mit α=2

für ${\displaystyle \alpha \neq 0}$, andernfalls

${\displaystyle C_{n}^{(0)}(z)=\sum _{m=0}^{\lfloor n/2\rfloor }(-1)^{m}{\frac {(n-m-1)!}{m!(n-2m)!}}(2z)^{n-2m},}$

Sie lassen sich auch durch eine hypergeometrische Funktion ${\displaystyle {}_{2}F_{1}}$ darstellen:

${\displaystyle C_{n}^{(\alpha )}(z)={\frac {(2\alpha +n-1)!}{(2\alpha -1)!\,n!}}\,_{2}F_{1}\left(-n,2\alpha +n;\alpha +{\frac {1}{2}};{\frac {1-z}{2}}\right)}$

Der Wert für ${\displaystyle z=1}$ ist

${\displaystyle C_{n}^{(\alpha )}(1)={n+2\alpha -1 \choose n}.}$

Die ersten Polynome h​aben die Gestalt:

${\displaystyle C_{0}^{(\alpha )}(z)=1}$

${\displaystyle C_{1}^{(\alpha )}(z)=2\alpha z}$

${\displaystyle C_{2}^{(\alpha )}(z)=-\alpha +2\alpha (1+\alpha )z^{2}}$

${\displaystyle C_{3}^{(\alpha )}(z)=-2\alpha (1+\alpha )z+4/3\alpha (1+\alpha )(2+\alpha )z^{3}}$

Referenzen

• Eric W. Weisstein: Gegenbauer Polynomial. In: MathWorld (englisch).
• Milton Abramowitz, Irene Stegun: Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover. ISBN 0-486-61272-4, S. 774.