Flussüberquerungsrätsel
Flussüberquerungsrätsel sind eine Gattung von Denksportaufgaben, bei denen es darum geht, eine Gruppe definierter Mitglieder mit möglichst wenigen Überfahrten über einen Fluss zu bringen, wobei das Boot nicht gleichzeitig die gesamte Gruppe fassen kann und bestimmte Konstellationen von Gruppenmitgliedern an den Ufern verboten sind. Die älteste schriftliche Überlieferung dieses Aufgabentyps findet sich in den Propositiones ad acuendos iuvenes aus dem späten 9. Jahrhundert, die vier solcher Aufgaben enthält. Unter diesen befindet sich auch das bekannteste Problem dieses Aufgabentyps, das Problem von Wolf, Ziege und Kohlkopf, bei dem ein Mann die beiden Tiere und den Kohlkopf über den Fluss bringen soll, wobei er gleichzeitig nur eines der Tiere oder den Kohlkopf mitnehmen kann und verhindern muss, dass der Kohl oder die Ziege gefressen werden.
Beispiele
Wolf, Ziege und Kohlkopf
Das Problem von Wolf, Ziege und Kohlkopf ist das bekannteste Beispiel für ein Flussüberquerungsrätsel. Dabei möchte ein Mann zusammen mit einem Wolf, einer Ziege und einem Kohlkopf einen Fluss überqueren, doch das Boot kann außer ihm nur einen weiteren Passagier fassen. Er kann weder den Wolf mit der Ziege noch die Ziege mit dem Kohl unbeaufsichtigt an einem Ufer lassen. Aufgabe ist es, einen Plan zu entwickeln, der diese Bedingungen einhält und mit möglichst wenigen Überfahrten auskommt.
Zur Lösung sollte der Mann zunächst mit der Ziege den Fluss überqueren, sie am anderen Ufer lassen und alleine zurückkehren. Anschließend fährt er den Wolf zur anderen Seite, lässt diesen dort und kehrt mit der Ziege zurück. Diese lässt er am Ausgangsufer, setzt mit dem Kohlkopf über und kehrt allein zurück. Schließlich bringt er die Ziege ein zweites Mal ans Zielufer, womit das Problem gelöst ist. Eine alternative Lösung ergibt sich, wenn man Wolf und Kohl in der obigen Reihenfolge austauscht.
Das Rätsel ist in vielen Kulturen verbreitet, wobei die Passagiere den lokalen Gegebenheiten angepasst werden. So ist das Problem auch mit Fuchs, Huhn und Körnern überliefert. Auch in Afrika ist das Rätsel weit verbreitet, hier kommen beispielsweise Gepard, Huhn und Reis vor.[1] Im Aarne-Thompson-Uther-Index werden Erzählungen mit diesem Motiv unter ATU 1579 angeführt, aber auch in modernen Unterhaltungsmedien wird oft auf dieses Rätsel zurückgegriffen.[2]
Die eifersüchtigen Ehemänner
Ebenfalls aus den Propositiones bekannt ist das Problem der eifersüchtigen Ehemänner: Drei Ehepaare (in den Propositiones sind es Geschwisterpaare) wollen einen Fluss überqueren, aber das Boot fasst nur zwei Personen. Die Ehemänner sind eifersüchtig aufeinander, sodass keiner es zulässt, dass seine Frau zusammen mit einem anderen Mann an einem Ufer oder im Boot sitzt, wenn er nicht dabei ist.
Eine leichtere Variante dieses Rätsels ergibt sich, wenn man die Bedingung etwas abschwächt: Die Frauen dürfen offenbar nie in der Überzahl sein (außer es sind gar keine Männer bei ihnen), denn sonst ist eine von ihnen mit einem fremden Mann zusammen, ohne dass ihr eigener dabei ist. In dieser Fassung wird die Aufgabe mit einer Umformulierung der Rahmenhandlung zum Problem der Missionare und Kannibalen: Drei Missionare und drei Kannibalen wollen einen Fluss überqueren, das Boot bietet aber nur Platz für zwei Personen. Um nicht fürchten zu müssen aufgefressen zu werden, dürfen die Missionare niemals in Unterzahl gegenüber den Kannibalen sein.
Die Brücke
Eine Variation des Aufgabentyps findet sich in Saul X. Levmores und Elizabeth Early Cooks Problem der Brückenüberquerung: Vier Personen, bezeichnet mit A, B, C und D, wollen bei Nacht eine Brücke überqueren, sie haben aber nur eine Laterne dabei. Ohne die Laterne ist es in der Dunkelheit unmöglich, die Brücke zu überqueren, ihr Schein reicht aber nur so weit, dass nur jeweils zwei Personen gleichzeitig über die Brücke gehen können. A braucht für eine Überquerung 5, B 10, C 20 und D 25 Minuten. Da die Laterne nicht mehr lange brennt, müssen sie einen Weg finden, um möglichst schnell die Brücke zu überqueren.[3]
Hier übernimmt die Laterne die Rolle des Bootes, statt der Zahl der Überquerungen soll ihre Dauer minimiert werden. In der naiven Lösung bringt A nacheinander die drei anderen auf die andere Seite, wobei er selbst zweimal zum Ausgangspunkt zurückkehrt. Dies dauert 10 + 5 + 20 + 5 + 25 = 65 Minuten. Es gibt jedoch eine schnellere Lösung: A und B überqueren die Brücke, A kehrt mit der Laterne zurück. Anschließend gehen C und D als die beiden langsamsten gemeinsam hinüber, die Laterne bringt B zurück, bevor er zusammen mit A die Brücke ein weiteres Mal überquert. Dieser Plan benötigt nur 10 + 5 + 25 + 10 + 10 = 60 Minuten.
Weitere Beispiele
Neben diesen bekannten Beispielen gibt es noch viele weitere Flussüberquerungsrätsel. So wurde das Problem der eifersüchtigen Ehemänner auch für eine größere Anzahl von Paaren gestellt, wobei zusätzlich eine Insel in der Mitte des Flusses eingeführt wird. Eine systematische Untersuchung mit vollständiger Lösung für dieses Problem stammt von Ian Pressman und David Singmaster.[4]
Eine kleine Sammlung verschiedener Flussüberquerungsrätsel findet sich auch im Rätselbuch Amusements in Mathematics von Ernest Dudeney.[5]
Mathematische Untersuchung
Aus mathematischer Sicht fallen Flussüberquerungsrätsel in das Gebiet der kombinatorischen Optimierung: Aus einer größeren, aber endlichen Zahl an zulässigen Lösungen soll die beste ausgewählt werden. Ein einfaches Modell für Flussüberquerungsprobleme liefert die Graphentheorie:[6] Ein Zustand kann dadurch beschrieben werden, dass man angibt, an welchem Ufer sich die einzelnen Personen und das Boot befinden. Zunächst streicht man die Zustände, die den Bedingungen widersprechen, die restlichen nimmt man als Knoten eines Graphen. Zwei Knoten werden durch eine Kante verbunden, wenn es eine zulässige Überfahrt zwischen ihnen gibt. Es ergibt sich ein Graph, in dem der kürzeste Weg vom Ausgangszustand zum Endzustand gesucht wird.
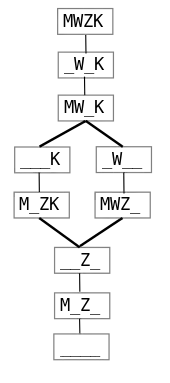
Im Beispiel von Wolf, Ziege und Kohlkopf kann man jeden Zustand beschreiben, indem man angibt, ob sich der Mann, der Wolf, die Ziege und der Kohl am Ausgangsufer befinden oder nicht. Da nur der Mann das Boot fahren kann, muss die Position des Bootes nicht extra angegeben werden. Es gibt also verschiedene Zustände, der Ausgangspunkt ist MWZK, das Ziel ____. Unter den 16 Zuständen sind 6 verboten: Bei _WZK, _WZ_ und __ZK ergibt sich am Ausgangsufer eine verbotene Konstellation, für die analogen Situationen am anderen Ufer müssen die Zustände M___, M__K und MW__ ausgeschlossen werden. Die restlichen 10 Zustände lassen sich leicht durch die erlaubten Überfahrten zu dem nebenstehenden Graphen verbinden, aus dem die beiden oben genannten Lösungen direkt abgelesen werden können.
Einzelnachweise
- Marcia Ascher: A River-Crossing Problem in Cross-Cultural Perspective. In: Mathematics Magazine. Vol. 63, Nr. 1, 1990. S. 26–29. (JSTOR 2691506)
-
- Piret Voolaid: Hundi, kitse ja kapsapea üle jõe viimine. ATU 1579 metamorfoosid. In: Mäetagused. Hüperajakiri Vol. 28, 2005. (online)
- Piret Voolaid: Carrying a Wolf, a Goat, and a Cabbage Across the Stream. Metamorphoses of ATU 1579. (doi:10.7592/FEJF2007.35.voolaid)
- Saul X. Levmore, Elizabeth Early Cook: Super strategies for puzzles and games. Doubleday and Company, Garden City, New York, 1981. ISBN 0-385-17165-X.
- Ian Pressman, David Singmaster: "The Jealous Husbands" and "The Missionaries and Cannibals". In: The Mathematical Gazette. Vol. 73, Nr. 464, 1989. S. 73–81. (JSTOR 3619658)
- Henry Ernest Dudeney: Amusements in Mathematics. 1917. (Amusements in Mathematics im Project Gutenberg )
-
- Benjamin L. Schwartz: An Analytic Method for the "Difficult Crossing" Puzzles. In: Mathematics Magazine. Vol. 34, Nr. 4, 1961. S. 187–193. (JSTOR 2687980)
- Robert Fraley, Kenneth L. Cooke, Peter Detrick: Graphical Solution of Difficult Crossing Puzzles. In: Mathematics Magazine. Vol. 39, Nr. 3, 1966. S. 151–157. (JSTOR 2689307)
- Péter Csorba, Cor A. J. Hurkens, Gerhard J. Woeginger: The Alcuin Number of a Graph. In: Algorithms: ESA 2008. Lecture Notes in Computer Science. Vol. 5193, Springer-Verlag, 2008. S. 320–331. (doi:10.1007/978-3-540-87744-8_27)
Weblinks
- Flussüberquerungen – Mathematische Basteleien