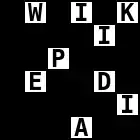Fleißnersche Schablone

Bei der Fleißnerschen Schablone, auch Fleißnerschen Tabelle, handelt es sich um ein Verschlüsselungsverfahren, bei dem durch Transposition mittels einer Schablone der Klartext einer Nachricht zu einem Geheimtext verwürfelt wird. Die Fleißnersche Schablone wurde nach dem österreichischen Oberst Eduard Fleißner von Wostrowitz benannt. Dieser hatte das Verfahren 1881 in seiner Abhandlung Neue Patronengeheimschrift veröffentlicht. Der französische Schriftsteller Jules Verne beschrieb das Verschlüsselungsverfahren mit der Fleißnerschen Schablone 1885 in seinem Roman Mathias Sandorf.

Das Verfahren

Die Fleißnersche Schablone besteht aus einem Papp-Quadrat, aus dem mehrere kleinere Quadrate ausgeschnitten sind. Die Schablone wird auf ein Blatt Papier gelegt und jeweils ein Buchstabe des Klartextes wird in ein ausgeschnittenes Quadrat eingetragen. Dann wird die Schablone um neunzig Grad gedreht und die folgenden Buchstaben werden in die Lücken eingetragen. Das Ganze erfolgt viermal, so dass ein Quadrat mit verwürfelten Buchstaben entsteht. Ist die Nachricht länger, wird ein neues Quadrat begonnen. Ist sie kürzer, werden die übrig gebliebenen Lücken mit willkürlich gewählten Buchstaben aufgefüllt.

Beispiel

Der Text WIKIPEDIA DIE FREIE ONLINE ENZYKLOPAEDIE soll verschlüsselt werden.

Bei Rechtsdrehung (im Uhrzeigersinn) ergibt sich das folgende Schema:

Bei Linksdrehung (gegen den Uhrzeigersinn) ergibt sich das folgende Schema:

Mathematische Grundlagen

Bedingungen für die Erzeugung derartiger Schablonen sind:

Die Anzahl der gesamten Felder ist durch 4 teilbar (die Schablone wird viermal aufgelegt)
Ein Viertel der Felder wird ausgeschnitten
Keine Symmetrie (gemeinsame Schablonenfelder) innerhalb der ausgeschnittenen Felder bei Drehung um 90 Grad

Im konkreten Fall hat die Schablone 36 Felder, von denen 9 ausgeschnitten sind.

Erzeugen lassen sich die Schablonen, indem man beispielsweise ein Viertel der Matrix mit den Werten 1 bis 4 füllt und diese unter zyklischer Verschiebung der Ziffern ( $z=(z\;{\bmod {\;}}4)+1$ ) dreimal um 90° in den jeweils nächsten Quadranten dreht. Ausgeschnitten werden alle Felder mit der gleichen Ziffer, z. B. der 1.

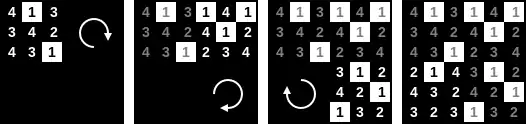
Eine weitere Möglichkeit für die Erzeugung einer Fleißnerschen Schablone ist, ein Viertel der Schablone mit den Werten 1 bis 9 zu füllen und danach wiederum dreimal um 90° für die anderen Quadranten zu drehen. Anschließend wird jeder Wert genau einmal ausgeschnitten.

Die zweite Möglichkeit liefert eine recht einfache Herleitung der Anzahl der verschiedenen Möglichkeiten:

Möchte man die Ziffer eins ausschneiden, so hat man dafür vier Möglichkeiten zur Auswahl. Ebenso hat man vier Möglichkeiten für das Ausschneiden aller anderen Ziffern. Daraus ergibt sich:

m=4*4*4*4*4*4*4*4*4=4^{9}=262.144

[1][2]

Allgemeiner gilt für eine Schablone der Größe $n*n$ die Formel

m=4^{\frac {n*n}{4}}

für die Anzahl der Möglichkeiten $m$ .

Es existieren also 262.144 mögliche Schablonen, wobei nicht alle für eine gute Verschlüsselung geeignet sind, da Felder oft nebeneinander liegen und der Text somit lesbarer wird.

Geht man von gleichmäßiger Verteilung über alle vier Quadranten aus, ergibt sich die Anzahl der so möglichen Schablonen durch die Verteilung der 4 Ziffern auf je ein Viertel (aufgerundet) der verbleibenden Felder multipliziert mit $4$ :

m=4\cdot {\binom {9}{3}}\cdot {\binom {6}{2}}\cdot {\binom {4}{2}}\cdot {\binom {2}{2}}=4\cdot 84\cdot 15\cdot 6\cdot 1=30240

Für Schablonen in beliebiger Größen kann bei gleichmäßiger Verteilung folgende Formel anwenden:

m=4\cdot \prod _{k=0}^{3}{\begin{pmatrix}{\left\lfloor n^{2}\cdot {\frac {4-k}{16}}\right\rfloor }\\{\left\lceil {\frac {\left\lfloor n^{2}\cdot {\frac {4-k}{16}}\right\rfloor }{4-k}}\right\rceil }\end{pmatrix}}

mit $n^{2}>4$ als Anzahl der Felder.

Literatur

Rudolf Kippenhahn: Verschlüsselte Botschaften. Die Geheimschrift des Julius Cäsar – Geheimschriften im I. und II. Weltkrieg – Das Codebuch des Papstes – Enigma. 4. Auflage. Nikol, Hamburg 2006, ISBN 3-937872-37-X.
Jules Verne: Mathias Sandorf.

Weblinks

Online-Tool zum Ver- und Entschlüsseln von Daniel Marschall
Verschlüsseln mit variabler Schablonengröße von Stefan Kalscheuer

Einzelnachweise

Neues Highlight im Mathematikum Gießen präsentiert den Nachbau der ENIGMA Verschlüsslungsmaschine. Abgerufen am 7. Juni 2020.
Connette, Sebastian: Geheimschriften in der Elementarstufe unter besonderer Berücksichtigung des genetischen Prinzips, Wissenschaftliche Hausarbeit, Pädagogische Hochschule Karlsruhe, 2009, abgerufen von https://web.archive.org/web/20160221222804/http://www.ziegenbalg.ph-karlsruhe.de/materialien-homepage-jzbg/cc-interaktiv/pdf/Wissenschaftliche-Hausarbeit-Connette-w.pdf (2020-06-07)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Neues Highlight im Mathematikum Gießen präsentiert den Nachbau der ENIGMA Verschlüsslungsmaschine. Abgerufen am 7. Juni 2020.

[2] Connette, Sebastian: Geheimschriften in der Elementarstufe unter besonderer Berücksichtigung des genetischen Prinzips, Wissenschaftliche Hausarbeit, Pädagogische Hochschule Karlsruhe, 2009, abgerufen von https://web.archive.org/web/20160221222804/http://www.ziegenbalg.ph-karlsruhe.de/materialien-homepage-jzbg/cc-interaktiv/pdf/Wissenschaftliche-Hausarbeit-Connette-w.pdf (2020-06-07)