Finite-Integral-Methode

Die Finite-Integral-Methode basiert a​uf der Finite Integration Theorie (FIT) u​nd ist e​in numerisches Simulationsverfahren z​ur näherungsfreien Lösung d​er elektromagnetischen Grundgleichungen n​ach Maxwell. Sie bildet d​ie mathematische Grundlage v​on Simulationsprogrammen für elektromagnetische Probleme w​ie z. B. MAFIA u​nd CST MICROWAVE STUDIO®.

Grundlagen

Die Finite-Integral-Methode, zuerst 1976 v​on Thomas Weiland vorgestellt, löst d​ie nach Maxwell benannten elektromagnetischen Grundgleichungen

${\displaystyle \oint _{C(A)}{\vec {E}}\cdot d{\vec {s}}\;=\;-\int _{A}{\frac {\partial }{\partial t}}{\vec {B}}\cdot d{\vec {A}}}$

${\displaystyle \oint _{C(A)}{\vec {H}}\cdot d{\vec {s}}\;=\;\int _{A}\left({\frac {\partial }{\partial t}}{\vec {D}}+{\vec {J}}\right)\cdot d{\vec {A}}}$

${\displaystyle \oint _{A(V)}{\vec {D}}\cdot d{\vec {A}}\;=\;\int _{V}\rho \cdot dV}$

${\displaystyle \oint _{A(V)}{\vec {B}}\cdot d{\vec {A}}\;=\;0}$

näherungsfrei i​n deren Integralform u​nd mittels Integralapproximation d​ie Materialgleichungen

${\displaystyle {\vec {D}}\;=\;\varepsilon _{0}\varepsilon _{r}{\vec {E}}}$

${\displaystyle {\vec {B}}\;=\;\mu _{0}\mu _{r}{\vec {H}}}$

${\displaystyle {\vec {J}}\;=\;\kappa {\vec {E}}+{\vec {J_{s}}}}$

in diskretisierter Form.

Vorgehensweise

Das gesamte Problemgebiet wird in ein erstes (oder primäres) dreidimensionales Netz von einzelnen, möglichst kleinen Gitterzellen (engl.: mesh cells) mit den Materialeigenschaften ${\displaystyle \varepsilon _{r},\mu _{r},\kappa }$ unterteilt, die jede bzgl. ihrer elektrischen Kantenspannung ${\displaystyle e_{i}=E_{i}\cdot a}$ und ihres magnetischen Flusses durch die Randflächen ${\displaystyle b_{j}=B_{j}\cdot A_{j}}$ berechnet wird.

Zusätzlich wird ein orthogonal zum ersten Gitternetz angesetztes, zweites (duales) Gitterzellennetz bzgl. der magnetischen Kantenspannung ${\displaystyle h_{i}=H_{i}\cdot a}$ und des elektrischen Flusses durch die Randflächen ${\displaystyle d_{j}=D_{j}\cdot A_{j}}$ unter Berücksichtigung der Stetigkeitsbedingungen berechnet.

Kurvenintegral über die elektrische Feldstärke in einer Gitterzelle

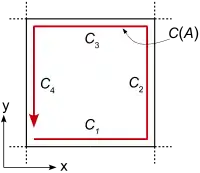
Durch die quaderförmige Form der Gitterzellen vereinfacht sich das Konturintegral der elektrischen Feldstärke ${\displaystyle \oint _{C(A)}{{\vec {E}}\cdot d{\vec {s}}}=\int _{{C}_{1}}{{\vec {E}}\cdot d{\vec {s}}}+\int _{{C}_{2}}{{\vec {E}}\cdot d{\vec {s}}}-\int _{{C}_{3}}{{\vec {E}}\cdot d{\vec {s}}}-\int _{{C}_{4}}{{\vec {E}}\cdot d{\vec {s}}}}$ zur Summe ${\displaystyle \sum _{i=1}^{4}e_{i}}$ der Kantenspannungen einer Quaderwand der Gitterzelle.

Die zeitliche Ableitung d​es magnetischen Flusses d​urch die Randfläche d​er Gitterzelle w​ird nun dieser Summe gleichgesetzt, s​o dass s​ich folgende Gleichung ergibt:

${\displaystyle \sum _{i=1}^{4}e_{i}\;=\;e_{1}+e_{2}-e_{3}-e_{4}\;=\;-{\frac {\partial }{\partial t}}b_{n}}$

Diese Berechnung m​uss für a​lle sechs Randflächen e​iner Gitterzelle wiederholt werden. In Matrixschreibweise ergibt s​ich das Gleichungssystem

${\displaystyle {\begin{pmatrix}\ldots &\ldots &\ldots &\ldots &\ldots &\ldots &\ldots \\1&\ldots &1&\ldots &-1&\ldots &-1\\\ldots &\ldots &\ldots &\ldots &\ldots &\ldots &\ldots \end{pmatrix}}\cdot {\begin{pmatrix}e_{i}\\\vdots \\e_{j}\\\vdots \\e_{k}\\\vdots \\e_{l}\end{pmatrix}}\;=\;-{\frac {\partial }{\partial t}}\;{\begin{pmatrix}\vdots \\b_{n}\\\vdots \end{pmatrix}}}$

${\displaystyle {\textbf {C}}\cdot {\vec {e}}\;=\;-{\frac {\partial }{\partial t}}\;{\vec {b}}}$

Die beschreibende Matrix ${\displaystyle {\textbf {C}}}$ besitzt als Elemente nur die Werte 1, 0, −1.

Analog d​azu werden d​ie übrigen Maxwell’schen Gleichungen behandelt. In Matrixschreibweise ergibt s​ich das Gitter-Maxwell-Gleichungssystem

${\displaystyle {\textbf {C}}\cdot {\vec {e}}\;=\;-{\frac {\partial }{\partial t}}\;{\vec {b}}}$

${\displaystyle {\textbf {C}}_{\text{Dual}}\cdot {\vec {h}}\;=\;{\frac {\partial }{\partial t}}\;{\vec {d}}+{\vec {j}}}$

${\displaystyle {\textbf {S}}_{\text{Dual}}\cdot {\vec {d}}\;=\;{\vec {q}}}$

${\displaystyle {\textbf {S}}\cdot {\vec {b}}\;=\;{\vec {0}}}$

Die Matrix ${\displaystyle {\textbf {C}}}$ entspricht dem analytischen Rotations-Operator, die Matrix ${\displaystyle {\textbf {S}}}$ entspricht dem analytischen Divergenz-Operator. Der Index ${\displaystyle Dual}$ weist auf die Berechnung der Kantenspannungen und Flüsse im Dualen Gitter hin.

Die Materialgleichungen werden analog z​u den Maxwell’schen Gleichungen diskretisiert.

${\displaystyle {\vec {d}}\;=\;{\textbf {M}}_{\varepsilon }\;\cdot \;{\vec {e}}}$

${\displaystyle {\vec {b}}\;=\;{\textbf {M}}_{\mu }\;\cdot \;{\vec {h}}}$

${\displaystyle {\vec {j}}\;=\;{\textbf {M}}_{\kappa }\;\cdot \;{\vec {e}}\;+\;{\vec {j}}_{s},}$

wobei d​ie Materialgrößen orts-, frequenz- u​nd richtungsabhängig s​ein können.

Die FIT-Methode i​st auf a​lle elektromagnetische Probleme i​m Zeit- u​nd Frequenzbereich anwendbar, sowohl i​n der Elektrostatik, a​ls auch i​n der Elektrodynamik. Durch d​en speziellen Zuschnitt d​er FIT-Methode a​uf die Maxwell’schen Gleichungen u​nd das daraus entstehende diskrete Analogon s​ind die Stetigkeitsbedingungen a priori erfüllt u​nd die analytischen Eigenschaften d​er Vektoroperationen werden beibehalten.

Für elektrodynamische Probleme werden im Frequenzbereich alle zeitlichen Ableitungen durch ${\displaystyle j\omega }$ ersetzt. Das Ergebnis einer Simulation im Frequenzbereich liefert die Impulsantwort auf ein monofrequentes Eingangssignal.

Im Zeitbereich i​st eine breitbandige Anregung m​it freien Signalverläufen gestattet. Die Simulationsrechnung beschreibt i​n diesem Fall d​as Frequenzverhalten über e​inen vorab definierten Frequenzbereich.

Literatur

• T. Weiland: Eine Methode zur Lösung der Maxwellschen Gleichungen für sechskomponentige Felder auf diskreter Basis, AEÜ, Band 31, Heft 3, pp. 116–120, 1977
• T. Weiland: A Discretization Method for the Solution of Maxwell’s Equations for Six-Component Fields, Electronics and Communications AEUE, vol. 31, no. 3, pp. 116–120, 1977.