Filter-Transformation

Die Filter-Transformation dient im Rahmen des Filterentwurfes dazu, elektronische Filter zwischen verschiedenen Filtertypen wie Tiefpassfilter, Hochpassfilter oder Bandpassfilter umzusetzen.

Allgemeines

Elektronische Filter werden anhand einer gewünschten Übertragungsfunktion H(s) konzipiert. Beispiele von üblichen Übertragungsfunktionen, welche insbesondere bei analogen, zeitkontinuierlichen Filtern in verschiedenen Filterordnungen eingesetzt werden, stellen die Butterworth-Filter, Tschebyscheff-Filter, Bessel-Filter oder auch Cauer-Filter dar.

Zur Dimensionierung wird von einem allgemeinen Prototypfilter üblicherweise in der Form eines normierten Tiefpassfilters ausgegangen. Bei der Normierung, sie dient dazu den Filterentwurf unabhängig von konkreten Frequenzwerten zu gestalten, werden alle frequenzabhängigen Parameter auf die Grenzfrequenz des Prototypenfilters bezogen. In dieser vereinfachten Form lassen sich die Filterparameter der Übertragungsfunktion, sie werden bei analogen Filtern durch die Werte von elektrischen Bauelementen wie Widerständen, Kondensatoren und Spulen beschrieben, in Form von Tabellen allgemein angeben bzw. in Datenbanken speichern.[1]

Für die Realisierung eines konkreten Filters in Form einer elektrischen Schaltung wird eine Entnormierung des dimensionierten Prototypfilters und die Filter-Transformation in den endgültigen Filtertyp vorgenommen. Da als Prototypfilter in den Filtertabellen meist Tiefpässe verwendet werden, ist insbesondere die Transformation von dem Tiefpass zu dem Hochpass und den Bandpass bzw. der Bandsperre von Bedeutung. Die Transformation kann aber, wie jede Transformation, auch in umgekehrter Richtung erfolgen. Die Filter-Transformationen werden in adaptierter Form ebenfalls im Rahmen von zeitdiskreten Digitalfiltern eingesetzt. Insbesondere wenn analoge Filterschaltungen im Rahmen der digitalen Signalverarbeitung nachgebildet werden, wie beispielsweise bei den Wellendigitalfiltern.

Tiefpass-Hochpass-Transformation

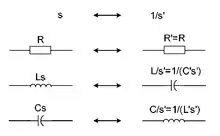
Eigenschaften der TP-HP Transformation

Die Tiefpass-Hochpass-Transformation (TP-HP) dient dazu einen beliebigen Tiefpass in einen Hochpass umzuwandeln. Dabei wird aus der Übertragungsfunktion des Tiefpasses H_TP(s) die Übertragungsfunktion H_HP(s′) durch folgende Substitution gebildet:

s'={\frac {1}{s}}

mit s=jω bzw. s′=jω′ als Parameter der Kreisfrequenz. In der elektrischen Schaltung bedeutet diese Umsetzung, dass die normierten Bauelemente wie Kondensatoren C und Spulen L, welche die Pol- bzw. Nullstellen charakterisieren, wechselseitig vertauscht werden:

R=R',\qquad L={\frac {1}{C'}},\qquad C={\frac {1}{L'}}

Tiefpass-Bandpass-Transformation

Eigenschaften der TP-BP Transformation

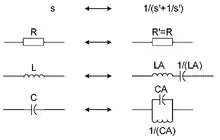
Die Tiefpass-Bandpass-Transformation (TP-BP) dient dazu einen beliebigen Tiefpass in einen Bandpass umzuwandeln. Dabei wird der Betragsfrequenzgang des Tiefpassfilters in logarithmischen Frequenzmaßstab an der Mittenfrequenz des Bandpasses gespiegelt. Damit wird durch die TP-BP-Transformation die Ordnung verdoppelt und es sind nur symmetrische Bandpässe mit gerader Filterordnung möglich.

Aus der Übertragungsfunktion des Tiefpasses H_TP(s) wird mit folgender Transformation die Übertragungsfunktion H_BP(s′) gebildet:

s'={\frac {1}{2\pi B}}\left(s+{\frac {1}{s}}\right)

mit dem Parameter B welcher die Bandbreite des Bandpasses beschreibt. In der elektrischen Schaltung bedeutet diese Umsetzung, wie in nebenstehender Abbildung dargestellt, dass die normierten Kondensatoren C des Tiefpasses in Reihenschwingkreise und Spulen L in Parallelschwingkreise im Bandpassfilter realisiert werden.

Für unsymmetrische Bandpässe existieren spezielle Transformationen wie die Zdunek-Filtertransformation.[2]

Tiefpass-Bandsperre-Transformation

Die Tiefpass-Bandsperre-Transformation (TP-BS) kann als eine Kombination der TP-HP und TP-BP-Transformation betrachtet werden: Die Anwendung der TP-BP-Transformation auf einen Hochpass ergibt eine Bandsperre.

Zusammengefasst aus der Übertragungsfunktion des Tiefpasses H_TP(s) wird mit folgender Transformation die Übertragungsfunktion H_BS(s′) der Bandsperre gebildet, der Parameter B der Bandbreite ist identisch wie bei der TP-BP-Transformation:

s'={\frac {2\pi B}{\left(s+{\frac {1}{s}}\right)}}

Literatur

Ulrich Tietze, Christoph Schenk: Halbleiter-Schaltungstechnik. 12. Auflage. Springer, Berlin 2002, ISBN 3-540-42849-6.
Fred H. Irons: Active Filters for Integrated-Circuit Applications. Artech House, 2005, ISBN 1-58053-896-7.

Einzelnachweise

Rudolf Saal, Walter Entenmann: Handbuch zum Filterentwurf. 2. Auflage. Hüthig, 1988, ISBN 3-7785-1558-6 (Filtertabellen).
W. Winkelnkemper: Unsymmetrical bandpass and bandstop digital filters. IEEE Electronics Letters, 5, 23. Ausgabe, 1969, S. 585 bis 586 (ieee.org [PDF]).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Rudolf Saal, Walter Entenmann: Handbuch zum Filterentwurf. 2. Auflage. Hüthig, 1988, ISBN 3-7785-1558-6 (Filtertabellen).

[2] W. Winkelnkemper: Unsymmetrical bandpass and bandstop digital filters. IEEE Electronics Letters, 5, 23. Ausgabe, 1969, S. 585 bis 586 (ieee.org [PDF]).