Endspieldatenbank
Endspieldatenbanken (umgangssprachlich aus Englisch auch tablebase genannt) verfügen über vollständiges Endspielwissen zu Schachstellungen mit wenigen Steinen. Es gibt inzwischen Endspiel-DVDs mit nahezu allen Stellungstypen bis zu sechs Steinen, beispielsweise liegt das wichtige Turmendspiel „König, Turm und zwei Bauern gegen König und Turm“ vollständig analysiert vor. Eine Abfrage der Datenbank zeigt hierzu in jeder Stellung, ob bei beiderseits bestem Spiel Weiß oder Schwarz gewinnt und welches der „beste“ Zug ist, oder ob die Stellung remis ist und welche Züge das Remis erhalten.
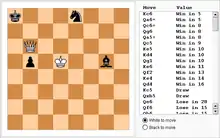
Im Jahre 2012 meldete die Universität Moskau, dass die Datenbanken mit sieben Steinen vollständig erstellt sind. Sie umfassen ca. 140 Terabyte.[1]
Grundlagen
Es gibt verschiedene Möglichkeiten, ein Ziel für eine bestimmte Position festzulegen. Der US-amerikanische Informatiker Ken Thompson hat das Matt und den Übergang in ein anderes gewonnenes Endspiel (durch Schlagen einer Figur oder durch Umwandlung) als gleichwertig festgelegt. In einer Position Dame gegen Turm (ohne weitere Figuren) war für ihn das Schlagen des Turmes (ohne nachfolgenden Damenverlust) als Teilziel so gut wie das sofortige Matt. Heutzutage (von Nalimov und zuvor auch anderen Entwicklern festgelegt) ist das Matt in der kürzesten Anzahl von Zügen das Ziel, entweder mit oder ohne Beachtung der 50-Züge-Regel.
Abgesehen von Programmierfehlern und kleinen Ausnahmen sind die Ergebnisse der durch Computer erzeugten Endspieldatenbanken vollständig und fehlerfrei. Die Möglichkeit von Programmierfehlern kann nahezu ausgeschlossen werden, weil viele Endspiele auf verschiedene Art bereits berechnet und die Ergebnisse gegenseitig geprüft worden sind. Eine Ausnahme bildet aber zum Beispiel die Rochade, welche in den meisten Fällen in Endspieldatenbanken keine Beachtung findet.
Durch Endspieldatenbanken konnte die im Laufe von Jahrhunderten der Schachentwicklung gewachsene Endspieltheorie präzisiert werden. Bei den Fünfsteinern war bemerkenswert, dass das bis dahin als remis betrachtete Endspiel „König und zwei Läufer gegen König und Springer“ im Allgemeinen gewonnen werden kann. Allerdings gibt es Stellungen, in denen erst nach 66 Zügen das Matt zu erzwingen ist. Dies kollidiert mit der aus praktischen Aspekten festgeschriebenen 50-Züge-Regel, so dass solche Stellungen bei beiderseits bestem Spiel in einer Schachpartie letztendlich doch remis ausgehen, obwohl Matt unvermeidbar wäre.
Mittlerweile wurden in neueren Endspielbüchern (z. B. durch John Nunn und in den zwei prinzipiellen Werken von Frank Lamprecht und Karsten Müller) die Unzulänglichkeiten aus klassischen Werken von André Chéron, Juri Awerbach, Max Euwe und Reuben Fine korrigiert, präzisiert und vervollständigt.
Während einer praktischen Partie am Brett spielen die Endspieldatenbanken (besonders für diese langzügigen Endspiele) keine Rolle. Zum einen ist fremde Hilfe während der Partie untersagt. Zum anderen können selbst die besten Spieler in komplizierteren Stellungen nicht so exakt spielen. Das kann z. B. in einem Damenendspiel „Dame und Bauer gegen Dame“ beobachtet werden, wenn man den Partieverlauf mit einer Endspieldatenbank prüft. Bedenkzeitverknappung und Abschaffung von Hängepartien haben zu Qualitätsminderung in der Endspielphase bei Schachpartien geführt.
Verwendet werden können Endspieldatenbanken im Fernschach, bei Partieanalysen, beim Nachweis der Korrektheit von Studien oder Mehrzügern in der Schachkomposition und in Schachprogrammen.
Herstellungsverfahren
Im großen Maßstab hat Ken Thompson an den Bell Laboratories mit einem Computerprogramm Endspieldatenbanken unter schachlicher Beratung von John Roycroft erstellt. Allerdings gab es bereits früher Arbeiten auf begrenzten Teilgebieten durch Ströhlein, Zagler und in der Sowjetunion. Zu diesem Zeitpunkt waren Computer noch zu teuer, um weite Verbreitung zu finden. Erst als sich nach einiger Zeit die Möglichkeit ergab, Thompsons Ergebnisse auf CD weiterzugeben und zu nutzen, fanden sie Aufmerksamkeit in breiteren Kreisen der Schachspieler.
Der Algorithmus zur Erstellung wurde bereits 1912 von Ernst Zermelo auf einem Mathematikerkongress publiziert. Später fand er sich als Spezialfall in der mathematischen Spieltheorie wieder. Dieses Verfahren der retrograden Analyse ist relativ einfach in vier Schritten zu beschreiben:
Schritt 1: Erzeugen aller möglichen Stellungen mit nicht mehr als n Steinen
Für alle zulässigen Stellungen mit höchstens n Steinen wird in einer Datei ein Index reserviert. Diese Datei war bei Thompson (für n = 5) mehrere Gigabyte groß.
Schritt 2: Ermitteln aller Gewinnstellungen für Weiß
- Suche alle Stellungen, bei denen Schwarz matt ist. Markiere diese Stellungen in der Datei.
- Suche alle Stellungen, bei denen Weiß am Zug ist und Weiß mindestens einen Zug hat, der zu einer Stellung unter 1. führt. Das sind alle Stellungen, in denen Weiß mit einem Zug matt setzen kann. Markiere diese Stellungen in der Datei.
- Suche alle Stellungen, bei denen Schwarz am Zug ist und jeder Zug von ihm zu einer Stellung unter 2. führt. Schwarz kann hier Matt in einem Zug nicht verhindern. Markiere diese Stellungen in der Datei.
- Suche alle Stellungen, bei denen Weiß am Zug ist und Weiß mindestens einen Zug hat, der zu einer Stellung unter 3. führt. Das sind alle Stellungen, in denen Weiß mit 2 Zügen matt setzen kann. Markiere diese Stellungen in der Datei.
- Suche alle Stellungen, bei denen Schwarz am Zug ist und jeder schwarze Zug zu einer Stellung unter 4. oder 2. führt. Schwarz kann hier Matt in 2 Zügen nicht verhindern. Markiere diese Stellungen in der Datei.
- Suche alle Stellungen, bei denen Weiß am Zug ist und Weiß mindestens einen Zug hat, der zu einer Stellung unter 5. führt. Das sind alle Stellungen, in denen Weiß mit 3 Zügen matt setzen kann. Markiere diese Stellungen in der Datei.
- usw.
Irgendwann bricht dieses Verfahren ab, weil in einem Schritt die neu zu bildende Menge von Stellungen leer bleibt und so auch keine weiteren nichtleeren Mengen erzeugt werden können. Dann sind alle Stellungen gefunden, in denen Weiß gewinnt. Weiter mit Schritt 3.
Schritt 3: Ermitteln aller Gewinnstellungen für Schwarz
Diese Stellungen findet man nach dem gleichen Verfahren wie unter Schritt 2.
Schritt 4: Die restlichen Stellungen sind remis.
Die verbleibenden Stellungen können weder von Weiß noch von Schwarz gewonnen werden. Es sind also Remis-Stellungen.
Das heutzutage verwendete Verfahren von Nalimov umfasst einige Verbesserungen technischer Art. Der vorgestellte Algorithmus bleibt prinzipiell gleich.
Theoretisch kann man so das gesamte Schachspiel vollständig analysieren, indem man das Verfahren auf 32 Steine erweitert. Praktisch ist das aber gegenwärtig noch nicht möglich, weil mit jedem zusätzlichen Stein die Anzahl der Stellungen und damit die Rechenzeit drastisch zunimmt. Ungeachtet dieser Tatsache wird mit Hilfe von leistungsfähigen Rechnern weiter an entsprechenden Analysen gearbeitet. Ende des Jahres 2002 waren bereits alle Stellungen mit maximal fünf Figuren erfasst und analysiert, Stellungen mit sechs Figuren sind seit August 2005 fertig. Seit Frühjahr des Jahres 2006 lagen erste Ergebnisse von Stellungen mit sieben Steinen (ohne Bauern) vor. Inzwischen kann man alle Endspielstellungen mit bis zu fünf Steinen sowie die wichtigsten Sechssteiner im Syzygy-Format auf handelsüblichen DVDs erwerben. Die Tabellen können auf Festplatten oder Solid-State-Drives abgelegt werden und gestatten es modernen Schachprogrammen, wie Komodo, Deep Fritz, Houdini und Stockfish, die Daten auch während der Laufzeit des Programms zu nutzen, was zu einer wesentlichen Steigerung der Spielstärke im Endspiel auch bei mehr als sechs Steinen führt.
Im Jahre 2012 meldete die Universität Moskau, dass die Datenbanken mit sieben Steinen vollständig erstellt sind. Derzeit werden die Daten in ein Format importiert, welches von Schachprogrammen benutzt werden kann. Man schätzt, dass die vollständigen Sieben-Steine-Datenbanken ca. 140 Terabyte umfassen.[1]
Metriken
Endspieldatenbanken gibt es in mehreren Metriken. In der DTM-Metrik (Depth to Mate, also Tiefe zum Matt) wird die Entfernung gespeichert, die bei längstem gegnerischen Gegenspiel zum Matt benötigt wird. Dabei wird jedoch die 50-Züge-Regel nicht berücksichtigt. Aus diesem Grund wurden Datenbanken mit den Metriken DTC (Depth to Conversion, also Tiefe bis zur Veränderung) und DTZ (Depth to Zero, also Tiefe bis Null) geschaffen. Daraus ging dann die DTZ-50-Metrik hervor, die die 50-Züge-Regel berücksichtigt. Bei DTC wird die Entfernung gespeichert, die von einer bestimmten Stellung zu einer Umwandlung oder einem Schlagfall benötigt wird.
Nutzen
Dem Schachspieler sind bei der direkten Nutzung der neueren Forschungen auf eigenem Computer durch Größe und Vielzahl der Dateien und des damit benötigten Datenträger-Platzes Grenzen gesetzt. Es gibt aber im Internet spezielle Server, bei denen sich durch Anfragen Ergebnisse einer konkreten Endspielposition ermitteln lassen. Thompson gab seine Ergebnisse Interessenten zum Herstellungspreis der CD ab, bei einer Firma waren diese vier CDs mit Stellungen bis fünf Steinen und höchstens einem Bauern käuflich erwerbbar. Thompson komprimierte seine Daten mit dem Huffman-Verfahren, um überhaupt für die Abfrage mit einer CD auskommen zu können. Diese Entscheidung erwies sich als hinderlich bei der Weiterentwicklung und Optimierung von Schachprogrammen.
Bei einem Schachprogramm mit aktivierter Endspieldatenbank bemerkt man im Endspiel eine deutlich höhere Zugfrequenz, da der Computer nun weniger rechnet und häufiger in seiner Endspieldatenbank nachzusehen hat, ähnlich dem Suchen bereits früher berechneter Stellungen in seiner Hashtabelle.
50-Züge-Regel
Die für praktische Schachpartien sinnvolle 50-Züge-Regel erschwert gerade in Endspielen mit Bauern die Computerberechnung extrem. Entweder ignoriert das Programm die Remis-Regel und geht direkt auf Matt, oder es wird in erster Linie der Bauer gezogen, was aber zu einer wesentlich längeren Variante führen kann, auch in Stellungen, die unter 50 Zügen matt sind. Die richtige Lösung muss alle Endspiele weiter unterteilen mit den exakten Bauernpositionen wie „König, Dame und Bauer auf der 5. Reihe gegen König und Dame“. Sobald der Bauer zieht, ist die 50-Züge-Regel unterbrochen und das Endspiel übernimmt die Anzahl Züge vom Endspiel mit Bauer auf der 6. Reihe, das schon berechnet sein muss, und so fort. Die Anzahl der dadurch gewonnenen Stellungen wird aber kaum vom direkten Mattweg abweichen, sodass der praktische Nutzen für das viel komplexere Verfahren zu gering erscheint.
1. Beispiel:
| a | b | c | d | e | f | g | h | ||
| 8 | 8 | ||||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h |
Für dieses konkrete Beispiel zeigt die Endspieldatenbank, dass unter Missachtung der 50-Züge-Regel und bei beiderseitigem optimalen Spiel Weiß nach 65 Zügen zwingend matt setzt. Es handelt sich um ein Endspiel „Turm und Läufer gegen Turm“. Gemäß 50-Züge-Regel ist dieses Endspiel bei bester schwarzer Verteidigung remis. Dieser Endspieltyp führte dazu, dass die FIDE die 50-Züge-Regel zeitweise durch eine 100-Züge-Regel ersetzte.
Großmeister Edmar Mednis hat die Datenbanklösung dargestellt und den Verlauf ausführlich kommentiert. Allerdings bezieht er sich auf Untersuchungen von Ken Thompson auf dem Computer Belle im Jahre 1986. Diese findet im 55. Zug nicht die beste schwarze Verteidigung und endet bereits nach 59 Zügen mit Matt.[2]
2. Beispiel:
Bei den Siebensteinern sind Stellungen bekannt, die in über 500 Zügen zum Matt führen.[3]
Schachkomposition
Endspieldatenbanken können verwendet werden, um orthodoxe Probleme und Studien zu überprüfen. Durch die Widerlegung falscher Annahmen kann so auch eine große Anzahl von Studien inkorrekt werden. Ein Beispiel dafür sind Studien, in denen angenommen wurde, dass zwei Läufer gegen einen Springer normalerweise nur remisieren könnten. Jedoch kann blindes Vertrauen auf die Datenbank zu falschen Ergebnissen führen, etwa wenn ein Datenbankzug zwar schneller ist, aber erst später in die Lösung des Autors einmündet, der nicht immer den längsten Widerstand vorsieht, sondern den, bei dem Weiß nur einen möglichen Gewinnzug hat.
Beim Kongress der Ständigen Kommission für Schachkomposition bei der FIDE in Rhodos 2007 wurde festgelegt, dass eine Endspieldatenbank Schachkompositionen nicht vorwegnimmt.[4]
Beispiele:
Deutsche Schachblätter 1938
| a | b | c | d | e | f | g | h | ||
| 8 | 8 | ||||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h |
Weiß zieht und gewinnt
Schachmaty w SSSR 1946
| a | b | c | d | e | f | g | h | ||
| 8 | 8 | ||||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h |
Links: Die Datenbank zeigt, dass neben Heuäckers Lösung 1. Lf6+ Ke8 2. Lg2 Kd7 3. Le5 Sg4 4. Lh3 Ke6 5. Lf4 Kf5 6. Lc1 d3 7. Ld2 auch 1. Lxd4 gewinnt – ein Zug, der nicht von Heuäcker übersehen, sondern damals falsch eingeschätzt wurde, da das Endspiel von zwei Läufern gegen einen Springer vor der Berechnung der entsprechenden Datenbanken auch aufgrund einer vermeintlichen Festung als remis galt.
Rechts: Die Datenbank bestätigt, dass nur Gasparjans Lösung 1. Ka2!! Th3 2. Kb2 Tg3 3. Kc2 Th3 4. Kd2 Tg3 5. Ke2 Th3 6. Kf2 gewinnt.
Endspieldatenbanken für verwandte Spiele
Schach wurde auf den Brettern 3 × 3 und 3 × 4 vollständig gelöst.[5] Das Damespiel befindet sich noch in der Erforschung, jedoch wurden die besten praktischen Spielverläufe in der Variante Checkers gelöst.[6] Zu weiteren Spielen siehe den Artikel „Gelöste Spiele“.
Siehe auch
Literatur
Grundlagen der Endspieldatenbanken
- Christian Posthoff, Günter Reinemann: Computerschach – Schachcomputer. Akademie-Verlag, Berlin, 1987. ISBN 3-05-500228-8.
- Christian Posthoff, Rainer Staudte, Michael Schlosser: Optimale Strategien. Schach-Report, 1993, Heft 7, Seite 41–46.
Präzisierung der Theorie durch Endspieldatenbanken
- John Nunn: Secrets of Rook Endings. B. T. Batsford Ltd, London 1992. ISBN 0-7134-7164-6.
- John Nunn: Secrets of Pawnless Endings. B. T. Batsford Ltd, London 1994. ISBN 0-7134-7508-0.
- John Nunn: Secrets of Minor Piece Endings. B. T. Batsford Ltd, London 1995. ISBN 0-7134-7727-X.
Weblinks
- online Endspieldatenbankabfrage Alle 5-Steiner (deutsch)
- online Endspieldatenbankabfrage Alle 6-Steiner (deutsch)
- online Endspieldatenbankabfrage, Metriken DTM, DTC, DTZ, DTZ50 Alle 5- und die meisten 6-Steiner (englisch)
- Endgame Tablebases für emule Alle 6-Steiner (englisch)
- Syzygy endgame tablebases Interaktive Nutzung für alle 7-Steiner (englisch)
Einzelnachweise
- Lomonosov Endgame Tablebases (abgerufen am 9. August 2018).
- Schach-Report 1995/4, S. 44–48.
- Lomonosov Table Bases, eingesehen am 4. August 2021
- PCCC meeting 2007. Minutes. Absatz 8.8 (englisch) (DOC-Datei; 99 kB)
- http://kirr.homeunix.org/3x3-chess/ und http://kirr.homeunix.org/chess/3x4-chess/
- Archivierte Kopie (Memento des Originals vom 24. Juni 2003 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.