Dynamic-Time-Warping
Dynamische Zeitnormierung (engl. dynamic time warping) bezeichnet einen Algorithmus, der Wertefolgen unterschiedlicher Länge aufeinander abbildet.[1]
Anwendung
Ein prominentes Anwendungsbeispiel ist die Spracherkennung (das Erkennen von Sprechmerkmalen beim Diktieren): Hier sollen durch den Vergleich mit gespeicherten Sprachmustern einzelne Wörter aus einem gesprochenen Text erkannt werden. Ein Problem besteht darin, dass die Wörter oft unterschiedlich ausgesprochen werden. Vor allem Vokale werden oft länger oder kürzer gesprochen, als es im gespeicherten Sprachmuster der Fall ist: das Wort „heben“ zum Beispiel kann einmal mit kurzem „e“ und ein anderes mal wie „heeeben“ ausgesprochen werden. Für einen erfolgreichen Mustervergleich sollte das Wort also entsprechend gedehnt bzw. gestaucht werden, jedoch nicht gleichmäßig, sondern vor allem an den Vokalen, die länger bzw. kürzer gesprochen wurden. (In geringerem Maße gilt dies übrigens auch für Konsonanten, auch können bestimmte Laute komplett verschluckt werden.) Der Dynamic-time-warping-Algorithmus leistet diese adaptive Zeitnormierung.[1][2]
Weitere Anwendungsbereiche des dynamic time warping sind z. B. Gestenerkennung in der Bildbearbeitung oder Messungen bei korreliertem Rauschen in der Physik.[3]
Algorithmus
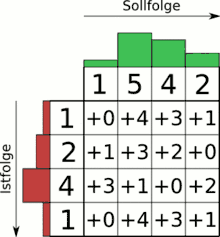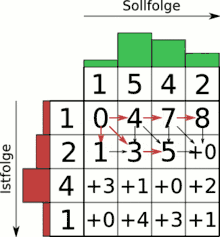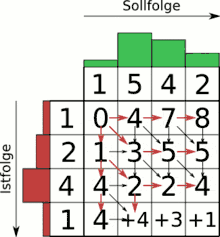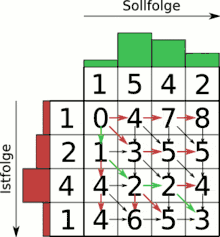
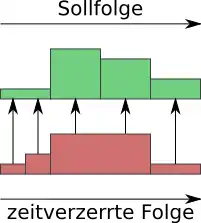
Der Algorithmus findet z. B. bei der Spracherkennung Anwendung. Ein gesprochenes Sprachsignal soll mit einer Menge existierender Schablonen (engl. Templates) abgeglichen werden, um das gesprochene Wort wiedererkennen zu können und beispielsweise auf einem Mobiltelefon eine entsprechende Aktion auszuführen. Sprachsignale werden dabei üblicherweise als spektrale bzw. cepstrale Wertetupel abgespeichert, die mit weiteren Stimminformationen wie Intensität usw. als Merkmalsvektoren ergänzt sind.
Mit Hilfe einer Gewichtungsfunktion für die einzelnen Parameter jedes Wertetupels kann ein Differenzmaß zwischen zwei beliebigen Werten der beiden Signale aufgestellt werden (Kostenfunktion), beispielsweise eine normalisierte euklidische Distanz oder die Mahalanobis-Distanz.[4]
Der Algorithmus sucht nun den „kostengünstigsten“ Weg vom Anfang zum Ende beider Signale über die aufgespannte Matrix der paarweise vorliegenden Kosten aller Punkte beider Signale. Dies geschieht mit Hilfe der dynamischen Programmierung effizient. Den tatsächlichen Pfad, also das Warping, erhält man durch das sogenannte Backtracking nach dem ersten Durchlauf des Algorithmus. Für die reine Kostenbestimmung (also die Templateauswahl) reicht allerdings der einfache Durchlauf ohne Backtracking. Das Backtracking ermöglicht hierbei also eine genaue Abbildung jedes Punktes des kürzeren Signales auf einen oder mehrere Punkte des längeren Signales und stellt damit die ungefähre Zeitverzerrung dar.
Aufgrund algorithmischer Probleme bei der Extraktion von Sprachsignalparametern (Oktavfehler, Stimmaktivierungsfehler etc.) muss der optimale Pfad durch die Signaldifferenzmatrix nicht unbedingt der tatsächlichen Zeitverzerrung entsprechen.
Einzelnachweise
- DTW oder dynamic time warping. www.inf.fu-berlin.de. Abgerufen am 8. April 2009.
- Wendemuth, Andreas: Grundlagen der stochastischen Sprachverarbeitung, S. 137
- Wendemuth, Andreas: Grundlagen der stochastischen Sprachverarbeitung, S. 133
- Black, A. W.; P. Taylor (1997a): Automatically clustering similar units for unit selection in speech synthesis. In: Proc. Eurospeech ’97.