Deontische Logik

Deontische Logik ist der Bereich der Logik, der die logischen Verhältnisse von Begriffen, die sich auf das Sollen beziehen, untersucht. Begriffe, die sich auf das Sollen beziehen, sind Gebot (Pflicht), Verbot, Erlaubnis und andere mehr.

Etymologisch entstammt der Ausdruck aus dem altgriechischen δέον déon (Gen. δέοντος déontos). "to déon" wird verschieden übersetzt: unter anderem mit das Nötige, das Angemessene, das "Erforderliche", "das Notwendige", die "Pflicht".

Als Gegenbegriff wird vereinzelt der Terminus ontische Logik gebildet[1]. "Ontische Logik" ist dann die Logik der Sätze (nur) über das Sein (siehe zur Seinslehre auch Ontologie).

Sätze über das Sein haben in der (zweiwertigen) Logik die Wahrheitswerte wahr oder nicht wahr (falsch). Sätze über das Sollen sind nicht wahr oder falsch, sondern gültig oder nicht gültig (ungültig)[1].

Zu beachten ist der Unterschied zwischen einer Norm und einem Normsatz: "Normen gebieten, verbieten oder erlauben ein bestimmtes Verhalten, Normsätze behaupten demgegenüber, daß ein bestimmtes Verhalten geboten, verboten oder erlaubt sei."[2]. Je nach dem Zusammenhang kann derselbe Satz eine Norm oder einen Normsatz ausdrücken. Mit dem Satz "Mord ist verboten" kann das Verbot des Mordes (Norm) oder die Behauptung, dass Mord verboten sei, gemeint sein (Normsatz)[3]. Ein Normsatz als Behauptung über eine Norm kann wahr oder falsch sein[1].

Die deontische Logik ist eine formale, philosophische, nichtklassische Logik. Sie wird als Anwendungsfall der Modallogik, als "Modallogik im weiteren Sinn" oder (nur) als Logik in Anlehnung an die Modallogik betrachtet.

Wie die ontische Logik wird die moderne deontische Logik formalisiert und wenn möglich kalkülisiert betrieben. Über die dabei zugrunde zu legenden deontischen (deontologischen) Grundbegriffe bestehen unterschiedliche Ansichten.

Deontische Grundbegriffe

Deontische Grundbegriffe sind geboten und verboten.

Eine Beschränkung hierauf würde bedeuten, dass alles, was nicht geboten ist, verboten wäre.

Von Aristoteles wird angenommen, dass er für eine konkrete Handlung annahm, dass diese entweder geboten oder verboten sei.

Die (allgemeine) Modallogik kennt drei Grundbegriffe und deren Negationen: notwendig/unnotwendig, unmöglich/möglich kontingent/nicht kontingent. In Analogie dazu wird von drei deontischen Grundbegriffen und ihrer Verneinung ausgegangen: geboten/ungeboten, verboten/unverboten und indifferent/nicht indifferent[4].

Statt indifferent spricht man auch von "freigestellt".

Betont wird, dass "erlaubt" (mindestens) zwei verschiedene Bedeutungen haben kann: zum einen als "nicht verboten" (von einem bestimmten Verbot): relativ erlaubt (unverboten), was nicht ausschließt, dass etwas geboten ist. Erlaubt kann auch in einem absoluten Sinn gemeint sein, d. h. etwas ist weder verboten noch geboten: indifferent[4].

Syntax

Die formalisierte deontische Logik benutzt sprachliche Zeichen zur Abkürzung der deontischen Grundbegriffe, die deontische Operatoren genannt werden. Diese können von Sprache zu Sprache und innerhalb einer Sprache von Autor zu Autor verschieden sein. Verbreitet sind:

Es ist geboten: O (von obligatory);
Es ist verboten: V, auch F (von forbidden);
Es ist erlaubt: E, auch P (von permitted);
Es ist freigestellt: I.

Das ermöglicht beispielsweise folgende atomare deontische Sätze:

Für "Es ist geboten, die Handlung p zu tun", kann man formalisiert "O (p)" schreiben.
Für "Es ist geboten, dass das Individuum a die Handlung p tut, kann man "O (p (a))"[5] schreiben.

Veranschaulichungen

Die Beziehungen der deontologischen Grundbegriffe werden unterschiedlich dargestellt. Zum einen als logische Quadrate oder als deontologisches Sechseck-

logisches Quadrat

Das logische Quadrat

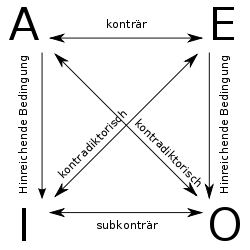
Stellt man die Beziehungen als deontisches logisches Quadrat ("Normenquadrat"[6]) dar, so ist zu beachten, dass ein Gebots- und ein Erlaubnisquadrat zu unterscheiden ist.

Beim Gebotsquadrat steht "A" für Gebot (O), "E" für Verbot (F), "I" für Erlaubnis und O für "Es ist nicht geboten"[7].

Beim Erlaubnisquadrat steht "A" für "¬ P (¬ p)", "E" für "¬ P (p)", "I" für "P (p)" und "O" für "P (¬ p)"[8].

(Übersetzt: "Ist nicht erlaubt, dass nicht p" ("A") ist kontradiktorisch zu "Es ist erlaubt, dass p" ("O"). "A" enthält "subaltern" "I", d. h. "Es ist erlaubt, dass p". "I" ist kontradiktorisch zu "E", d. h. "Es ist nicht erlaubt, dass p". "A" und "E" sind konträr, d. h. schließen sich aus. Es kann nicht zugleich sein, dass p nicht erlaubt ist ("E") und dass es nicht erlaubt ist, dass nicht p ist ("A").)

deontologisches Sechseck

Analog zur Modallogik kann für die drei Grundbegriffe und ihre Negationen auch ein deontologisches Sechseck zur Veranschaulichung der Beziehungen der Grundbegriffe zugrunde gelegt werden[9]

Operatorenäquivalenzen

Wie in der Modallogik gibt es Operatorenäquivalenzen:

Beispiel: F (p) ↔ O (¬ p)

"Genau dann, wenn es verboten ist, die durch p beschriebene Handlung zu vollziehen, ist es geboten, die durch p beschriebene Handlung nicht zu vollziehen = Das Verbot entspricht dem Gebot der Unterlassung."[10]

Beispiel: O (p) ↔ F (¬ p)

"Genau dann, wenn es geboten ist, die durch p beschriebene Handlung zu vollziehen, ist es verboten, die durch p beschriebene Handlung nicht zu vollziehen = Das Gebot entspricht dem Verbot der Unterlassung."[10]

Geschichte

Frühe Deontische Logik

Philosophen der indischen Mimamsa Schule und der Alten Griechen bemerkten die formalen logischen Relationen der deontischen Konzepte[11]. Philosophen des späten Mittelalters verglichen deontische Konzepte mit alethischen.[12] In Elementa juris naturalis bemerkte Leibniz, die logischen Relationen zwischen licitum (erlaubt), illicitum (verboten), debitum (geboten) und indifferens (egal) seien äquivalent zu denen zwischen possibile (möglich), impossibile (unmöglich), necessarium (notwendig) und contingens (kontingent).

Mallys erste Deontische Logik

Ernst Mally, ein Schüler von Alexius Meinong, war der erste, der ein formales System der deontischen Logik in Grundgesetze des Sollens vorschlug, er gründete dieses auf die Syntax von Whiteheads und Russells Aussagenkalkül. Mallys deontisches Vokabular bestand aus den logischen Konstanten U und ∩, dem einwertigen Junktor ! und den zweiwertigen Junktoren f und ∞.

* Mally las !A als "A soll der Fall sein".
* Er las A f B als "A benötigt B" .
* Er las A ∞ B als "A und B benötigen einander."
* Er las U als "bedingungslose Verpflichtung".
* Er las ∩ als "bedingungsloses Verbot".

Mally definierte f, ∞ und ∩ wie folgt:

Def. f. A f B = A → !B
Def. ∞. A ∞ B = (A f B) & (B f A)
Def. ∩. ∩ = ¬U

Mally schlug fünf informelle Prinzipien vor:

(i) Falls A B benötigt und falls aus B C folgt, dann benötigt A C.
(ii) Falls A B benötigt und falls A C benötigt, dann benötigt A B und C.
(iii) A benötigt B falls und nur falls es verpflichtend ist, dass B aus A folgt.
(iv) Die bedingungslose Verpflichtung ist verpflichtend.
(v) Die bedingungslose Verpflichtung benötigt nicht ihre eigene Negation.

Er formalisierte diese Prinzipien als seine Axiome:

I. ((A f B) & (B → C)) → (A f C)
II. ((A f B) & (A f C)) → (A f (B & C))
III. (A f B) ↔ !(A → B)
IV. ∃U !U
V. ¬(U f ∩)

Aus diesen Axiomen deduzierte Mally 35 Theoreme, von denen er viele seltsam fand. Die Axiome III. und IV. vermengen Faktensätze und Normen und verstoßen somit gegen Humes Gesetz. Karl Menger zeigte, dass !A ↔ A ein Theorem ist, so dass die Einführung des Zeichens ! irrelevant ist, weil bei Mally A sein soll, wenn A der Fall ist,[13] was Mallys System diskreditierte.[14] Mally führte den Begriff "deontisch" im Deutschen ein.[15]

Von Wrights erste sinnvolle Deontische Logik

Das erste sinnvolle System der deontischen Logik wurde von G. H. von Wright vorgeschlagen[16][17]. Von Wright führte den Begriff deontic im Englischen ein. Seither haben viele Philosophen und Informatiker viele Systeme der deontischen Logik entwickelt. Trotzdem blieb die deontische Logik eines der umstrittensten Teilgebiete der Logik.[18]

G. H. von Wright gründete 1951 seine deontische Logik nicht auf die Syntax des Aussagenkalküls wie Mally, sondern auf die alethische Modallogik von Leibniz, die Mally nicht beachtet hatte. Doch 1964 kehrte er in A New System of Deontic Logic zur Syntax des Aussagenkalküls zurück, was er in Deontic Logic: A Personal View und A New System of Deontic Logic näher erläuterte.

Klassische deontische Logik

In von Wrights erstem System wurden Verpflichtbarkeit und Erlaubbarkeit als Handlungseigenschaften aufgefasst. Doch kurz darauf fand man heraus, dass man einer deontischen Logik von Aussagen eine einfache und elegante Kripke-Semantik geben konnte, und Wright schloss sich an. Die so spezifizierte deontische Logik wurde die "Klassische Deontische Logik", oft bezeichnet als SDL, KD oder einfach D. Sie wird axiomatisiert durch die folgende Ergänzung der Klassischen Aussagen-Logik:

O(A\rightarrow B)\rightarrow (OA\rightarrow OB)

OA\to \lnot O\lnot A

Die Axiome besagen:

Falls es sein soll, dass A B impliziert, dann soll B sein, falls A sein soll.
Falls A sein soll, dann ist es nicht verpflichtend, dass A nicht sei.

FA heißt, dass A verboten ist, und ist formal definiert als $O\lnot A$ oder $\lnot PA$ .

Es gibt zwei wichtige Erweiterungen von SDL: Die erste besteht in der Ergänzung eines alethischen modalen Operators $\Box$ , um Kants These, sollen impliziere können, auszudrücken:

OA\to \Diamond A.

wobei $\Diamond \equiv \lnot \Box \lnot$ . Meist gilt $\Box$ mindestens als KT-Operator, meist sogar als S5-Operator.

Die zweite wichtige Ergänzung besteht aus der Ergänzung durch einen Operator der konditionalen Verpflichtung O(A/B): "Es ist verpflichtend, dass A, falls B". Die Ergänzung ist motiviert durch folgenden Fall: Es gelte, dass die Hungernden versorgt werden sollten. Werden Hungernde versorgt, so folgt daraus, dass es Hungernde gibt. Durch die Grundprinzipien der SDL folgt, dass es Hungernde geben solle. Das Argument gilt in jeder Normalen Modallogik wegen des Basis-Axioms K der SDL und des Prinzips:

\vdash A\to B\Rightarrow \ \vdash OA\to OB.

Führt man einen intensionalen konditionalen Operator ein, kann man sagen: Die Hungernden sollen versorgt werden, aber nur wenn es tatsächlich Hungernde gibt, formal geschrieben O(A/B). Daraus kann man dann nicht mehr ableiten, dass es Hungernde geben soll.

Dyadische deontische Logik

Ein wichtiges Problem der deontischen Logik ist die korrekte Repräsentation konditionaler Verpflichtungen, z. B. Falls du rauchst (s), benutze einen Aschenbecher (a)! Es ist unklar, ob eine der folgenden Repräsentationen adäquat ist:

O(\mathrm {smoke} \rightarrow \mathrm {ashtray} )

\mathrm {smoke} \rightarrow O(\mathrm {ashtray} )

Bei der ersten Repräsentation ist es eine Leere Wahrheit, dass man bei der Übertretung eines Verbots irgendeine weitere Handlung ausführen muss, egal ob diese verpflichtend, erlaubt oder verboten ist[19].

Bei der zweiten Repräsentation ergibt sich das Mörder-Paradox: Aus (1) Falls du mordest, tue es sanft!, (2) Du mordest. und (3) Um sanft zu morden, musst du morden. ergibt sich: Du sollst morden!

Einige deontischen Logiker reagierten darauf mit der Entwicklung von dyadischen deontischen Logiken, die binäre deontische Operatoren beinhalten:

O(A\mid B)

heißt es ist verpflichtend, dass A, falls B

P(A\mid B)

heißt es ist erlaubt, dass A, falls B.

(Die Schreibweise folgt der für Bedingte Wahrscheinlichkeit.) Dyadische deontische Logik hat nicht das Problem der deontischen Logik mit einwertigen Operatoren, jedoch andere Probleme.

Andere Variationen

Viele andere Varianten der Deontischen Logik wurden entwickelt, z. B. nicht-monotone deontische Logiken, parakonsistente deontische Logiken und dynamische deontische Logik. Nach der Darstellung einzelner Systeme liefert Edgar Morscher im 15. Kapitel seines Buchs "Normenlogik" (2012) einen Rückblick auf die Geschichte der Normenlogik seit "Ernst Mallys Fehlstart".

Jørgensens Dilemma

Deontische Logik hat ein Problem – Jørgensens Dilemma. Normen sind nicht wahrheitsfähig, doch werden in der Logik Wahrheitswerte verwendet. Es gibt zwei mögliche Antworten:

Deontische Logik behandelt logische Aussagen über Normen, nicht Normen.
Alternative Wahrheitstheorien, z. B. Wahrheit als Allgemeingültigkeit oder als Erfolg wie in der Sprechakt-Theorie.
Erweiterung des Folgerungsbegriffs, so dass wahrheitserhaltendes Schließen als Sonderfall des logischen Schließens überhaupt angesehen wird. (Aber auch dann können aus Normsätzen keine Aussagesätze gefolgert werden; und aus Aussagesätzen keine Normsätze. Ein Argument für ein Sollen muss dann auf den Wahrheitsanspruch verzichten, oder seine Geltung ohne Anspruch auf Wahrheit behaupten. Das entspricht nicht dem normalen Gebrauch von Argumenten. Gibt man die Wahrheitsfunktionalität des logischen Schließens auf, dann wird Logik zur bloßen Formalisierungskunst.)

Siehe auch

Einzelnachweise

Jan C. Joerden: Deontische Logik., in: Eric Hilgendorf, Jan C. Joerden (Hg.): Handbuch Rechtsphilosophie. Stuttgart, Metzler 2017, ISBN 978-3-476-05309-1, S. 242
Hans-Joachim Koch, Helmut Rüßmann: Juristische Begründungslehre: eine Einführung in Grundprobleme der Rechtswissenschaft. München: Beck, 1982 (Schriftenreihe der Juristischen Schulung; H. 22), ISBN 3-406-03452-7, S. 45
Vgl. Hans-Joachim Koch, Helmut Rüßmann: Juristische Begründungslehre: eine Einführung in Grundprobleme der Rechtswissenschaft. München: Beck, 1982 (Schriftenreihe der Juristischen Schulung; H. 22), ISBN 3-406-03452-7, S. 45
So Jan C. Joerden: Deontische Logik. , in: Eric Hilgendorf, Jan C. Joerden (Hg.): Handbuch Rechtsphilosophie. Stuttgart, Metzler 2017, ISBN 978-3-476-05309-1, S. 242 (243)
Vgl. Hans-Joachim Koch, Helmut Rüßmann: Juristische Begründungslehre: eine Einführung in Grundprobleme der Rechtswissenschaft. München: Beck, 1982 (Schriftenreihe der Juristischen Schulung; H. 22), ISBN 3-406-03452-7, S. 45 (statt p F benutzend)
Röhl, Klaus F.; Hans Christian Röhl: Allgemeine Rechtslehre. 3. Auflage. C. Heymanns, Köln u. a. 2008, § 22 II, S. 192
Vgl. Strobach, Einführung in die Logik (2005), S. 117
Nach Herberger, Maximilian; Dieter Simon: Wissenschaftstheorie für Juristen. Metzner, Frankfurt a. M. 1980, S. 185
Siehe Jan C. Joerden: Deontische Logik. , in: Eric Hilgendorf, Jan C. Joerden (Hg.): Handbuch Rechtsphilosophie. Stuttgart, Metzler 2017, ISBN 978-3-476-05309-1, S. 242 (243)
Herberger, Maximilian; Dieter Simon: Wissenschaftstheorie für Juristen. Metzner, Frankfurt a. M. 1980, S. 184
Huisjes, C. H., 1981, "Norms and logic," Thesis, University of Groningen
Knuuttila, Simo, 1981, “The Emergence of Deontic Logic in the Fourteenth Century,” in New Studies in Deontic Logic, Ed. Hilpinen, Risto, pp. 225–248, University of Turku, Turku, Finland: D. Reidel Publishing Company.
Menger, Karl, 1939, "A logic of the doubtful: On optative and imperative logic," in Reports of a Mathematical Colloquium, 2nd series, 2nd issue, pp. 53–64, Notre Dame, Indiana: Indiana University Press.
Mally's Deontic Logic von Gert Lokhorst bei der Stanford Encyclopedia of Philosophy
Mally, Deontik, 1926
G. H. von Wright, Deontic Logic in: Mind, 1951
Albert J.J. Anglberger, Eine Mögliche-Welten-Semantik für G. H. von Wrights ersten Kalkül der deontischen Logik in: Conceptus-Zeitschrift für Philosophie, Nr. 89–90, 2004
Albert J.J. Anglberger, Non-Kognitivismus und Normenlogik: Betrachtungen zu einer mehrwertigen Mögliche-Welten-Semantik, in: Kreuzbauer, G./Gratzl, N./Hiebl, E. (Eds.): Persuasion und Wissenschaft: Aktuelle Fragestellungen von Rhetorik und Argumentationstheorie 2006, Wien, LIT-Verlag, 2007
Von Wright 1956, zitiert in Aqvist 1994

Literatur

Jan C. Joerden: Deontische Logik, in: Eric Hilgendorf, Jan C. Joerden (Hg.): Handbuch Rechtsphilosophie Stuttgart, Metzler 2017, ISBN 978-3-476-05309-1, S. 242–245
Lennart Åqvist, 1994, "Deontic Logic" in D. Gabbay and F. Guenthner, ed., Handbook of Philosophical Logic: Volume II Extensions of Classical Logic. Kluwer.
Hilpinen, Risto, 2001, "Deontic Logic," in Goble, Lou, ed., The Blackwell Guide to Philosophical Logic. Blackwell.
G. H. von Wright, 1951. "Deontic logic," Mind 60: 1–15.
Franz von Kutschera: Einführung in die Logik der Normen, Werte und Entscheidungen. Freiburg i. Br./ München, Alber, 1973.
Hans Lenk (Hrsg.): Normenlogik. Grundprobleme der deontischen Logik. Pullach bei München, Verlag Dokumentation, 1974.

Weblinks

McNamara, Deontic Logic, Stanford Encyclopedia of Philosophy, 2006.
KED (PDF-Datei; 91 kB) -- Hyperlink ungültig!

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Jan_C_2017-1] Jan C. Joerden: Deontische Logik., in: Eric Hilgendorf, Jan C. Joerden (Hg.): Handbuch Rechtsphilosophie. Stuttgart, Metzler 2017, ISBN 978-3-476-05309-1, S. 242

[2] Hans-Joachim Koch, Helmut Rüßmann: Juristische Begründungslehre: eine Einführung in Grundprobleme der Rechtswissenschaft. München: Beck, 1982 (Schriftenreihe der Juristischen Schulung; H. 22), ISBN 3-406-03452-7, S. 45

[3] Vgl. Hans-Joachim Koch, Helmut Rüßmann: Juristische Begründungslehre: eine Einführung in Grundprobleme der Rechtswissenschaft. München: Beck, 1982 (Schriftenreihe der Juristischen Schulung; H. 22), ISBN 3-406-03452-7, S. 45

[ReferenceA-4] So Jan C. Joerden: Deontische Logik. , in: Eric Hilgendorf, Jan C. Joerden (Hg.): Handbuch Rechtsphilosophie. Stuttgart, Metzler 2017, ISBN 978-3-476-05309-1, S. 242 (243)

[5] Vgl. Hans-Joachim Koch, Helmut Rüßmann: Juristische Begründungslehre: eine Einführung in Grundprobleme der Rechtswissenschaft. München: Beck, 1982 (Schriftenreihe der Juristischen Schulung; H. 22), ISBN 3-406-03452-7, S. 45 (statt p F benutzend)

[6] Röhl, Klaus F.; Hans Christian Röhl: Allgemeine Rechtslehre. 3. Auflage. C. Heymanns, Köln u. a. 2008, § 22 II, S. 192

[7] Vgl. Strobach, Einführung in die Logik (2005), S. 117

[8] Nach Herberger, Maximilian; Dieter Simon: Wissenschaftstheorie für Juristen. Metzner, Frankfurt a. M. 1980, S. 185

[9] Siehe Jan C. Joerden: Deontische Logik. , in: Eric Hilgendorf, Jan C. Joerden (Hg.): Handbuch Rechtsphilosophie. Stuttgart, Metzler 2017, ISBN 978-3-476-05309-1, S. 242 (243)

[Herberger,_Maximilian_1980-10] Herberger, Maximilian; Dieter Simon: Wissenschaftstheorie für Juristen. Metzner, Frankfurt a. M. 1980, S. 184

[Greece-11] Huisjes, C. H., 1981, "Norms and logic," Thesis, University of Groningen

[ones-12] Knuuttila, Simo, 1981, “The Emergence of Deontic Logic in the Fourteenth Century,” in New Studies in Deontic Logic, Ed. Hilpinen, Risto, pp. 225–248, University of Turku, Turku, Finland: D. Reidel Publishing Company.

[A-13] Menger, Karl, 1939, "A logic of the doubtful: On optative and imperative logic," in Reports of a Mathematical Colloquium, 2nd series, 2nd issue, pp. 53–64, Notre Dame, Indiana: Indiana University Press.

[14] Mally's Deontic Logic von Gert Lokhorst bei der Stanford Encyclopedia of Philosophy

[15] Mally, Deontik, 1926

[16] G. H. von Wright, Deontic Logic in: Mind, 1951

[17] Albert J.J. Anglberger, Eine Mögliche-Welten-Semantik für G. H. von Wrights ersten Kalkül der deontischen Logik in: Conceptus-Zeitschrift für Philosophie, Nr. 89–90, 2004

[18] Albert J.J. Anglberger, Non-Kognitivismus und Normenlogik: Betrachtungen zu einer mehrwertigen Mögliche-Welten-Semantik, in: Kreuzbauer, G./Gratzl, N./Hiebl, E. (Eds.): Persuasion und Wissenschaft: Aktuelle Fragestellungen von Rhetorik und Argumentationstheorie 2006, Wien, LIT-Verlag, 2007

[19] Von Wright 1956, zitiert in Aqvist 1994