Debye-Scherrer-Verfahren
Das Debye-Scherrer-Verfahren dient der Untersuchung und Identifikation pulverförmiger kristalliner Substanzen durch Röntgenbeugung. Das Verfahren wurde 1916/17 von den Physikern Peter Debye und Paul Scherrer mit einer Ionenröhre von Heinrich Rausch von Traubenberg und unabhängig davon durch Alfred Hull entwickelt.[1][2]
Die Untersuchung pulverförmiger Proben stellte eine deutliche experimentelle Vereinfachung im Vergleich zum 1912 entwickelten Laue-Verfahren dar, welches die Strukturbestimmung mittels Röntgenbeugung nur an Einkristallen erlaubte.
Aufbau

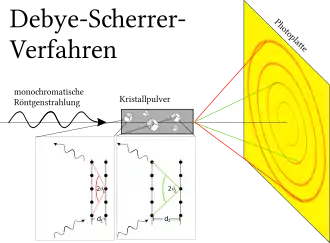
Um eine Probe aus pulverisiertem kristallinem Material mit dieser Methode zu untersuchen, wird in einem bestimmten Abstand r ein fotografischer Film in einem (fast vollständigen) Kreis um die Probe positioniert und bildet so die Filmkammer. Durch eine Lücke wird die Probe mit einem feinen monochromatischen Röntgenstrahlbündel beschossen.
Zur Vereinfachung der quantitativen Auswertung wird der Radius der Filmkammer oft zu r = 360 mm / 2π = 57,3 mm gewählt, so dass der Umfang der Filmkammer genau 360 mm entspricht.[3] Folglich entspricht auf dem ausgerollten (entwickelten) Film 1 mm genau einem Winkel von 1°; bei einem Radius der Kammer von 57,3 mm / 2 = 28,65 mm entspricht 1 mm auf dem Film 2°.
Auch wenn diese Vorgehensweise noch oft in Ausbildungspraktika verwendet wird, basieren heutige Instrumente oft auf einer digitalen Erfassung, so dass die Kammerkonstruktion mit fotografischem Film inzwischen nebensächlich geworden ist.
Beobachtung
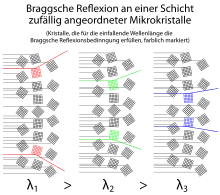
Treffen die monochromatischen Röntgenstrahlen ein kristallines Teilchen der Probe gerade so, dass die Bragg-Gleichung erfüllt ist, so werden sie optimal gebeugt. Das heißt, sie verstärken sich gegenseitig (positive Interferenz) und erzeugen mit den anderen optimal gebeugten Strahlen derselben Gitterebene einen Kegel. Dies wird in der nebenstehenden Abbildung z. B. für die Wellenlänge λ1 für zwei Strahlen (rot) dargestellt, welche an derselben Gitterebene von verschieden ausgerichteten Kristalliten gebeugt werden. Nimmt man weitere Strahlen und die Beugung an dieser Gitterebene an allen weiteren möglichen Ausrichtungen der Kristallite hinzu, so entsteht eine kegelförmige Strahlungsverteilung. Das Abbild dieses Kegels ist als kreisförmiges Diffraktogramm (auch Beugungsring genannt) auf dem Film zu sehen.
Auswertung
Nach Ausmessen des Durchmessers eines Beugungsrings auf dem Film ergibt sich der Beugungswinkel (Reflexions-, Glanz- oder Bragg-Winkel). Dies führt man für alle sichtbaren Beugungsringe durch, wobei die einzelnen Ringe von innen nach außen durchnummeriert werden (0. Ordnung, 1. Ordnung usw.). Mit Hilfe der Bragg-Gleichung lässt sich der Netzebenenabstand der jeweils reflektierenden Netzebenenschar berechnen. Unter Einbeziehung der Millerschen Indizes lassen sich daraus für das vorliegende Kristallsystem die jeweiligen Gitterkonstanten ermitteln.
Umgekehrtes Debye-Scherrer-Verfahren
Kennt man die Gitterabstände des pulverisierten Materials, so kann das Debye-Scherrer-Verfahren umgekehrt auch dazu verwendet werden, die Wellenlängen unbekannter Röntgenstrahlen zu bestimmen: Ändert sich die Wellenlänge der einfallenden Röntgenstrahlen, so entstehen, wie nebenstehende Abbildung für die Wellenlängen λ1, λ2 und λ3 illustrieren soll, Kegel unterschiedlichen Öffnungswinkels. Ist die Zuordnung dieser Beugungsringe also für eine Wellenlänge bekannt, so können aus der Größe der Beugungsringe bei anderen Wellenlängen mittels der Bragg-Gleichung auch die Werte der anderen Wellenlängen bestimmt werden.
Literatur
- Peter Debye, Paul Scherrer: Interferenzen an regellos orientierten Teilchen im Röntgenlicht. In: Nachr. Ges. Wiss. Göttingen (1916). 4. Dezember 1915, S. 1–26, abgerufen am 3. September 2019.
- Peter Kasten: Strukturaufklärung von Kristallpulver - Hundert Jahre Debye-Scherrer-Verfahren. In: Physik in unserer Zeit. Band 46, Nr. 4, 2015, S. 174–179, doi:10.1002/piuz.201401405.
- Peter Kasten: The search for electron rings inside atoms led to the Debye-Scherrer method. In: Annalen der Physik. Band 528, Nr. 11, 2016, S. 761–764, doi:10.1002/andp.201600306.
Einzelnachweise
- Martin Etter, Robert E. Dinnebier: A Century of Powder Diffraction: a Brief History. In: Zeitschrift für anorganische und allgemeine Chemie. Band 640, Nr. 15, 2014, S. 3015–3028, doi:10.1002/zaac.201400526.
- André Authier: Early Days of X-ray Crystallography. 1. Auflage. Oxford University Press, Oxford 2013, ISBN 978-0-19-965984-5, 8.5, S. 190–195.
- Debye-Scherrer-Kamera 806/807. In: Online-Produkt-Katalog. Fa. HUBER Diffraktionstechnik GmbH & Co. KG, abgerufen am 22. Juni 2016.