Bistabilität

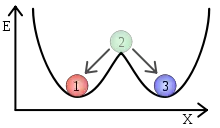
Bistabilität (von lat. bi = zwei und lat. stabilis = standhaft, stabil) ist die Eigenschaft einiger Systeme, zwei mögliche stabile Zustände einnehmen zu können, aber nur durch einen äußeren Impuls vom einen in den anderen Zustand zu wechseln. Diese Systeme heißen dann bistabile Systeme. Wichtig dabei ist, dass diese Zustände bei ein und denselben Parameterwerten angenommen werden können, im Gegensatz etwa zur Ultrasensitivität, wo ein scharfer Übergang durch Änderung von Parameterwerten hervorgerufen wird. Meist handelt es sich bei den Zuständen um stationäre Zustände im Sinne von Fließgleichgewichten.

Die zwei Zustände 1 und 3 sind stabil, der Übergangszustand 2 ist labil.

Mathematische Beschreibung

Bistabiles Verhalten wird meist durch eine positive Rückkopplung hervorgebracht. Jeder der Zustände stabilisiert sich dadurch selbst.

Kann das Verhalten eines Systems durch Differentialgleichungen beschrieben werden, so kann Bistabilität schon in eindimensionalen Systemen auftreten, d. h., es genügt eine unabhängige Variable, während für Oszillationen zweidimensionale Systeme nötig sind. Die Differentialgleichungen müssen aber nichtlinear sein. In linearen Systemen sind nämlich nur drei Fälle möglich: Es gibt genau einen stationären Zustand, gar keinen stationären Zustand oder ein Kontinuum solcher Zustände. Bei Bistabilität müssen aber zwei isolierte Zustände auftreten.

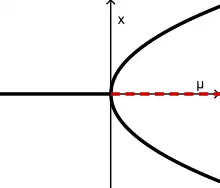
Die Gabelbifurkation zeigt von links nach rechts den Übergang von einem stabilen zu einem bistabilen System. Dicke schwarze Kurven: stabile Zustände; rot gestrichelt: instabiler (labiler) Zustand.

Der Übergang zwischen einem stabilen und einem bistabilen System kann mit Hilfe des rechts dargestellten Gabelbifurkationsdiagrammen dargestellt werden.

Beispiele aus verschiedenen Fachgebieten

Ein Beispiel aus dem Alltag ist ein Lichtschalter mit Sprungkontakt: Solange er nicht angefasst wird, verbleibt er in einer Position (an oder aus). Nach dem Loslassen springt er entweder zurück in die alte Position (nicht fest genug gedrückt) oder in die neue Position (fest genug gedrückt für eine normale Betätigung).

Weitere Beispiele aus dem Bereich der Technik sind das Flipflop in der Elektronik oder bistabile Federn in der Mechanik. Auch komplexe Systeme, wie beispielsweise demokratische Staaten mit zwei großen Parteien, die abwechselnd die Mehrheit im Parlament erringen, können zumindest zeitweise bistabil sein.

Weblinks

Wiktionary: bistabil – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Referenzen

W. Ebeling, R. Feistel, Physik der Selbstorganisation und Evolution. Akademie-Verlag, Berlin 1982

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.