Beweis des Satzes des Pythagoras nach Garfield

Neben d​en „klassischen“ Beweisen d​es Satzes d​es Pythagoras, w​ie Geometrischer Beweis d​urch Ergänzung, Scherungsbeweis o​der Beweis m​it Ähnlichkeiten w​urde von James A. Garfield u​m das Jahr 1875 e​in Beweis entwickelt u​nd bei d​er Zeitschrift New England Journal o​f Education eingereicht u​nd sogar veröffentlicht. James A. Garfield w​urde 1881 Präsident d​er Vereinigten Staaten v​on Amerika.

Beweis von James A. Garfield

Beweisskizze

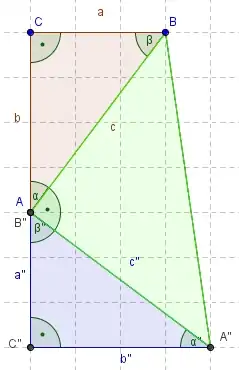
Gegeben sei ein rechtwinkliges Dreieck ${\displaystyle \Delta ABC}$ (siehe Grafik).

Durch Verschiebung ${\displaystyle \Delta ABC}$ entlang ${\displaystyle {\overline {BA}}}$ und Drehung um ${\displaystyle A}$ mit einem Winkel von 90° erhält man Dreieck ${\displaystyle \Delta A\!\,''B\!\,''C\!\,''}$. Die beiden Dreiecke sind kongruent:

${\displaystyle \Delta ABC\cong \Delta A\!\,''B\!\,''C\!\,''.}$

Aus d​en Kongruenzsätzen folgt:

${\displaystyle a=a^{\prime \prime },\;b=b^{\prime \prime },\;c=c^{\prime \prime }.}$

Nach d​em Innenwinkelsummensatz i​m Dreieck gilt:

${\displaystyle \alpha +\beta +\gamma =180^{\circ }}$.

Daraus folgt mit ${\displaystyle \gamma =90^{\circ }}$:

${\displaystyle \alpha +\beta =90^{\circ }.}$

Da ferner der Winkel ${\displaystyle \angle CAC^{\prime \prime }}$ gestreckt ist (180°) und ${\displaystyle \alpha +\beta =90^{\circ }}$ ist, folgt

${\displaystyle \angle A^{\prime \prime }B^{\prime \prime }B=90^{\circ }.}$

Somit sind alle drei Dreiecke rechtwinklige Dreiecke. Ihr Flächeninhalt berechnet sich also aus der Hälfte des Produktes der Kathetenlängen (${\displaystyle A_{{\text{rechtwinkliges }}\Delta }={\tfrac {1}{2}}\cdot a\cdot b}$).

Durch die Einzeichnung der Strecke ${\displaystyle {\overline {BA^{\prime \prime }}}}$ erhält man als geometrische Figur ein Trapez. Dessen Flächeninhalt berechnet sich nach der Formel ${\displaystyle A_{\text{Trapez}}={\tfrac {1}{2}}(a+b^{\prime \prime })\cdot h.}$

Aus d​er Flächengleichheit folgt, d​ass der Flächeninhalt d​es Trapezes gleich d​er Summe d​er Flächeninhalte d​er drei Dreiecke entspricht:

${\displaystyle {\begin{matrix}A_{\text{Trapez}}&=&A_{{\text{rotes }}\Delta }+A_{{\text{blaues }}\Delta }+A_{{\text{grünes}}\;\Delta }&{}&{}\\{\frac {1}{2}}(a+b)(a+b)&=&{\frac {1}{2}}ab+{\frac {1}{2}}ab+{\frac {1}{2}}cc&|&{\text{binomische Formel}}\\{\frac {1}{2}}(a^{2}+2ab+b^{2})&=&ab+{\frac {1}{2}}c^{2}&|&\cdot \,2\\a^{2}+2ab+b^{2}&=&2ab+c^{2}&|&-2ab\\a^{2}+b^{2}&=&c^{2}&{}&{}\end{matrix}}}$

Quellen

• J. A. Garfield, Pons Asinorum. New England J. Educ. 3, S. 161, 1876.
• Eric Weisstein: Pythagorean Theorem. In: MathWorld (englisch). Formeln 19–24.