Betriebsoptimum
In der Mikroökonomie wird das Betriebsoptimum als das Minimum der durchschnittlichen totalen Kosten (Stückkosten) bezeichnet. Gelegentlich wird auch die Lage des Minimums, also die zugehörige Produktionsmenge, oder der entsprechende Punkt als Betriebsoptimum bezeichnet.[1] Der dazugehörige Stückpreis wird "langfristige Preisuntergrenze" genannt, da der Produktpreis diese Grenze aus Sicht der Vollkostenrechnung nicht unterschreiten darf, damit keine Verluste entstehen. Bei dauerhaften Verlusten kann keine (privatwirtschaftliche) Produktion erfolgen. Aus Sicht der Teilkostenrechnung müsste vorher überprüft werden, ob die unterschrittene langfristige Preisuntergrenze noch oberhalb der kurzfristigen Preisuntergrenze liegt und somit noch ein positiver Deckungsbeitrag erzielt wird.
Bei einem Preis in Höhe des Betriebsoptimums befinden sich die Unternehmen in einer Null-Gewinn-Situation. Das Betriebsoptimum entspricht in diesem Fall gleichzeitig der Gewinnschwelle, der Gewinngrenze und dem Gewinnmaximum (= 0!). Die Konsumenten können das Produkt zum (auf lange Sicht) günstigsten Preis erwerben und der bewertete Ressourcenverbrauch je Produkteinheit ist minimal. Den Preis auf das Betriebsoptimum zu setzen ist für einen Betrieb vor allem dann sinnvoll, wenn er sich in einem Verdrängungswettbewerb befindet oder das Produkt ohne Gewinnabsicht produziert.
Berechnet wird das Betriebsoptimum, indem man die erste Ableitung der Stückkostenfunktion = 0 setzt. Setzt man anschließend den auf diese Weise ermittelten x-Wert in die Stückkostenfunktion ein, so erhält man die langfristige Preisuntergrenze.
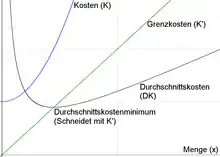
Das gleiche Ergebnis ergibt sich, wenn man den Schnittpunkt der Grenzkostenkurve K'(x) und der Stückkostenkurve k(x) berechnet, indem man beide Funktionen gleich setzt und die Lösungsmenge bestimmt.
Siehe auch
Einzelnachweise
- Corsten: Produktionswirtschaft 6. Auflage, S. 96