Bedingungsloser Zug
Ein bedingungsloser Zug ist ein Begriff aus der Spieltheorie und zählt als Ausprägung zu den strategischen Zügen (Strategischer Zug). Ein Spieler, der einen bedingungslosen Zug wählt, agiert vor seinen Gegenspielern und legt damit seine eigene Handlung fest. Die Entscheidung, die ein Spieler trifft wird in diesem Kontext als Zug bezeichnet. Bedingungslos bedeutet in diesem Zusammenhang uneingeschränkt und unabhängig von den Handlungen anderer.
Entstehung eines bedingungslosen Zuges
Der bedingungslose Zug ist eine Antwortregel, bei der man den ersten Zug macht und damit die eigene Handlung festlegt.[1] Es muss sich also um ein Spiel handeln, bei dem die Züge aus strategischen Gründen bewusst nacheinander stattfinden. Ist dies der Fall, spricht man von einem Spiel mit sequenziellen Zügen. Zur besseren Veranschaulichung sollen im Folgenden die Beweggründe für die Wahl eines bedingungslosen Zuges dargestellt werden.
Erläuterung
Ein Ausgangspunkt für die Entstehung eines bedingungslosen Zuges ist ein Spiel mit simultanen Zügen. In einem solchen Spiel müssen die Spieler eine Entscheidung treffen oder einen Zug wählen, ohne zu wissen, wie sich der jeweils andere entscheidet. Ein simultanes Spiel findet also unter unvollkommener Information statt. Jedoch kann ein Spieler in einem Spiel eine dominante Strategie haben. Das ist dann gegeben, wenn es einen Zug gibt, bei dem die eigenen Ergebnisse, egal wie sich die Gegenpartei entscheidet, in jedem Fall besser sind als bei der Wahl des anderen möglichen Zuges. Erkennt der Gegenspieler diese dominante Strategie, kann er sich mit seiner Antwort auf die Strategie seines Gegners einstellen. Das wiederum kann auf der Gegenseite trotz dominanter Strategie zu einem Nachteil führen.
Es ist besonders dann vorteilhaft für eine Partei, die Initiative zu ergreifen, wenn sie in ihrem Verhalten berechenbar ist und dies von den anderen Parteien ausgenutzt werden kann. Ergreift die Partei in einer solchen Situation die Initiative, kann sie möglicherweise den Konfliktverlauf zu ihren Gunsten ändern.[2]
Die eigene Situation kann mit Hilfe eines strategischen Zuges in Form eines bedingungslosen Zuges verbessert werden. Es tritt dabei der Effekt ein, dass aus einem simultanen Spiel ein sequenzielles Spiel wird, da der Spieler seine Entscheidung bewusst vorab bekannt gibt. Die Züge werden somit nicht mehr gleichzeitig, sondern nacheinander ausgeführt.
Beispiel
Im Jahr 2006 übernimmt der Sportartikelhersteller adidas den US-Konkurrenten Reebok. Adidas will damit seinen Marktanteil stärken, auf dem Nike die Führerschaft innehat. Die bisherigen „Hauptmärkte“ der beiden Konkurrenten, USA und Europa, stagnieren. Beide Kontrahenten versuchen zunehmend in die Märkte von Entwicklungsländern wie beispielsweise Indien oder China einzutreten und die eigene Position zu stärken.
Stellen wir uns als Beispiel folgendes Szenario vor: Beide Hersteller versuchen mit hohen Werbeausgaben auf den Märkten zu punkten. Es ist zu entscheiden, ob die beiden Sportartikelhersteller mit einem großen oder kleinen Werbebudget in die Märkte eindringen. Das Ergebnis, was beide erzielen können, ist davon abhängig, wie viel der jeweils andere in Werbung investiert. Da sich beide einen Markt teilen, können Verschiebungen des Marktanteils mittels Werbung beeinflusst werden. Nehmen wir weiter an, dass geringere Werbeausgaben adidas entgegenkommen würden. Nike hingegen kann auch ein großes Werbebudget verkraften.
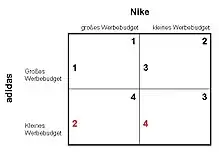
Aus nebenstehender Tabelle ist zu erkennen, dass die Ergebnisse (4 → bestes Ergebnis bis 1 → schlechtestes Ergebnis) für adidas (Ergebnisse jeweils links unten im Quadrat dargestellt) im Falle der Wahl eines kleinen Werbebudgets immer besser sind, als bei der Wahl eines großen Werbebudget. Für adidas ist ein kleines Budget die dominante Strategie (rot gekennzeichnete Ergebnisse). Erkennt Nike (Ergebnisse rechts oben im Quadrat) die dominate Strategie von adidas, so wird Nike ein großes Werbebudget wählen. Für adidas bedeutet das ein Ergebnis von lediglich 2, welches trotz dominanter Strategie ein schlechteres Ergebnis ist.
Wie adidas sein Ergebnis verbessern kann, wird im nachfolgenden Gliederungspunkt beschrieben.
Erläuterung
Der bedingungslose Zug kann ein simultanes Spiel in ein sequenzielles Spiel „umwandeln“. Das geschieht, indem ein Spieler eine einseitige bedingungslose Ankündigung macht. Mit anderen Worten, ein Spieler wird aktiv und nimmt seine Entscheidung vorweg. Somit nimmt er direkt Einfluss auf den Verlauf des Spiels, weil er somit die Entscheidung der Gegenspieler beeinflusst.
Die Entscheidung, welcher bedingungslose Zug gewählt werden soll erfolgt, indem man vorausblickt und ausgehend von den möglichen Ergebnissen Rückschlüsse zieht, welches Verhalten am günstigsten ist.[3]
Der Vorteil, der aus einem bedingungslosen Zug entstehen kann, wird auch als First-Mover´s-Advantage bezeichnet. Mit anderen Worten, der Spieler, der den ersten Zug machen kann, ist im Vorteil.
Beispiel
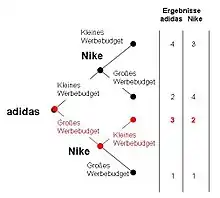
Betrachtet man nochmals obiges Beispiel, dann kann adidas mit einem bedingungslosen Zug seine Situation verbessern. Adidas sollte folglich den ersten Zug spielen und ein großes Werbebudget ankündigen. Damit ist es für Nike günstiger ein kleines Werbebudget aufzulegen und adidas erzielt ein, um ein Punkt besseres Ergebnis. Die Ergebnisse können aus der nebenstehenden Graphik entnommen werden.
Erfolgsfaktoren
Der Erfolg eines bedingungslosen Zuges ist von mehreren Faktoren abhängig, die im Folgenden kurz erläutert werden. Diese Faktoren bestimmen, ob die Entscheidung des Gegenspielers mit einem bedingungslosen Zuges beeinflussbar ist.
Selbstverpflichtung
Der Spieler, der einen bedingungslosen Zug wählt, muss sich selbst verpflichten, nicht die Entscheidung seiner dominanten Strategie zu wählen. Er muss sich mit seiner Entscheidung festlegen.
Glaubwürdigkeit
Weiterhin spielt die Glaubwürdigkeit des bedingungslosen Zuges eine wichtige Rolle. Der Gegenspieler darf nicht mit dem Gedanken spielen, dass man doch eine andere Entscheidung trifft. Man muss dem Gegner also überzeugend vermitteln, dass man bei seiner bedingungslosen Ankündigung bleibt. Andernfalls hat der Gegner keinen Grund so zu reagieren, wie man es von ihm erwartet.
Selbstbindung
Der bedingungslose Zug sollte bekräftigt werden, indem man die eigene Entscheidung irreversibel macht. Somit ist eine andere Entscheidung nicht mehr möglich und dem Gegner wird durch die Selbstbindung verdeutlicht, dass keine andere Handlungsalternative mehr möglich ist.
Erster Zug
Die Entscheidung des Gegenspielers darf zeitlich nicht vor der eigenen Entscheidung stattfinden. Ein nachträglicher bedingungsloser Zug hat keine Wirkung mehr.
Bekanntheit
Der Gegenspieler muss die Entscheidung kennen. Kennt er sie nicht, kann sie auch keinen Einfluss auf seine Handlungen haben.
Ergebnis
Die Entscheidungen in einem simultanen Spiel und einem sequenziellen Spiel müssen nicht übereinstimmen. Ein bedingungsloser Zug muss nicht zwingend zu einem Erfolg führen oder die Entscheidungen in einem Spiel beeinflussen. Die Wirkung ist von einer Reihe von Faktoren abhängig. Weiterhin sind Spielkombinationen denkbar, in denen ein bedingungsloser Zug keinen Einfluss auf den Spielverlauf hat. In solchen Situationen kann der strategische Zug durch Versprechen, Beteuerung, Warnung oder Drohung positiv beeinflusst werden. Des Weiteren kann die Strategie darin bestehen, den Gegner einen bedingungslosen Zug durchführen zu lassen und darauf zu reagieren.
Belege
- Avinash K. Dixit, Barry J. Nalebuff (Hrsg.): Spieltheorie für Einsteiger. 1997, S. 122.
- Peter-Jürgen Jost: Strategisches Konfliktmanagement in Organisationen. 1999, S. 223.
- Avinash K. Dixit, Barry J. Nalebuff (Hrsg.): Spieltheorie für Einsteiger. 1997, S. 120.
Literatur
- Avinash K. Dixit, Barry J. Nalebuff (Hrsg.): Spieltheorie für Einsteiger – Strategisches Know-how für Gewinner. Schäffer-Poeschel Verlag, Stuttgart 1997, ISBN 3-7910-1239-8 (Basisliteratur zu diesem Artikel)
- Avinash K. Dixit, Susan Skeath (Hrsg.): Games of Strategy. 2. Auflage. W. W. Norton & Company, 2004, ISBN 0-393-92499-8.
- Peter-Jürgen Jost: Strategisches Konfliktmanagement in Organisationen: Eine spieltheoretische Einführung. Gabler Verlag, 1999, ISBN 3-409-22256-1.
- Eric Rasmusen: Games and information: an introduction to game theory. Blackwell Publishing, Oxford 2007, ISBN 978-1-4051-3666-2.
- Thomas Riechmann: Spieltheorie. 2. Auflage. Verlag Vahlen, München 2008, ISBN 978-3-8006-3505-4.