Asthenosphäre
Die Asthenosphäre (altgriechisch ἀσθενής asthenés, deutsch ‚kraftlos‘, ‚schwach‘),[1] in der Geophysik auch Low Velocity Zone genannt, ist die zweitäußerste Schicht des rheologischen Modells des Erdinneren und schließt sich unterhalb der Lithosphäre an. Sie beginnt, je nach Mächtigkeit der Lithosphäre, in einer Tiefe von 60 bis 210 km und reicht hinunter bis in eine Tiefe von 300 bis 410 km. Ihr mechanisches Verhalten kann vereinfachend als duktil (plastisch verformbar) beschrieben werden. Auf der Asthenosphäre bewegen sich die vergleichsweise starren und weniger dichten Lithosphärenplatten.
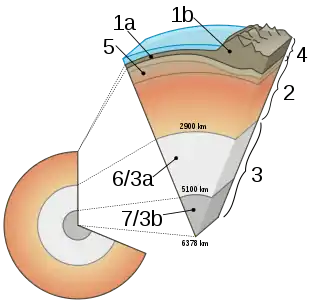
Schichten nach chemischer Zusammensetzung:
1 Erdkruste, 2 Erdmantel, 3 Erdkern
(3a äußerer Erdkern, 3b innerer Erdkern)
Schichten nach mechanischen Eigenschaften:
4 Lithosphäre, 5 Asthenosphäre
6 äußerer Erdkern, 7 innerer Erdkern
Eigenschaften
Von der mineralischen Zusammensetzung her unterscheidet sich die Asthenosphäre nicht vom Gestein des oberen Erdmantels. Hauptbestandteile sind Olivin, Orthopyroxen, Spinell und Granat. Die mittlere Dichte beträgt 3300 kg/m³.
Der weitaus bedeutendere Unterschied zwischen der Asthenosphäre und den ihr auf- und unterlagernden Schichten besteht in ihren mechanischen Eigenschaften. So breiten sich seismische Wellen innerhalb der Asthenosphäre langsamer aus als in den unmittelbar benachbarten Schichten. Darauf verweist die englische Bezeichnung low velocity zone (LVZ). Je nach Definition ist die LVZ gleichbedeutend mit der Asthenosphäre, oder sie umfasst nur die oberen 100 km. Die mittlere Geschwindigkeit der P-Wellen fällt von 8,3 km/s unterhalb der Mohorovičić-Diskontinuität auf weniger als 8 km/s unterhalb der Lithosphäre-Asthenosphäre-Grenze (LAB) ab, um mit zunehmender Tiefe wieder zuzunehmen. Bis zum Erdkern steigt sie letztlich auf 13,6 km/s an. Scherwellen (S-Wellen) werden vom teilaufgeschmolzenen Gestein gedämpft.
Die dynamische Viskosität der Asthenosphäre lässt sich aus postglazialen Hebungen abschätzen. Sie liegt zwischen 1020 Pascalsekunden (Pa·s) unter Mittelozeanischen Rücken, Subduktionszonen und sonstigen seismisch sehr aktiven Regionen und 1024 Pa·s unter Kratonen.[2][3] Die Viskosität der Kruste ist mit mehr als 1025 Pa·s deutlich größer. Zum Vergleich: die Viskosität von Glas beträgt ca. 1017 Pa·s.
Die Fließfähigkeit der Asthenosphäre hängt von der Solidustemperatur, dem Gehalt an Gesteinswasser und dem geothermischen Gradienten ab. Die Solidustemperatur ist die vom Druck (und damit der Tiefe) abhängige Temperatur, bei der das Gestein zu schmelzen beginnt. Ist in der Asthenosphäre diese Temperatur überschritten, kann das Gestein zu 1–5 % partiell aufschmelzen (Magma). Die Bildung der Schmelze wird vor allem durch die Instabilität wasserhaltiger Silikat-Minerale in dieser Tiefe hervorgerufen. Wasser verursacht bereits in kleinen Mengen eine deutliche Senkung der Solidustemperatur. Es stammt aus dem Orthopyroxen und in geringem Umfang aus dem Olivin. In Gegenwart von Aluminium kann Orthopyroxen größere Mengen Wasser binden, die es bei zunehmendem Druck in einer Tiefe von 100 bis 150 km wieder abgibt. Die Viskosität hängt außerdem noch vom geothermischen Gradienten und damit auch vom Alter der darüberliegenden Platte ab. Je älter eine Platte, umso niedriger der Gradient, eine höhere Viskosität ist die Folge.[2]
Asthenosphäre des Mondes
Beim Erdmond beginnt die plastische Asthenosphäre in 800–1000 km Tiefe, also etwa beim halben Mondradius. Hier haben auch die meisten Mondbeben ihren Ursprung.
Diese Tiefe ergibt sich aus dem gemessenen Wärmefluss der Apollo-Missionen und aus der starken Dämpfung der seismischen Scherwellen. In welcher Tiefe hingegen der Mondkern beginnt, ist noch ungewiss.
Einzelnachweise
- Vgl. Duden online: Asthenie
- Attreyee Ghosh, William E. Holt: Plate Motions and Stresses from Global Dynamic Models. In: Science. 335, Nr. 6070, 2012, S. 838–843. doi:10.1126/science.1214209.
- G. Kaufmann, K. Lambeck: Glacial isostatic adjustment and the radial viscosity profile from inverse modeling. In: Journal of Geophysical Research. 107, Nr. B11, 2002, S. 2280. bibcode:2002JGRB..107.2280K. doi:10.1029/2001JB000941. PDF