Abtastratenkonvertierung
Die Abtastratenkonvertierung (englisch Sample rate conversion oder Resampling) beschreibt im Rahmen der digitalen Signalverarbeitung die Umsetzung eines Digitalsignals zwischen zwei verschiedenen Abtastraten unter möglichst vollständiger Beibehaltung der Signalinformation. Im Bereich der digitalen Bildbearbeitung von Rastergrafiken wird dieser Vorgang auch als Skalierung bezeichnet.
Allgemeines
Erfolgt die Umsetzung von einer hohen Abtastrate auf eine niedrigere Abtastrate wird dies auch als Downsampling (Dezimation) bezeichnet, die umgekehrte Umsetzung von einer niedrigen Abtastrate auf eine hohe Abtastrate wird als Upsampling (Interpolation) bezeichnet. Um die Information im Signal möglichst wenig zu verfälschen, muss bei der Abtastratenkonvertierung das Nyquist-Shannon-Abtasttheorem beachtet werden. Dies bedeutet insbesondere, dass Frequenzanteile im Signal nicht über der Nyquist-Frequenz der niedrigeren Abtastrate liegen dürfen um Störeffekte wie den Alias-Effekt zu vermeiden.
Beispielsweise wird bei Audio-CDs eine Abtastrate von 44,1 kHz benutzt, hingegen bei dem Digital Audio Tape (DAT) eine auch im Studiobereich und Rundfunkanstalten übliche Abtastrate von 48 kHz. Beide Abtastraten sind ausreichend um Audiosignale mit Frequenzen bis 20 kHz zu erfassen. Die Abtastratenkonvertierungen ist beispielsweise bei Überspielungen zwischen den beiden Abtastraten nötig.
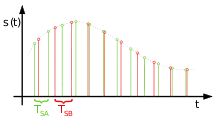
In nebenstehender Abbildung ist im Zeitbereich ein beispielhafter Signalverlauf mit zwei Signalfolgen mit unterschiedlichen Abtastraten, rot mit niedriger Abtastrate und grün mit höherer Abtastrate dargestellt. Die Information des Signals, in hellgrau hinterlegt, ist in beiden Fällen identisch. Liegt der Signalverlauf mit der niedrigeren Abtastrate 1/Tsb (in rot) vor, so werden mittels Interpolation die Zwischenwerte mit der neuen, höheren Abtastrate 1/Tsa (in grün) gebildet. Der Vorgang der Interpolation erfolgt mittels digitaler Filter, welche neben der nötigen Bandbegrenzung zur Erfüllung des Nyquist-Kriteriums auch die Berechnung der Zwischenwerte liefern. Jene Digitalfilter zählen, da sie mit unterschiedlichen Abtastraten arbeiten, zu den Multiratenfilter. Ein Beispiel eines einfachen Filters zur synchronen Abtastratenkonvertierung stellt das Cascaded-Integrator-Comb-Filter (CIC-Filter) dar.
Arten
Bei der Abtastratenkonvertierung wird zwischen zwei wesentlichen Anwendungsbereichen unterschieden:
- Synchrone Abtastratenkonvertierung (SRC) mit nominal unterschiedlichen aber zeitlich fixen Abtastraten. Dies ist üblicherweise dann der Fall, wenn von einer Taktquelle beide Abtastraten, beispielsweise einfache und doppelte Abtastrate, gebildet werden. Durch systembedingte Abweichungen und Toleranzen der Taktquelle ändern sich so beide Abtastraten im gleichen Verhältnis und die Relation zwischen beiden Abtastraten ist zeitlich fix.
- Asynchrone Abtastratenkonvertierung (ASRC) mit zeitlich nicht fixen Abtastraten. Dabei können, müssen aber nicht, die unterschiedlichen Abtastraten nominal gleich sein. Dies ist beispielsweise dann der Fall, wenn zwei unabhängige Taktquellen für die Erzeugung der Abtastfrequenz verwendet werden. Durch minimale und immer vorhandene Abweichungen, beispielsweise zufolge Temperatureinflüsse, kommt es dabei auch bei nominal gleichen Taktraten zu minimalen Abweichungen, die nach einiger Zeit zum Überspringen oder Duplizieren eines Abtastwertes und somit zu Fehlern führen würden. Der Fall der asynchronen Abtastratenkonvertierung ist technisch aufwändiger.
Bei der synchronen Abtastratenkonvertierung ist im Voraus immer der genaue Zeitpunkt bekannt, wo auf der Zeitachse ein bestimmter Abtastwert berechnet werden muss. Bei der asynchronen Abtastratenkonvertierung ist dies nicht möglich. In diesem Fall werden mittels laufender Zeitmessungen zwischen den beiden Abtastraten und daraus gebildeter Fehlersignalen zusätzlich notwendige Regelschleifen (englisch Digital Servo Loops) gesteuert, welche das laufende Nachjustieren und Verändern der Filterkoeffizienten in den Interpolationsfiltern vornehmen. Typischerweise kommen dabei Filterbänke in Polyphasenstruktur zur Anwendung.[1] Die Abtastraten dürfen sich dabei nicht zu schnell zeitlich verändern, um ein Nachführen der Regelstrecke zu gewährleisten.
Einzelnachweise
- AD1895 Audio Asynchronous Sample Rate Converter (PDF; 875 kB), Datenblatt, Analog Devices, 2002 (engl.)
Literatur
- Norbert Fliege: Multiraten-Signalverarbeitung. Teubner, 1993, ISBN 3-519-06155-4.