Cascaded-Integrator-Comb-Filter

Ein Cascaded-Integrator-Comb-Filter, abgekürzt CIC-Filter (engl. für kaskadiertes Integrator-Differentiator-Filter) ist in der digitalen Signalverarbeitung ein zeit- und wertdiskretes digitales Filter, das zur Abtastratenkonvertierung zwischen verschiedenen Abtastraten dient. Sie zählen zu der Gruppe der Multiratenfilter. Dieser Filtertyp wurde 1981 von Eugene Hogenauer entwickelt.[1]

Funktion

CIC-Filter sind ein spezieller Typ von FIR-Filtern und lassen sich sehr vorteilhaft in digitaler Hardware wie FPGAs (engl.: Field Programmable Gate Array) implementieren, da alle Koeffizienten des Filters „1“ und damit keine rechenintensiven Multiplikationen notwendig sind. Es kommen nur einfache Additionsstufen und Speicher, so genannte Taps, zur Anwendung. CIC-Filter dienen zur Umwandlung von digitalen Signalen zwischen Bereichen mit unterschiedlichen Abtastraten, welche ein fixes Abtastratenverhältnis zueinander aufweisen, und zur Vermeidung der dabei auftretenden Spiegelspektren bzw. zur Vermeidung von Aliasing.

Da im Filter alle Koeffizienten gleich „1“ sind, ist allerdings die Anpassung der Filtereigenschaften nur sehr eingeschränkt möglich. Die Varianten des Filters beschränken sich auf die Anzahl der einzelnen in Serie geschalteten Integrations- bzw. Differentiationsstufen, welche die Steilheit des Filters beschreiben und bei den Differentiationsstufen auf eine unterschiedliche Anzahl von Verzögerungsstufen (Taps), die die Bandbreite in sehr groben Schritten beeinflussen. In der Praxis werden daher öfter Kombinationen von CIC-Filtern mit anderen Filtern eingesetzt, um die gewünschten Übertragungseigenschaften als Summe der einzelnen Filter zu erhalten.

Varianten

Die CIC-Filter unterteilen sich in den Anwendungen in Interpolationsfilter und Dezimationsfilter.

Interpolationsfilter: Diese dienen dazu, eine diskrete Signalfolge von einer niedrigen Abtastrate auf eine höhere Abtastrate zu konvertieren. Die Signalwerte, die sich aufgrund der höheren Ausgaberate zwischen den Eingangsabtastwerten ergeben, werden interpoliert. Die bei der Aufwärtswandlung zwangsweise entstehenden Spiegelspektren im Ausgabebereich werden durch das CIC-Filter unterdrückt.

Dezimationsfilter: Diese Filter dienen dazu, von einer hohen auf eine niedrige Abtastrate zu wechseln. Dabei müssen alle Signalkomponenten des Eingabesignals, die über der halben Ausgabeabtastrate liegen, durch das Filter unterdrückt werden, um Aliasing zu vermeiden.

Filterstruktur

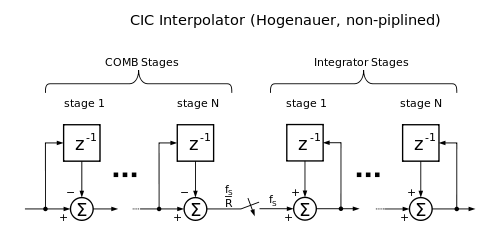
Die Struktur eines CIC-Filters, wie es als Interpolator verwendet wird. Der schematische Schalter in der Bildmitte stellt den eigentlichen Abtastratenwandler dar, die Blöcke links und rechts sind das Filter.

In nebenstehender Abbildung ist ein CIC-Interpolationsfilter abgebildet. Links erkennt man die einzelnen Differentiationsstufen, realisiert als Kammfilter, die in der Anzahl variieren können. Jede Stufe stellt einen Hochpass dar, der in seinem Frequenzgang mit ca. 6 dB pro Oktave ansteigt. Eingezeichnet ist nur ein Speicherregister (z⁻¹) pro Stufe. Eine Erhöhung auf zwei Speicherregister (z⁻²) würde eine Halbierung der Bandbreite bewirken. Daran anschließend in der Bildmitte ist der eigentliche Abtastratenwandler erkennbar, der in diesem Fall auf eine höhere Abtastrate konvertiert. Bei der Konvertierung werden Zwischenwerte durch den Wert 0 ersetzt. Die Stufen rechts sind die Integrationsstufen (Tiefpassfilter), ebenfalls in der Anzahl je nach Anwendung verschieden. Diese Stufen nehmen die Signalinterpolation für die Ausgangsfolge mit der hohen Abtastrate vor.

Ein CIC-Dezimationssfilter unterscheidet sich nur dahingehend, dass die Integrationsstufen mit den Differentiationsstufen in der Reihenfolge vertauscht werden.

Übertragungsfunktion

Die Übertragungsfunktion H(z) eines CIC-Filters, bezogen auf die Seite mit der hohen Abtastrate f_s, ist:

H(z)={\frac {(1-z^{-R\cdot M})^{N}}{(1-z^{-1})^{N}}}=\left[\sum _{k=0}^{R\cdot M-1}z^{-k}\right]^{N}

Wobei die Parameter bedeuten:

R = Dezimations- oder Interpolationsfaktor – Verhältnis der beiden Abtastraten zueinander.

M = Anzahl der Speicherregister (taps) pro Stufe. Typisch ist dieser Parameter 1, manchmal auch 2.

N = Anzahl der Stufen

Einzelnachweise

Eugene B. Hogenauer: An economical class of digital filters for decimation and interpolation. In: IEEE Transactions on Acoustics, Speech and Signal Processing. 2. Auflage. Nr. 29, April 1981, ISSN 0096-3518, S. 155–162, doi:10.1109/TASSP.1981.1163535.

Weblinks

CIC Filter Introduction

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[hogen1-1] Eugene B. Hogenauer: An economical class of digital filters for decimation and interpolation. In: IEEE Transactions on Acoustics, Speech and Signal Processing. 2. Auflage. Nr. 29, April 1981, ISSN 0096-3518, S. 155–162, doi:10.1109/TASSP.1981.1163535.