Ablaufsteuerung
Eine Ablaufsteuerung (englisch: sequential control) oder auch Schrittkette ist eine Steuerung, die schrittweise abläuft. Dieser Ablauf erfolgt zwangsläufig, wobei das Weiterschalten von Schritt A zu Schritt B durch Weiterschaltbedingungen (Transitionen) erfolgt, z. B. ein Zylinder fährt aus, transportiert ein Werkstück, dieses wird dann gespannt.
Der Entwurf von Ablaufsteuerungen kann nach DIN EN 60848 mit GRAFCET erfolgen, die Implementierung nach IEC 61131-3 mit Sequential Function Chart (SFC). Wird eine Ablaufsteuerung durch eine SPS realisiert, dann bietet sich zur Programmierung die Ablaufsprache an.
Beispiele für einfache Steuerungen und Ablaufsteuerungen
Eine einfache Steuerung ist zum Beispiel das Auslaufen von Wasser, nachdem der Wasserhahn geöffnet wurde. Dieser Zustand ändert sich erst, wenn eine weitere einfache Steuerung (schließen des Wasserhahns) vorgenommen wurde.
Eine einschrittige Ablaufsteuerung liegt vor, wenn das Schließen des Wasserhahns auf Grund einer Füllmeldung (feedback) Teil des Steuerprogramms ist.
In der Regel handelt es sich bei Ablaufsteuerungen um mehrere aufeinanderfolgende Schritte, die durch ein Steuerprogramm ausgeführt werden. Bei einem Waschautomaten werden Wasserzufluss und Wasserabpumpen, Waschmittelzugabe, Heizung und Trommelantrieb von einer Steuerung durch Verarbeitung von Informationen über Wasserstand, Temperatur und Zeit nach einem gewählten Programm derart in Gang gesetzt und angehalten, dass gereinigte und geschleuderte bzw. getrocknete Wäsche entsteht. Sensoren melden an die Steuerung zurück, dass die gewählten Werte für Wasserstand, Temperatur und Zeit erreicht sind, wonach der nächste Prozessschritt ausgelöst wird.
Definition der Ablaufsteuerung
Definition der Ablaufsteuerungen gemäß DIN IEC 60050-351
Für den Begriff Ablaufsteuerung existiert in der Norm DIN IEC 60050-351 die folgende Definition:
- Eine Ablaufsteuerung ist eine Steuerung mit einem schrittweisen Ablauf, bei dem der Übergang von einem Schritt auf den folgenden entsprechend der vorgegebenen Übergangsbedingung erfolgt.
Aus dieser Definition gehen allerdings die tatsächlichen Wirkungsabläufe von Ablaufsteuerung nicht hervor. Man kann nicht erkennen, wie die Steuergrößen dieser Steuerungsart beschaffen sind und in welcher Weise ihre Beeinflussung erfolgt. Daraus lässt sich auch nicht nachvollziehen, wie die „vorgegebenen“ Übergangsbedingungen zustande kommen.
Neuartiger Ansatz einer Definition von Ablaufsteuerungen
Zander[1] führt für die in Ablaufsteuerungen ablaufenden Vorgänge den Begriff „Ereignisdiskreter Prozess“ als Präzisierung des früher verwendeten Begriffs „Diskontinuierlicher Prozess“ ein, wobei er davon ausgeht, dass die Steuergrößen überwiegend analoge Größen sind, z. B. Drücke, Temperaturen, Füllstände, Wege, Winkel, Drehzahlen.
Ein wesentliches Merkmal dieser neuartigen Betrachtungsweise ist, dass während des Ablaufs eines ereignisdiskreten Prozesses die von der Steuereinrichtung ausgegebenen binären Stellsignale im Sinne von Sprungfunktionen auf die analogen Steuergrößen wirken und dass deren Funktionswerte sich dadurch im Sinne von Sprungantworten entsprechend dem jeweiligen Zeitverhalten ändern. So weist z. B. die Änderung des Füllstandes beim Füllen eines Behälters ein integrales Verhalten (I-Verhalten) auf.
Für die Steuergrößen sind entsprechende Schwellwerte festzulegen. Erreicht eine Steuergröße einen für sie vorgesehenen Schwellwert, dann wird das binäre Stellsignal, das die Veränderung der Steuergröße verursacht hat, von der Steuereinrichtung auf den Wert Null gesetzt. Gemäß dem in der Steuereinrichtung implementierten Steueralgorithmus wird dann das nächste Stellsignal ausgegeben und der nächste Schritt im Prozess ausgelöst.
Das Erreichen des Schwellwertes der Steuergröße wird als „Ereignis“ bezeichnet. Daraus erklärt sich der Name „Ereignisdiskreter Prozess“.
Ein Ereignis liegt auch vor, wenn eine Bedienhandlung ausgeführt wird oder eine vorgegebene Zeitdauer in einem Zeitglied abgelaufen ist. Beim Auftreten eines Ereignisses wird im Prozess definitionsgemäß ein Operationswechsel eingeleitet. Die Ereignisse werden zu diesem Zweck durch so genannte Ereignissignale an die Steuereinrichtung gemeldet. Ereignissignale sind also binäre Messsignale, binäre Bediensignale und binäre Ausgangssignale von Zeitgliedern.
Auf dieser Basis werden Ablaufsteuerungen, d. h. Steuerungen ereignisdiskreter Prozesse, nach Zander wie folgt definiert:
- Eine Ablaufsteuerung ist ein Vorgang, bei dem durch ein in der Steuereinrichtung eintreffendes Ereignissignal gemäß dem implementierten Steueralgorithmus ein binäres Stellsignal gebildet und dadurch eine Sprungfunktion auf eine analoge Steuergröße ausgeübt wird, so dass diese Steuergröße solange eine Sprungantwort ausführt und damit eine Operation abläuft, bis erneut ein auf sie bezogenes Ereignissignal eintrifft, das ein Beenden der laufenden Sprungantwort zur Folge hat und zum Aktivieren weiterer Sprungfunktionen der Steuereinrichtung führt usw.
- Kennzeichen von Ablaufsteuerungen sind ein geschlossener Wirkungsablauf durch Rückkopplung (feedback) und überwiegend analoge Steuergrößen.
Im Vergleich mit Regelungen beziehen sich die von Zander für die aus mehreren Schritten bestehenden Ablaufsteuerungen gewählten Begriffe geschlossener Wirkungsablauf und Rückkopplung auf andere, einfachere sachliche Zusammenhänge. Die Rückmeldung (feedback, geschlossener Wirkungsablauf) setzt lediglich die Steuergröße auf Null und die für den folgenden Teilprozess auf Eins. Es gibt keine Gegenkopplung einer analogen Ausgangsgröße (Istwert der Regelgröße) mit einer ebenfalls analogen Eingangsgröße (Sollwert).
Im Unterschied zu Ablaufsteuerungen werden in Verknüpfungssteuerungen nicht analoge Steuergrößen, sondern wertdiskrete (z. B. binäre) Steuergrößen als Ausgänge der Steuerstrecke in ihren Werten verändert. Dazu werden in der Steuereinrichtung durch logische Verknüpfung der binären Eingangssignale binäre Stellsignale erzeugt, die das Schalten der Steuergrößen bewirken. Eine Rückmeldung über eine ausgeführte Schalthandlung von den Ausgängen der Steuerstrecke zu den Eingängen der Steuereinrichtung existiert bei Verknüpfungssteuerungen nicht. Es liegt daher als Struktur des Informationsflusses eine offene Kette vor.
Beispiele für Verknüpfungssteuerungen sind Wechsel- und Kreuzschaltungen für das Ein- und Ausschalten von Leuchten oder Aggregaten durch Schalter an verschiedenen Orten.
Beschreibungsmittel und Fachsprachen für Ablaufsteuerungen
Als Beschreibungsmittel für Ablaufsteuerungen lassen sich steuerungstechnisch interpretierte Petri-Netze verwenden, wie diese von König und Quäck[2] ausgearbeitet wurden. In Frankreich wurde auf der Basis von Petri-Netzen die Beschreibungssprache GRAFCET geschaffen, die heute als DIN EN 60848 genormt ist.
Die wesentlichen Darstellungselemente von steuerungstechnisch interpretierten Petri-Netzen und von GRAFCET sind Schritte (auch Stellen oder Plätze genannt) und Transitionen. Den Schritten, die als „Zustände“ angesehen werden können, werden Aktionen (z. B. Ventil öffnen), und den Transitionen werden Übergangsbedingungen zugeordnet, durch die der Übergang von einem Schritt zum nächsten Schritt beschrieben wird.
Auf der Basis von Petri-Netzen und von GRAFCET wurden Ablaufsprachen zur Programmierung von speicherprogrammierbaren Steuerungen (SPS) entwickelt, deren Prototyp in der DIN EN 61131-3 als SFC (Sequential Function Chart) genormt ist. Beim Steuerungssystem STEP7 der Fa. Siemens wird die Ablaufsprache als „S7-GRAPH“ bezeichnet.
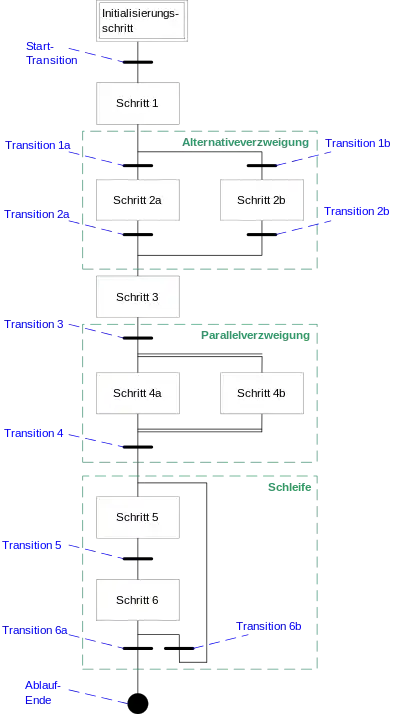
Der Initialisierungsschritt ist ein ausgezeichneter Wartezustand. Dieser wird verlassen, wenn die Starttransition für die Ablaufkette eintritt und der automatische Ablauf beginnt. Im Beispiel wird nach dem Schalten der Starttransition die Bearbeitung von Schritt 1 begonnen.
Neben dem linearen Ablauf von Schritten sind Alternativverzweigungen, Parallelverzweigungen und Schleifen modellierbar.
- Alternativverzweigung
Schritt 1 ist aktiv, bis Transition 1a oder 1b schaltet. Ist 1a wahr, so wird Schritt 1 beendet und Schritt 2a als Nächstes bearbeitet; Transition 1b führt zum Bearbeiten von Schritt 2b. Sind beide wahr, kommt eine Vorrangregel zum Zug, z. B. dass Schritt 2a bearbeitet wird.
- Parallelverzweigung
Schaltet Transition 3, wird Schritt 3 beendet und Schritt 4a und 4b werden gleichzeitig ausgeführt. Tritt Transition 4 ein, werden beide gleichzeitig beendet und die Ausführung von Schritt 5 begonnen.
- Schleife
Schritt 6 wird bearbeitet, bis 6a oder 6b eintritt. Ist Transition 6a wahr, wird in diesem Beispiel der Durchlauf der Ablaufkette komplett beendet. Tritt Transition 6b ein (und 6a ist nicht wahr), so wird Schritt 5 wieder bearbeitet.
Siehe auch
- IEC 61131 Teil 3
- Funktionsdiagramm
Literatur
- Ch. Duhr: Grafcet. Arbeitsheft. EUROPA-Lehrmittel Bildungsverlag, 2015, ISBN 978-3-8085-3763-3.
- R. König, L. Quäck: Petri-Netze in der Steuerungstechnik. Verlag Technik, Berlin 1988, ISBN 3-341-00525-0. (auch: Petri-Netze in der Steuerungs- und Digitaltechnik. Oldenbourg Verlag, München 1988)
- H.-J. Zander: Steuerung ereignisdiskreter Prozesse. Neuartige Methoden zur Prozessbeschreibung und zum Entwurf von Steuerungsalgorithmen. Springer Vieweg Verlag, Wiesbaden 2015, ISBN 978-3-658-01381-3.
Weblinks
- Der erste deutschsprachige Grafcet-Blog
- Vorlesung SPS-Ablaufsteuerung (Memento vom 6. September 2012 im Internet Archive), S. 121, Kapitel 5, Wagner, 2006, Uni Hannover (PDF-Datei, 51 kB)
- Ablaufsteuerungen, Ablaufsprache S7-Graph und zugehörige Beschreibungsarten gemäß IEC1131-3 (Memento vom 25. November 2012 im Internet Archive), Schumacher, 2007, FH OOW/Wilhelmshaven (PDF-Datei, 250 kB)
Einzelnachweise
- H.-J. Zander: Steuerung ereignisdiskreter Prozesse. Neuartige Methoden zur Prozessbeschreibung und zum Entwurf von Steuerungsalgorithmen. Springer Vieweg Verlag, Wiesbaden 2015, ISBN 978-3-658-01381-3, S. 38–43 und S. 185–192.
- R. König, L. Quäck: Petri-Netze in der Steuerungstechnik. Verlag Technik, Berlin 1988, ISBN 3-341-00525-0.