Abbesche Invariante

Die Abbesche Invariante (nach Ernst Abbe; auch Invariante der Brechung, Nullvariante)[1] stellt in der paraxialen Optik den Zusammenhang zwischen objektseitiger und bildseitiger Schnittweite von Lichtstrahlen dar, die an einer Fläche gebrochen werden:[2]

n\left({\frac {1}{r}}-{\frac {1}{s}}\right)=n'\left({\frac {1}{r}}-{\frac {1}{s'}}\right)

mit

n, n' = Brechungsindex vor bzw. nach der brechenden Fläche (jeweils ' für die Bildseite)
r = Krümmungsradius der brechenden Fläche
s, s' = objektseitige bzw. bildseitige Schnittweite.

Die Gleichung besagt, dass die lineare Beziehung zwischen Brechungsindex, Krümmungsradius und Schnittweite vor und nach der Brechung eine konstante Größe behält.[3]

Diese Invariante ist eine Grundlage für die Ableitung aller Gesetzmäßigkeiten der optischen Abbildung im achsnahen Gebiet.[3]

Eine andere diesbezügliche Grundaussage ist die Helmholtz-Lagrangesche Invariante.

Herleitung

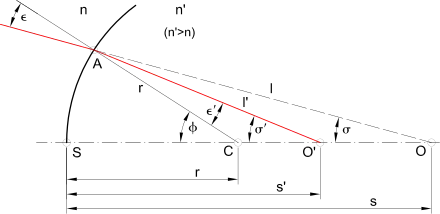
Herleitung der Abbeschen Invariante

In den Dreiecken ACO und ACO' bestehen folgende Beziehungen nach dem Sinussatz:

{\frac {\sin \epsilon }{\sin(180^{\circ }-\phi )}}={\frac {s-r}{l}}

und

{\frac {\sin \epsilon '}{\sin(180^{\circ }-\phi )}}={\frac {s'-r}{l'}}

.

Die erste durch die zweite Beziehung geteilt:

{\frac {\sin \epsilon }{\sin \epsilon '}}={\frac {l'(s-r)}{l(s'-r)}}

.

Mit dem Brechungsgesetz n sinε = n' sinε' :

n\left({\frac {s-r}{l}}\right)=n'\left({\frac {s'-r}{l'}}\right)

.

Im paraxialen Gebiet sind die Winkel σ und σ' so klein, dass für die Strahllängen l und l' die Schnittweiten s bzw. s' gesetzt werden können. Damit erhält man:

n\left({\frac {1}{r}}-{\frac {1}{s}}\right)=n'\left({\frac {1}{r}}-{\frac {1}{s'}}\right)

.

Einzelnachweise

Lexikon der Physik, Abbesche Invariante. Spektrum.de, abgerufen am 6. April 2014.
Heinz Haferkorn: Optik: Physikalisch-technische Grundlagen und Anwendungen, Barth, 1994, ISBN 3-335-00363-2, S. 185/86
Fritz Hodam: Technische Optik, VEB Verlag Technik, 2. Auflage, 1967, S. 42

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Lexikon der Physik, Abbesche Invariante. Spektrum.de, abgerufen am 6. April 2014.

[Hafer-2] Heinz Haferkorn: Optik: Physikalisch-technische Grundlagen und Anwendungen, Barth, 1994, ISBN 3-335-00363-2, S. 185/86

[Hodam-3] Fritz Hodam: Technische Optik, VEB Verlag Technik, 2. Auflage, 1967, S. 42