Zyklische Faltung

Die zyklische Faltung, auch als zirkulare Faltung oder als periodische Faltung bezeichnet, ist in der Funktionalanalysis eine Form der diskreten Faltung. Dabei werden Folgen der Länge $N$ periodisch fortgesetzt, welche sich durch die zyklische Verschiebung der Folge ergeben. Anwendung der zyklischen Faltung liegen primär in der digitalen Signalverarbeitung, beispielsweise zur Realisierung von digitalen Filtern.

Allgemeines

Vergleich diskrete aperiodische Faltung, linke Spalte, und rechts diskrete zyklische Faltung

In Kombination mit der diskreten Fourier-Transformation (DFT), insbesondere der schnellen Fourier-Transformation (FFT), kann mit der zyklischen Faltung die rechenintensive diskrete aperiodische Faltungsoperation im Zeitbereich durch eine effizientere Multiplikation im Spektralbereich ersetzt werden. Die periodische Faltung hat in dem blockbasierenden Aufbau des FFT-Algorithmus ihren Ursprung.

Zur Bildung der schnellen Faltung wird die zyklische Faltung durch schnelle Fouriertransformation und Verfahren wie dem Overlap-Save-Verfahren oder Overlap-Add-Verfahren erweitert, mit dem Ziel nichtrekursive Digitalfilter (FIR-Filter) höherer Ordnung effizient zu realisieren. Herkömmliche FIR-Filter in der direkten Normalform führen unmittelbar die aperiodische Faltungsoperation aus, welche ab ca. 50 Filterordnung ineffizienter als die schnelle Faltung ist.

Die zyklische Verschiebung um $m$ Stellen einer Folge $x[n]$ der Länge $N$ kann mit der Modulooperation ausgedrückt werden:

{\tilde {x}}[n-m]=x[(n-m){\bmod {N}}]

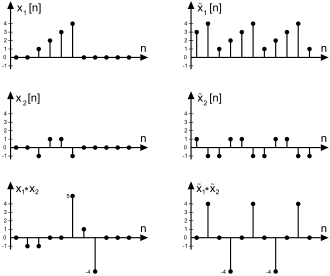
wobei periodisch fortgesetzte Folgen mit dem Tildesymbol gekennzeichnet sind. In nebenstehender Abbildung sind links zwei beispielhafte Folgen $x_{1}$ und $x_{2}$ der Länge $N=4$ und deren aperidoisches Faltungsergebnis dargestellt. Rechts dazu deren periodisch fortgesetzten Folgen ${\tilde {x}}_{1}$ und ${\tilde {x}}_{2}$ und das daraus gebildete zyklische Faltungsprodukt ${\tilde {x}}_{1}*{\tilde {x}}_{2}$ .

Literatur

Alan V. Oppenheim, Ronald W. Schafer: Zeitdiskrete Signalverarbeitung. 3. Auflage. Oldenbourg, 1999, ISBN 3-486-24145-1.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.