Zone (Kristallographie)
Unter einer Zone versteht man in der Kristallographie eine Schar von Ebenen, deren Schnittkanten parallel verlaufen. Die Ebenen, die einer Zone angehören heißen tautozonal. Die Richtung der Schnittkante wird als Zonenachse bezeichnet. Die Normalenvektoren tautozonaler Ebenen liegen in einer Ebene auf der die Zonenachse senkrecht steht. Zwei sich schneidende Ebenen bestimmen eine Zone eindeutig, da die Schnittgerade die Zonenachse ist.
Die Zonenachsen sind Gittervektoren des realen Gitters. Sie werden daher wie Punkte des realen Gitters durch eckige Klammern bezeichnet: [uvw]. Im Gegensatz dazu werden die millerschen Indizes der Ebenen in runden Klammern geschrieben: (hkl). Der Zone im realen Raum entspricht im reziproken Raum eine Ebene:
| Bezeichnung | Reales Gitter | Reziprokes Gitter | |
|---|---|---|---|
| Netzebene | (hkl) | Ebene | Punkt |
| Zone | [uvw] | Punkt | Ebene |
Die Zonengleichung
Den Zusammenhang zwischen einer Ebene (hkl) und einer Gerade [uvw] beschreibt die Zonengleichung:
- .
Diese Gleichung ist genau dann erfüllt, wenn die Gerade [uvw] in der (hkl)-Ebene liegt, bzw. wenn die Ebene (hkl) zur Zone [uvw] gehört.
Beispiel
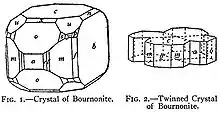
Das Bild zeigt eine schematische Darstellung der idiomorphen Flächen von Bournonit. In den Flächen a, e ,l ,m ,f und b gibt es eine für alle Flächen gemeinsame Richtung, die senkrecht zur c-Fläche verläuft. Daher gehören alle diese Flächen zu der [001]-Zone.
Anwendungen
Die stereographische Projektion der Ebenen einer Zone bilden einen Großkreis im wulffschen Netz. So kann man mit Hilfe des wulffschen Netzes bevorzugte Richtungen im Kristall bestimmen. In der Regel entsprechen diese Richtungen Achsrichtungen des Kristallgitters.
Die von den Netzebenen einer Zone gebeugten Röntgenstrahlen liegen auf einem Kegel, dessen Achse die Zonenachse ist. Der Öffnungswinkel wird durch die Gitterkonstante der Zonenachse bestimmt. Daher können alle anderen Strahlen durch eine Kreisblende ausgeblendet werden. Dies wird beim Weissenberg-, Buerger- und beim De-Jong-Bouman-Verfahren ausgenutzt.
Literatur
- D. Schwarzenbach: Kristallographie Springer Verlag, Berlin 2001, ISBN 3-540-67114-5.
- Will Kleber, Hans-Joachim Bautsch, Joachim Bohm, Detlef Klimm: Einführung in die Kristallographie. 19. Auflage. Oldenbourg Wissenschaftsverlag, 2010, ISBN 978-3-486-59075-3.
- Walter Borchard-Ott: Kristallographie 7. Auflage, Springer Verlag, Berlin 2009, ISBN 978-3-540-78270-4.
- Lothar Spieß, et al.: Moderne Röntgenbeugung 3. Auflage, SpringerSpektrum, Wiesbaden 2019 ISBN 978-3-8348-1219-3.