Wechselwirkungsfreie Quantenmessung
In der makroskopischen und „traditionellen“ mikroskopischen Welt verursacht jede Messung eine Störung des beobachteten Zustands. Jedoch erlauben Quanteneffekte in der mikroskopischen Welt der Quanten, Objekte erkennen zu können, ohne diese auch nur einem einzigen Lichtquant aussetzen zu müssen. Dadurch wird das zu messende Objekt nicht verändert. Dieser Vorgang wird als wechselwirkungsfreie Quantenmessung bezeichnet.
Sie wurde zuerst 1993 in einem Gedankenexperiment von Avshalom Elitzur und Lev Vaidman vorgeschlagen und experimentell 1994 von einer Gruppe um Anton Zeilinger erstmals demonstriert.[1]
Vorgeschichte
Dennis Gábor, der Entdecker der Holografie, hat 1962 die Behauptung aufgestellt, dass sich ein Gegenstand nur beobachten lässt, wenn dieser Gegenstand von mindestens einem Photon, d. h. einem Lichtquant, getroffen wird.
In der klassischen Vorstellung von Photonen als Teilchen ist dies auch durchaus richtig und dient auch heute noch als das gängige Erklärungsmodell. In der Quantenphysik lässt sich dieses Problem jedoch teilweise umgehen.
Gedankenexperimente
Ein bekanntes Gedankenexperiment findet sich in der griechischen Mythologie. Hier stand Perseus vor der Aufgabe Medusa zu töten. Das Problem dabei war, dass jeder, der Medusa ansah, zu Stein erstarrte. Mit geschlossenen Augen war es einem Angreifer kaum möglich Medusa zu lokalisieren. Perseus löste dieses Problem, indem er Medusa seinen glänzenden Schild vorhielt, sodass Medusa sich selbst sah und erstarrte.
Als weiteres Beispiel sei das Hütchenspiel erwähnt. Hierbei ist ein kleiner Gegenstand (z. B. eine Murmel) unter einem von mehreren Hütchen versteckt und kann von einem Beobachter nicht erkannt werden. Im Gedankenexperiment soll dieser Gegenstand zu Staub zerfallen, sobald man das Hütchen abnimmt und der Gegenstand ins Licht kommt.
Die wechselwirkungsfreie Quantenmessung kann diese Probleme lösen. Mit der wechselwirkungsfreien Quantenmessung könnte man beim Hütchenspiel immer gewinnen. Perseus wäre es möglich gewesen, Medusa zu lokalisieren ohne sie zu betrachten.
Das Doppelspaltexperiment
Das Prinzip der wechselwirkungsfreien Quantenmessung nutzt die Welleneigenschaft des Lichts aus. Wenn sich zwei solcher Wellen überschneiden, entsteht eine Interferenz, wie dies aus dem Doppelspaltexperiment ersichtlich ist. Im Teilchenmodell ist ein heller Streifen auf dem Schirm hinter dem Spalt eine Stelle, an der ein Photon mit hoher Wahrscheinlichkeit auftritt; ein dunkler, wenig belichteter Streifen auf dem Schirm hingegen ist eine Stelle, an der ein Photon mit niedriger Wahrscheinlichkeit auftritt.
Nach den Prinzipien der Quantenmechanik tritt eine Interferenz bei einem einzelnen Lichtstrahler wie im Doppelspaltexperiment nur auf, wenn es mehr als einen Weg gibt, den ein Photon nehmen kann, um an einen bestimmten Ort zu gelangen.
Beim Doppelspaltexperiment können die Lichtquanten entweder durch den einen oder den anderen Spalt fliegen. Wenn man feststellen kann, welchen Weg ein Lichtquant nimmt, so entsteht kein Streifenmuster, sondern abwechselnd eine Beleuchtung von der einen und dann der anderen Seite.
Elitzur-Vaidman-Schema
Die Physiker A. C. Elitzur und L. Vaidman von der Universität Tel Aviv in Israel haben sich in ihrem Gedankenexperiment eine Bombe vorgestellt, die beim Auftreffen eines Quants explodiert[2]. Es gelang ihnen, eine Methode zu entwickeln, die in der Hälfte aller Messungen wechselwirkungsfrei ist. Die Versuchsanordnung wird auch als Knallertest oder Bombentest bezeichnet.[3]
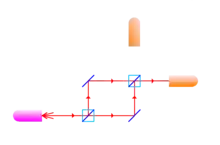
Bei dem von Vaidman und Elitzur erdachten Verfahren durchläuft das Photon ein Mach-Zehnder-Interferometer. Dabei wird der Photonenstrahl eines Lasers mit Hilfe eines halbdurchlässigen Spiegels in zwei Strahlen aufgeteilt. Über zwei Umlenkspiegel treffen die beiden Strahlen anschließend wieder in einem weiteren halbdurchlässigen Spiegel zusammen und können damit interferieren. Das Mach-Zehnder-Interferometer ähnelt in dieser Hinsicht also dem Doppelspaltexperiment.
Strahlengang ohne Objekt
Die obere Abbildung zeigt den Strahlenverlauf ohne Objekt im Strahlengang. Der im zweiten Strahlteiler reflektierte Teil des unteren Strahls vereint sich mit dem von links passierenden Teil des oberen Strahls und trifft auf den rechten Detektor. Der im zweiten Strahlteiler passierende Teil des unteren Strahls vereint sich aber auch mit dem nach oben reflektierten Teil des oberen Strahls und trifft auf den oberen Detektor. Bei geeigneter Dimensionierung des Interferometers kommt es zur Interferenz der zusammentreffenden Strahlen. Dabei verstärken sich die Strahlen in Richtung des rechten Detektors etwa bis zur Intensität der Quelle, in Richtung des oberen Detektors hingegen löschen sie sich aus. Hervorgerufen wird dies durch eine unterschiedliche Anzahl von reflexionsbedingten Phasenverschiebungen der Strahlengänge. Die Reflexionen an den Halbspiegeln verschieben die Phase des Lichts nur dann um 180°, wenn das Licht direkt auf die Grenzfläche zwischen Vakuum und Silberbeschichtung fällt. Trifft das Licht erst nach Durchqueren des Glasträgers auf die Silberbeschichtung, so findet keine Phasenverschiebung statt. Bei entsprechender Ausrichtung der Halbspiegel trifft im oberen Detektor um 360° phasenverschobenes Licht auf um 180° phasenverschobenes Licht; die Phasenverschiebung der zwei Strahlen zueinander beträgt demnach 180° und sie interferieren destruktiv.
Klassisch betrachtet tritt hier der Wellencharakter des Lichts in den Vordergrund. Quantenmechanisch gesehen ist es objektiv unbestimmt, welchen Weg ein Photon nimmt, solange dies nicht durch eine Messung festgestellt wird.
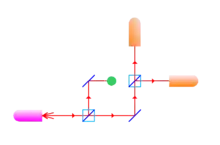
Strahlengang mit Objekt
In der unteren Abbildung wird ein lichtundurchlässiges Objekt in den oberen Lichtstrahl eingefügt. Dadurch wird verhindert, dass der obere Lichtstrahl beim zweiten halbdurchlässigen Spiegel eintrifft. Somit entsteht keine Wechselwirkung zwischen den beiden Lichtstrahlen. Somit erreicht nur der untere Lichtstrahl den zweiten Strahlteiler und wird dort zu gleichen Teilen aufgeteilt. Damit sprechen beide Detektoren mit gleicher Intensität an.
Alternativ kann das Photon auch als Teilchen betrachtet werden. Im ersten Strahlteiler nimmt das Photon dann mit einer Wahrscheinlichkeit von 50 % entweder den unteren Weg oder den oberen Weg. Wenn das Photon den oberen Weg nimmt, trifft es auf das Messobjekt und wird absorbiert. Das Photon erreicht dann keinen der beiden Detektoren. Nimmt das Photon den unteren Weg, kann es wieder auf beide Detektoren treffen, da das Photon ab dem oberen halbdurchlässigen Spiegel beide Wege nehmen kann.
Das Anschlagen des rechten Detektors entspricht nun dem Ergebnis ohne Objekt im oberen Strahlengang und lässt somit keinen Rückschluss auf das Vorhandensein des Objektes zu. Schlägt hingegen der obere Detektor an, hat das Photon zwar den unteren Weg ohne Wechselwirkung gewählt, konnte jedoch den zweiten Halbspiegel geradeaus durchqueren. Diese Möglichkeit konnte vorher durch die Interferenz der Strahlengänge nicht realisiert werden.
Das einzelne Photon ist also nicht mit dem Objekt in Wechselwirkung getreten. Es ist nicht einmal in dessen Nähe gekommen. Dennoch weist das Photon durch das geänderte Verhalten am zweiten Strahlteiler die Existenz des Objekts nach.
Durch Anpassen der Reflektivitäten der Halbspiegel kann die Trefferquote von 25 % überschritten werden.
| Objekt | Wechselwirkung | Detektor oben | Detektor rechts | Wahrscheinlichkeit |
|---|---|---|---|---|
| nicht vorhanden | nein | dunkel | hell | 100 % |
| vorhanden | ja | dunkel | dunkel | 50 % |
| nein | hell | dunkel | 25 % | |
| nein | dunkel | hell | 25 % | |
Literatur
- Paul Kwiat, Harald Weinfurter, Anton Zeilinger: Wechselwirkungsfreie Quantenmessung. In: Spektrum der Wissenschaft. Nr. 1, 1997, S. 42–49 (Vorschau).
Einzelnachweise
- Zeilinger, Harald Weinfurter, Paul G. Kwiat, Thomas Herzog, Mark A. Kasevich Interaction-free Measurement, Physical Review Letters, Band 74, 1995, S. 4763, Abstract
- Elitzur, Vaidman Quantum mechanical interaction free measurement, Foundations of Physics, Band 23, 1993, S. 987–997
- Beispiel: Dorn/ Bader Physik 12/13 Gymnasium Sek II, 2000, S. 250f