Unschärfe (Sprache)

Von der Unschärfe eines sprachlichen Begriffs spricht man, wenn es schwierig ist, ihn eindeutig einer bestimmten lexikalischen oder grammatischen Kategorie zuzuordnen. In der Linguistik werden dafür im Allgemeinen die Begriffe „Vagheit“ oder (auch außerhalb des englischen Sprachraums) „Fuzziness“ gebraucht:

„Wir sprechen von der V a g h e i t (syn.: Unschärfe, Verschwommenheit; engl.: fuzziness, vagueness) eines natürlichsprachlichen Ausdrucks [bzw. eines Begriffs], wenn es für bestimmte Anwendungsbereiche und -situationen keine eindeutigen Konventionen dafür gibt, ob der Ausdruck zur Bezeichnung eines bestimmten Gegenstands, Sachverhaltes oder Prozesses benutzt werden kann oder ob seine Verwendung ausgeschlossen ist, oder wenn bestimmte potentiell relevante Aspekte der Aussage, die durch den Ausdruck formuliert wird, offen bleiben.“[1]

Danach ist ein Begriff „unscharf“ („vage“ oder „fuzzy“),

wenn der Begriffsumfang (die Extension) ungenau ist;
wenn es Objekte gibt, von denen nicht mit Bestimmtheit gesagt werden kann, ob sie zu der Menge von Objekten gehören, die mit diesem Begriff bezeichnet werden oder die mit dessen Prädikaten bezeichneten Eigenschaften aufweisen (Grenzfälle der Kategorisierung).

Darüber hinaus spricht man von „Unschärfe“ („Vagheit“ oder „Fuzziness“) oft auch, wenn ein Begriff oder ein Prädikat ein Phänomen bezeichnet, auf das die Sorites-Paradoxie zutrifft.

Zum Begriff „Begriff“

In der Linguistik/Psycholinguistik sowie in der Psychologie versteht man unter einem „Begriff“ oder „Konzept“ (engl. concept) eine gedankliche Zusammenfassung einzelner Entitäten (Objekte, Sachverhalte, Ereignisse oder Relationen), die gemeinsame Merkmale aufweisen („Klassifizierung“; vgl. auch Kategorisierung). Mit anderen Worten: Durch Klassifizierung (auch: Klassifikation) werden „gegebene Objekte hinsichtlich bestimmter Merkmale und Strukturen identifiziert und einer bestimmten Klasse oder Unterklasse zugeordnet“.[2] So definiert auch Hadumod Bußmann einen „Begriff“ als ein „[d]urch Abstraktion [vielfältigster Erfahrungen] gewonnenes gedankliches Konzept, durch das Gegenstände oder Sachverhalte aufgrund bestimmter Eigenschaften und/oder Beziehungen klassifiziert werden“.[3] Ein Begriff oder Konzept ist „demnach eine kognitive Einheit, die aus der Verarbeitung von Informationen resultiert.“[4]

Unscharfer Umfang (Extension) von Begriffen

Ein Begriff kann zunächst durch seinen Umfang (seine Extension) definiert werden, d. h. die Gesamtheit aller Objekte, die sämtliche Merkmale dieses Begriffs haben. Diese „Gesamtheit“ ist in vielen Fällen jedoch nicht eindeutig bestimmbar. So werden viele Begriffe wie „Mittelklassewagen“, „groß“, „blau“ oder „grob fahrlässig“ unscharf gebraucht. So mag etwa ein Auto eines bestimmten Typs gemeinhin als ein (Element der Klasse) „Kompaktwagen“ gelten, während es für viele Betrachter bereits ein Wagen der „Mittelklasse“ ist. In ähnlicher Weise kann ein Baby für die Eltern schon „groß“ sein, dennoch ist es klein im Vergleich mit einem Schulkind; auch kann eine Person eher groß für einen Betrachter und eher nicht groß für einen anderen Betrachter sein. Dies ist unabhängig davon, ob die Betrachter nur die ungefähre oder exakte Größe einer Person kennen.

Kommunikative Konflikte, die sich aus der Verwendung unscharfer Begriffe – z. B. „blau“ – ergeben, werden meist durch „Aushandeln“ bzw. nachträgliche (begriffliche) Klarstellung gelöst oder als Grenzfälle akzeptiert:

A: Das blaue Auto gefällt mir.
B: Welches blaue Auto?
A: Na das da hinten, das dritte von rechts.
B: Das ist doch grün.
A: Na schön, das blaugrüne Auto da würde ich jedenfalls gerne haben, wenn ich es mir leisten könnte.

Ob ein bestimmtes Handeln „grob fahrlässig“ war oder nicht, kann dagegen oft nur durch ein gerichtliches Aushandeln zwischen Staatsanwalt, Verteidiger und Gutachter geklärt werden.

Es sind also nicht die „Phänomene“ (das Auto, das Baby, ein bestimmtes Handeln), die „unscharf“ oder „vage“ sind, sondern ihre Klassifizierung durch den Betrachter (als „Mittelklassewagen“, „blau“, „groß“ oder „grob fahrlässig“). Überspitzt ausgedrückt: „Vagheit ist keine Eigenschaft von Begriffen, sondern eine falsche Interpretation von nicht-vagen Phänomenen.“[5]

Unscharfe Abgrenzung von Begriffen

Der unscharfe Umfang eines Begriffs kann auch als unscharfe Abgrenzung dieses Begriffs von anderen Begriffen beschrieben werden. Während zum Beispiel manche Gegenstände eindeutig als „Stuhl“ oder als „Sessel“ wahrgenommen bzw. bezeichnet werden[6], erscheinen andere, z. B. ein Schaukel- oder ein Schreibtischstuhl, eher als „ein Mittelding“ zwischen einem Stuhl und einem Sessel. Die Kategorisierung eines solchen Gegenstandes ist nicht eindeutig (crisp), sondern „unscharf“ oder „verschwommen“ (fuzzy). In gleicher Weise sind auch grammatische Kategorien wie „Vergangenheit“, „abgeschlossene Handlung“ oder „Bezug zur Gegenwart“ nicht eindeutig definiert, also unscharf.[7]

Der Fachbegriff Fuzziness stammt ursprünglich aus der Mathematik bzw. der Kybernetik (Fuzzylogik) (Zadeh 1965). Wenn er nicht, wie in der Definition am Beginn dieses Artikels, gleichbedeutend mit Vagheit gebraucht wird, bezeichnet er explizit die „kontinuierliche“ oder „graduelle“ Klassenzugehörigkeit von Entitäten zu sprachlichen Begriffen, die mathematisch erfasst werden kann. Ein Rotkehlchen gehört demnach eher zur Klasse der „Vögel“ als ein Pinguin, der zwar viele Merkmale eines „Vogels“ aufweist, nicht jedoch das Merkmal „kann fliegen“, und dennoch biologisch ein „Vogel“ ist.

Psychologisch stellen sich diese Sachverhalte folgendermaßen dar: Alle Phänomene der Welt („Objekte“), die wir wahrnehmen, also Gegenstände, Vorgänge, Farben, Laute usw., werden nie als Objekte an sich wahrgenommen, sondern immer als Realisationen bestimmter, unserer Erfahrung entstammender Abstraktionen, die als Klassen von Objekten beschrieben werden können („Kategorisierung“). Damit ist auch die Bedeutung eines Ausdrucks wie Stuhl „nicht eine individuelle Vorstellung; sie ergibt sich aus der Ähnlichkeit der Einzelvorstellungen als soziales Phänomen …“.[8] Ein konkretes Objekt als „Stuhl“ wahrzunehmen heißt also, es als Element der Klasse „Stühle“ zu erkennen. Dabei werden unbewusst Fragen wie die folgenden beantwortet: Welche Eigenschaften muss der Stuhl aufweisen, damit er als solcher erkannt und dementsprechend bezeichnet werden kann? Welche Funktion(en) muss er erfüllen? Wie eben und wie waagrecht muss die Sitzfläche sein? Wie viele Beine muss bzw. darf er haben und wie hoch müssen bzw. dürfen diese sein? Die entsprechenden Voraussetzungen für einen „Stuhl“ bzw. einen „Nicht-Stuhl“ sind offensichtlich konventionalisiert, sie entsprechen intuitiven Vorstellungen. Grenzfälle ordnen wir intuitiv entweder der einen oder der anderen Kategorie zu oder machen gerade diesen Grenzfall-Charakter zum Thema („Aushandeln“ von Bedeutungen wie in den obigen Beispielen des „blauen“ Autos bzw. der „groben Fahrlässigkeit“).

Muttersprachliche bzw. sonst wie kompetente Sprecher einer Sprache verfügen jedenfalls über sehr viel mehr und sehr viel detailliertere intuitive Kenntnisse des Wortschatzes oder der Grammatik (der Regularitäten) dieser Sprache, als sich in einer linguistischen Sprachbeschreibung festlegen lassen. In diesen Sprachkenntnissen verbinden sich ganz unbewusst die bisher gemachten Lebenserfahrungen mit den damit verknüpften sprachlichen Erfahrungen (vgl. Sprachgefühl).

Übrigens treffen auch außerhalb des Sprachgebrauchs Experten auf einem bestimmten Gebiet, z. B. ein Handwerker oder eine Hausfrau, die bei vielen ihrer Entscheidungen ihrer (erfahrungsgestützten) Intuition folgen, nicht immer scharfe Ja-Nein-Entscheidungen. Oft entscheiden sie, wie ein fuzzy-logisches Computerprogramm zur Steuerung eines technischen Geräts, auf der Grundlage von graduellen Ausprägungen bestimmter Kriterien (mehr Flüssigkeit, etwas Öl, eine Handvoll Mehl), handeln also intuitiv und sind damit in aller Regel auch erfolgreich.

Die Sorites-Paradoxie – Die Unschärfe des „Haufens“

An dieser Stelle sei noch ein Sonderfall von „Unschärfe“ angeführt: die Sorites-Paradoxie (Paradoxie des Haufens). Sie zeigt sich beim Versuch, etwas als „Haufen“ zu bestimmen.[9] Entfernt man z. B. von einem Sandhaufen ein einzelnes Sandkorn, so bleibt immer noch ein Haufen; ebenso, wenn man ein weiteres Korn entfernt. Da es keine Abbruchsbedingung bzw. keinen Umschlagspunkt gibt, führt dies streng genommen dazu, dass ein einziges Sandkorn ebenfalls einen Haufen bildet. Gleiches gilt für ein „großes“ Objekt, das man Millimeter für Millimeter verkleinert. Die Ursache der Paradoxie des Haufens liegt darin, dass die Gestalt eines Haufens nicht durch die Anzahl seiner Elemente bestimmt und prinzipiell auch nicht bestimmbar ist. Andererseits sagt uns unsere Lebenserfahrung, zu der auch der Sprachgebrauch unserer Mitmenschen gehört, dass ein einziges Sandkorn und auch fünf oder zehn Sandkörner keinen „Sandhaufen“ bilden. Irgendwo beginnt aber sicher eine Grauzone, innerhalb derer wir von „Grenzfällen“ sprechen können. Logisch-definitorisch und damit eindeutig lässt sich die Sorites-Paradoxie jedenfalls nicht lösen.

Sprachliche Unschärfe in der Linguistik

Für die Erklärung und Beschreibung von sprachlicher Unschärfe gibt es eine Reihe von Ansätzen. Die bisher einflussreichsten sind:

Prototypensemantik

Die Prototypensemantik als Theorie der Wortbedeutung (lexikalische Semantik) stellt einen inzwischen generell akzeptierten Erklärungsansatz für bestimmte Vagheitsphänomene bereit: Begriffe oder begriffliche Kategorien werden nicht als Bedeutungsräume mit fest umrissenen Grenzen beschrieben, sondern als eine Art topologischer Raum mit einem Kern – z. B. dem „Küchenstuhl“, den wir als Prototypen eines „Stuhls“ ansehen können – und fließenden Übergängen zu einer Peripherie, zu der z. B. „Hochstuhl“, „Drehstuhl“ oder „Schaukelstuhl“ gehören.

Nach György Fuhrmann ist ein „Prototyp“ das maximal repräsentative Element einer bestimmten Kategorie.[10] So ist ein Küchenstuhl sicher ein maximal repräsentativer Vertreter der Kategorie „Stuhl“, während ein Hochstuhl zwar ebenfalls ein (peripherer) Repräsentant der Kategorie „Stuhl“ ist, aber keiner der (sehr viel kleineren) Kategorie „typischer Stuhl“. Ein „Hocker“ ist demgegenüber eigentlich kein Stuhl, aber „irgendwie“ ist er doch näher am Stuhl als z. B. ein „Fahrstuhl“. Dort, an der Peripherie, mag er für manche immer noch ein Element der (unscharfen) Kategorie „Stuhl“ sein, während ihn andere bereits außerhalb dieser Kategorie und damit als Element eines anderen „topologischen Raums“ sehen. Als Grenzfall kann der „Hocker“ jedenfalls Anlass zu Diskussionen über seine Klassenzugehörigkeit geben. Je ferner, also unähnlicher, ein Objekt dem Prototyp des Begriffs ist, umso unklarer oder umstrittener ist die Zuordnung dieses Objekts zum Begriff. „Generell erscheint uns das Zentrum einer Kategorie als fest etabliert und eindeutig. Die Grenzfälle von Kategorien sind nicht so eindeutig und klar, an den Rändern sind Kategorien tendenziell unscharf oder fuzzy und überschneiden sich mit angrenzenden Kategorien.“[11]

Die Vagheit von Wortbedeutungen wie groß, unreif, kühl oder jung lässt sich allerdings nicht mithilfe der Prototypensemantik erklären. Hierfür können einerseits Formalismen der Fuzzylogik herangezogen werden, während man seit den 1990er Jahren zunehmend auch auf kontextuelle Faktoren, d. h. die Kontextabhängigkeit von Begriffen, zurückgreift (s. unten).

Die Theorie der unscharfen Mengen („fuzzy sets“)

Seit Mitte der 1970er Jahre[12] hat man für die Erklärung der „Unschärfe“ sprachlicher Begriffe und Regeln sowie auch des intuitiven „Sprachgefühls“ auf den Ansatz der Fuzzylogik mit deren Konzept der „unscharfen Mengen“ (auch: Mengen mit „unscharfen Grenzen“) zurückgegriffen.

In der Sprache der – stark vereinfachten – Fuzzy-Set-Theorie hat ein eindeutig erkannter Stuhl (z. B. ein Küchen- oder ein Esszimmerstuhl) in Bezug auf die Kategorie (oder Menge) „Stuhl“ eine Klassenzugehörigkeit von „1“ und ein Gegenstand, der eindeutig kein Stuhl ist (z. B. ein Fahrstuhl), den Wert „0“. „Zugehörigkeit“ („1“) bzw. „Nicht-Zugehörigkeit“ („0“) sind die Kategorien der klassischen Mengenlehre. Die unscharfe Mengenlehre findet demgegenüber auch für Gegenstände, die – wie z. B. ein Drehstuhl oder ein Schaukelstuhl – nicht eindeutig als „Stuhl“ identifizierbar sind, eine mathematische Möglichkeit der Beschreibung: So hat ein Drehstuhl in Bezug auf die Kategorie „Stuhl“ nur eine Klassenzugehörigkeit von vielleicht 0.7 oder weniger.[13] Eine solche unscharfe Mengenlehre arbeitet also nicht nach dem sog. Bivalenzprinzip, das nur die Werte „0“ oder „1“ kennt.[14]

Jedem Element einer unscharfen Menge oder Teilmenge A kann also eine Zahl zwischen 0 und 1 („im Intervall [0,1]“) zugeordnet werden, die den Grad der Zugehörigkeit des Elements x zu dieser Menge repräsentiert. Genauer:

„Eine unscharfe Teilmenge (fuzzy subset) A einer Menge X ist gekennzeichnet durch ihre Zugehörigkeitsfunktion (membership function) μA: X → [ 0,1], die jedem Element x aus X eine Zahl μ A (x) im Intervall [0,1] zuordnet, die den Grad der Zugehörigkeit von x in A repräsentiert.“[15]

Damit kann eine kleine Teilmenge der unscharfen Menge „Stuhl“ folgendermaßen beschrieben werden:

A(Stuhl) = {(Küchenstuhl, 1), (Esszimmerstuhl, 1), (Drehstuhl, 0.7), (Schaukelstuhl, 0.5), (…)}.

Für unscharfe Relationen bei der Verknüpfung zweier unscharfer Mengen, also unscharfe Beziehungen zwischen zwei und mehreren Objekten, Sachverhalten, Größen usw., führt Adolf Grauel den Begriff der „Fuzzy-Relation“ ein.[16] Als Beispiel nennt er die „Farbe-Reifegrad-Relation“, die er in Form einer „Relationsmatrix zwischen Farbe x und Reifegrad y einer Frucht mit den möglichen Farben X ={grün, gelb, rot}und Reifegrade Y = {unreif, halbreif, reif}“ darstellt, die er folgendermaßen interpretiert: „WENN eine Frucht grün ist, DANN ist sie unreif. WENN eine Frucht gelb ist, DANN ist sie halbreif oder WENN eine Frucht rot ist, DANN ist sie reif.“[17] „Soll aber überdies noch formuliert werden, dass zu einem gewissen Prozentsatz eine grüne Frucht durchaus als halbreif angesehen werden kann, beispielsweise mit graduellen Zugehörigkeiten“, dann kann sich folgende Darstellung ergeben:

μ_R (grün,unreif)=1.0, μ_R (grün,halbreif)=0.5,

μ_R (grün,reif)=0.0, μ_R (gelb,unreif)=0.25,

μ_R (gelb,halbreif)=1.0, μ_R (gelb,reif)=0.25,

μ_R (rot,unreif)=0.0, μ_R (rot,halbreif)=0.5, und

μ_R (rot,reif)=1.0.[18]

Begriffe wie „grün“, „unreif“ „halbreif“ sind sog. linguistische Variablen, nach Hans-Jürgen Zimmermann wesentliche Elemente der Theorie der Fuzzy Sets. „Ihre Werte sind nicht – wie bei den üblichen numerischen Variablen – Zahlen, sondern Wörter und Ausdrücke (Terme) einer natürlichen Sprache. Da Wörter nicht so präzise wie Zahlen sind, werden sie durch unscharfe Mengen repräsentiert.“ Als Beispiel nennt er die Raumtemperatur, deren Werte einer Menge von Termen wie „kühl“, „angenehm“ oder „warm“ entspricht. Auch diese unscharf abgegrenzten Begriffe können mathematisch definiert werden. In der klassischen Theorie könnte dieser Bereich jedoch nur als scharf abgegrenztes Intervall, etwa von 19 bis 24 Grad Celsius, angegeben werden. „Dann würde jedoch beispielsweise eine Temperatur von 18,9 Grad als nicht angenehm eingestuft, was dem menschlichen Empfinden in dieser Form nicht entspricht. In unserem Beispiel würde man 18,9 Grad als 'vielleicht nicht mehr so angenehm' beurteilen, womit dieser Wert etwa mit dem Zugehörigkeitsgrad 0,8 der unscharfen Menge der angenehmen Raumtemperaturen angehören könnte.“[19] Als weitere Beispiele für sprachliche (lexikale) Unschärfe von Bedeutungen nennt Zimmermann Ausdrücke wie „großer Mann“, „heißer Tag“ oder „stabile Währung“. „Die Bedeutung dieser Wörter ergibt sich erst aus dem Zusammenhang, also aus der Person des Sprechers und dem Bezug, in dem der jeweilige Ausdruck benutzt wird.“[19]

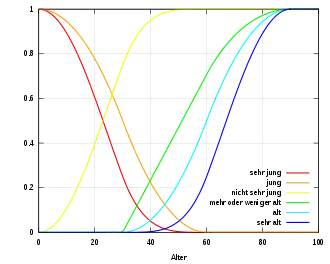
Fuzzyfunktion für das Alter eines Menschen

Ähnlich verhält es sich mit dem Alter von Menschen. In Jahren mag das Alter eines bestimmten Menschen zwar exakt angebbar sein; ob jedoch eine Zweiunddreißigjährige als „jung“ oder ein Vierundsechzigjähriger als „alt“ bezeichnet wird, hängt von vielen Faktoren ab, nicht zuletzt vom Alter des Beobachters. Das Alter eines „jungen“ oder „alten“ Menschen ist also nicht eindeutig definierbar, Begriffe wie „jung“ oder „alt“ sind unscharf. Graphisch lassen sich auch diese Verhältnisse als Fuzzy-Funktion mit Werten zwischen „0“ oder „1“ darstellen. Nach der nebenstehenden Abbildung[20], die allerdings nur für sog. „Standardsituationen“ gelten kann, also unabhängig von den spezifischen situativen und kontextuellen Gegebenheiten einer konkreten Situation, fällt zum Beispiel eine Zweiunddreißigjährige mit einem Zugehörigkeitsgrad von etwas unter 0,5 in die Kategorie „jung“, ein Vierundsechzigjähriger mit einem Zugehörigkeitsgrad von etwa 0,6 in die Kategorie „alt“.

Über solche Beschreibungen auf der Wortebene hinausgehend fordert Burghard Rieger (1998) generell die Entwicklung einer „Fuzzy Linguistik“, weil die Analyse konkreter sprachlicher Performanzdaten adäquat nur empirisch mit Hilfe unscharfer (Performanz-)Modellierungen erfolgen kann, nicht mit Hilfe traditioneller, d. h. kompetenztheoretischer scharfer Kategorien: „Die quantitative Beschreibung und numerische Analyse sprachlicher Elemente, Einheiten und Strukturen [mit aus Performanzdaten gewonnenen unscharfen Kategorien] bietet sich an, wenn es darum geht, Eigenschaften ihrer Verwendung, ihres Gebrauchs und der damit verbundenen Zusammenhänge zu ermitteln, die als (nicht unmittelbar beobachtbare) abgeleitete Funktionen ihres (beobachtbaren) Vorkommens beschrieben werden können. In Verbindung mit den fuzzy-theoretischen Möglichkeiten der Modellierung [KGK93] [Nov89] erlauben diese Verfahren die Definition von elastischen Einheiten [Zad75] – den soft constraints [Smo89b] in sub-symbolischen Modellen entsprechend – durch numerische Spezifizierungen und erhöhtes Auflösungsvermögen von Zugehörigkeitsgraden verbunden mit größeren Toleranzen der Kategorisierung und der Verarbeitung [Zad94]. … Unscharfe (fuzzy) Kategorien heißen dabei solche abstrakten Zuordnungen, deren (leere) Strukturen ebenso wie deren mögliche Füllungen als Resultate von Prozessen erscheinen, die in Form von Prozeduren dargestellt werden können.“[21]

So gesehen ist das Erkenntnisinteresse der „Fuzzy Linguistik … ein integratives, das sich auf eine Theorie der Performanz richtet. Dieser liegt aber nicht primär ein Vermögen zur Produktion korrekter Sätze zugrunde, sondern die kommunikative Kompetenz des sinnvollen Gebrauchs pragmatisch-funktionaler, d. h. bedeutsamer sprachlicher Äußerungen. Den Untersuchungsgegenstand bilden (verbale/schriftliche) Zeugnisse situierter sprachlicher Kommunikation, wobei die Untersuchungsmethoden alle Techniken der unscharfen (fuzzy) Modellierung umfassen, also auch solcher Verfahren, die von der Neueren Linguistik, Computerlinguistik und Quantitativen Linguistik eingesetzt werden.“[22]

Diese Problematik der pragmatisch-funktionalen Kontextabhängigkeit von Ausdrücken/Begriffen/Äußerungen hat seit den 1990er Jahren mehr und mehr zu einer Kritik an dem Erklärungs- und Beschreibungsansatz der Fuzzy-Set-Theorie geführt. Weitergehende Überlegungen traditioneller Ansätze[23] sprechen der Fuzzy-Set-Theorie sogar jegliche Erklärungsmöglichkeit für das Phänomen der sprachlichen Unschärfe ab und fokussieren stattdessen auf die Kontextabhängigkeit von Ausdrücken/Begriffen/Äußerungen.[24]

Siehe auch

Literaturverzeichnis

Hadumod Bußmann: Lexikon der Sprachwissenschaft (= Kröners Taschenausgabe. Band 452). 2., völlig neu bearbeitete Auflage. Kröner, Stuttgart 1990, ISBN 3-520-45202-2.
György Fuhrmann: m-Fuzziness in brain/mind modelling. In: Zétényi, 1988, S. 155–202.
Adolf Grauel: „Fuzzy Tutorial: Fuzzy-Logik in Theorie und Praxis“. Online hier (abgerufen am 15. März 2017).
Hannelore Grimm und Johannes Engelkamp: Sprachpsychologie. Handbuch und Lexikon der Psycholinguistik.Erich Schmidt Verlag, Berlin 1981.
Ingemund Gullvag und Arne Naess: Vagueness and ambiguity. In: Marcelo Dascal, Dietfried Gerhardus, Kuno Lorenz und Georg Meggle (Hrsg.): Sprachphilosophie. Philosophy of Language. La philosophie du langage. Ein internationales Handbuch zeitgenössischer Forschung. Zweiter Halbband, Berlin / New York: de Gruyter 1996, S. 1407–1417.
Rosanna Keefe und Peter Smith: Vagueness. A Reader. Cambridge: MIT Press, 1999, ISBN 0-262-61145-7.
Geert Keil: „Vagheit“. In: Markus Schrenk (Hrsg.): Handbuch Metaphysik. J.B. Metzler, Stuttgart 2017 (ISBN 978-3-476-05365-7), S. 121–127 (mit weiteren Nachweisen).
Theodor Lewandowski: Linguistisches Wörterbuch. 3 Bde. Heidelberg, Wiesbaden: Quelle & Meyer, 6. Aufl. 1994.
Martina Mangasser-Wahl: Prototypentheorie in der Linguistik: Anwendungsbeispiele, Methodenreflexion, Perspektiven. Tübingen: Stauffenburg 2000, ISBN 3-86057-706-9.
Klaus Mudersbach: „Begriffe in der Sicht des Sprachbenutzers“. In: Rudolf Wille (Hrsg.): Begriffliche Wissensverarbeitung: Grundfragen und Aufgaben. BI-Wiss.-Verl.: Mannheim [u. a.], 1994.
Ralf Pörings und Ulrich Schmitz (Hrsg.): Sprache und Sprachwissenschaft. Eine kognitiv orientierte Einführung. Tübingen: Narr, 1999 (ISBN 3-8233-4975-9). Online hier mit einem Link zum Download des Buches (abgerufen am 15. März 2017).
Burghard Rieger: „Theorie der unscharfen Mengen und empirische Textanalyse“ in: Wolfgang Klein (Hrsg.): Methoden der Textanalyse (= medium literatur 3), Heidelberg (Quelle & Meyer) 1977, S. 84–99. Online hier (zuletzt abgerufen am 8. Juli 2017).
Burghard Rieger: „Warum Fuzzy Linguistik? Überlegungen und Ansätze einer computerlinguistischen Neuorientierung“. In: Dieter Krallmann / H. Walter Schmitz (Hrsg.): Perspektiven einer Kommunikationswissenschaft. Vorträge des Internationalen Gerold-Ungeheuer-Symposium, Essen 1995. Bd. 1, Münster: Nodus 1998, ISBN 3-89323-651-1, S. 153–183. Online hier (zuletzt abgerufen am 15. April 2017).
Eleanor Rosch und Barbara B. Lloyd (Hrsg.): Cognition and categorization. Hillsdale, N.J. [u. a.]: Erlbaum, 1978, ISBN 0-470-26377-6.
Michael Smithson: „Possibility Theory, Fuzzy Logic, and Psychological Explanation“. In: Zétényi, 1988, S. 1–50.
Philipp Stoellger: „Vagheit“. In: Gert Ueding (Hrsg.): Historisches Wörterbuch der Rhetorik. Darmstadt: WBG, 1992ff., Bd. 10 (2011), Sp. 1364–1377.
Johannes-Peter Timm: „Die „Fuzziness“ der Sprache als Begründung für einen ganzheitlich-funktionalen, erfahrungsorientierten Grammatikunterricht“. In: Johannes-Peter Timm (Hrsg.): Ganzheitlicher Fremdsprachenunterricht. Deutscher Studien Verlag, Weinheim 1995, S. 120–148.
Wolfgang Wahlster: „Die Repräsentation von vagem Wissen in natürlichsprachlichen Systemen der Künstlichen Intelligenz“. Online hier (abgerufen am 12. März 2017).
Timothy Williamson: Vagueness. London: Routledge, 1994.
Lotfi Zadeh: „Fuzzy Sets“. Information and Control, 8, 1965, S. 338–353.
Tamás Zétényi (Hrsg.): Fuzzy sets in psychology. Amsterdam: North-Holland, 1988.
Hans-Jürgen Zimmermann: „Prinzipien der Fuzzy Logic“. Aus: Spektrum.de, 1. März 1993. Online hier (zuletzt abgerufen am 11. April 2017).

Weiterführende, online verfügbare Literatur

Geert Keil und Ralf Poscher (Projektleiter): Forschungsprojekt „Vernünftiger Umgang mit unscharfen Grenzen. Vagheits- und Unbestimmtheitsphänomene als Herausforderung für Philosophie und Recht“. Online hier; dazu umfangreiche Bibliographie: Online hier; umfangreicher Index: Online hier (alle zuletzt abgerufen am 15. Dezember 2018).
OTH Regensburg: „Fuzzy-Systeme“. Online hier (zuletzt abgerufen am 3. April 2017) (am 15. Dezember 2018 nur noch für angemeldete Benutzer verfügbar).
Burghard B. Rieger: „Unscharfe (fuzzy) Modellierung natürlichsprachiger Bedeutung. Zu einer computerlinguistischen Neuorientierung der Semantik“ (1998). Online hier (zuletzt abgerufen am 3. April 2017).
Roy Sorensen: Lemma „Vagueness“. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy. Online hier (abgerufen am 3. April 2017; seit 5. April 2018 stark überarbeitet).

Quellen

Wahlster: „Die Repräsentation von vagem Wissen “, S. 18.
Lewandowski: Linguistisches Wörterbuch 2. S. 538; s. v. Klassifikation.
Bußmann: Lexikon der Sprachwissenschaft …, S. 128.
Grimm und Engelkamp: Sprachpsychologie …, S. 190.
Mudersbach: „Begriffe ...“, S. 117.
Wie die Wikipedia-Einträge „Stuhl“ bzw. „Sessel“ zeigen, kann die Extension dieser Begriffe in verschiedenen Ländern (Deutschland, Österreich, Schweiz) allerdings durchaus unterschiedlich sein.
Timm: „Die 'Fuzziness' der Sprache …“, S. 123 f.
Lewandowski: Linguistisches Wörterbuch 1, S. 137; s. v. „Bedeutung“.
Sorites = „Häufelschluss“ zu sōròs „Haufen“: „Bezeichnung Ciceros für die auf Zeno zurückgehende Aporie: 'Bei welchem Wieviel beginnt der Haufen?'“ (nach: Duden. Das große Fremdwörterbuch. Herkunft und Bedeutung der Fremdwörter. 4., akt. Auflage, o. J. [2007], S. 1263.)
Fuhrmann: „m-Fuzziness ...“, S. 167 ff.
Pörings und Schmitz: Sprache und Sprachwissenschaft …, S. 19.
Rieger: Theorie der unscharfen Mengen und empirische Textanalyse. S. 84ff (online)
„Aufgrund der Willkür bei der Wahl dieser Funktion stellt die Fuzzy-Mengentheorie eine sehr subjektive Methode dar, die sich daher besonders zur Repräsentation von menschlichem Wissen eignet.“ (nach: Informationsfusion#Fuzzy-Logik, abgerufen am 19. April 2017) - Solche Ausprägungen zwischen „0“ und „1“, die von einem Sprecher des Deutschen zum andern variieren können, bedürfen natürlich einer empirischen Überprüfung anhand einer größeren Stichprobe.
Vgl. auch Unschärfe#Logik und Sprachtheorie
Grauel: „Fuzzy Tutorial …“, S. 14.
Grauel: „Fuzzy Tutorial …“, S. 60.
Grauel: „Fuzzy Tutorial …“, S. 62.
Grauel: „Fuzzy Tutorial ...“, S. 63.
Zimmermann: „Prinzipien der Fuzzy Logic“ (online).
Abbildung übernommen aus: Beispiel für eine nicht-lineare Fuzzy-Funktion; abgerufen am 6. Mai 2017.
Rieger: „Warum Fuzzy Linguistik?“, S. 14.
Rieger: „Warum Fuzzy Linguistik?“, S. 24.
Uli Sauerland: Vagueness in Language: The Case Against Fuzzy Logic Revisited. In P. Cintula, C. Fermüller, L. Godo, P. Hájek (Hrsg.): Understanding Vagueness – Logical, Philosophical, and Linguistic Perspectives. (Studies in Logic 36), College Publications, London 2011, S. 185–198.
Vgl. Fuzzylogik#Fuzzy-Set-Theorie.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Wahlster: „Die Repräsentation von vagem Wissen “, S. 18.

[2] Lewandowski: Linguistisches Wörterbuch 2. S. 538; s. v. Klassifikation.

[3] Bußmann: Lexikon der Sprachwissenschaft …, S. 128.

[4] Grimm und Engelkamp: Sprachpsychologie …, S. 190.

[5] Mudersbach: „Begriffe ...“, S. 117.

[6] Wie die Wikipedia-Einträge „Stuhl“ bzw. „Sessel“ zeigen, kann die Extension dieser Begriffe in verschiedenen Ländern (Deutschland, Österreich, Schweiz) allerdings durchaus unterschiedlich sein.

[7] Timm: „Die 'Fuzziness' der Sprache …“, S. 123 f.

[8] Lewandowski: Linguistisches Wörterbuch 1, S. 137; s. v. „Bedeutung“.

[9] Sorites = „Häufelschluss“ zu sōròs „Haufen“: „Bezeichnung Ciceros für die auf Zeno zurückgehende Aporie: 'Bei welchem Wieviel beginnt der Haufen?'“ (nach: Duden. Das große Fremdwörterbuch. Herkunft und Bedeutung der Fremdwörter. 4., akt. Auflage, o. J. [2007], S. 1263.)

[10] Fuhrmann: „m-Fuzziness ...“, S. 167 ff.

[11] Pörings und Schmitz: Sprache und Sprachwissenschaft …, S. 19.

[12] Rieger: Theorie der unscharfen Mengen und empirische Textanalyse. S. 84ff (online)

[13] „Aufgrund der Willkür bei der Wahl dieser Funktion stellt die Fuzzy-Mengentheorie eine sehr subjektive Methode dar, die sich daher besonders zur Repräsentation von menschlichem Wissen eignet.“ (nach: Informationsfusion#Fuzzy-Logik, abgerufen am 19. April 2017) - Solche Ausprägungen zwischen „0“ und „1“, die von einem Sprecher des Deutschen zum andern variieren können, bedürfen natürlich einer empirischen Überprüfung anhand einer größeren Stichprobe.

[14] Vgl. auch Unschärfe#Logik und Sprachtheorie

[15] Grauel: „Fuzzy Tutorial …“, S. 14.

[16] Grauel: „Fuzzy Tutorial …“, S. 60.

[17] Grauel: „Fuzzy Tutorial …“, S. 62.

[18] Grauel: „Fuzzy Tutorial ...“, S. 63.

[ReferenceA-19] Zimmermann: „Prinzipien der Fuzzy Logic“ (online).

[20] Abbildung übernommen aus: Beispiel für eine nicht-lineare Fuzzy-Funktion; abgerufen am 6. Mai 2017.

[21] Rieger: „Warum Fuzzy Linguistik?“, S. 14.

[22] Rieger: „Warum Fuzzy Linguistik?“, S. 24.

[23] Uli Sauerland: Vagueness in Language: The Case Against Fuzzy Logic Revisited. In P. Cintula, C. Fermüller, L. Godo, P. Hájek (Hrsg.): Understanding Vagueness – Logical, Philosophical, and Linguistic Perspectives. (Studies in Logic 36), College Publications, London 2011, S. 185–198.

[24] Vgl. Fuzzylogik#Fuzzy-Set-Theorie.