T-Dualität

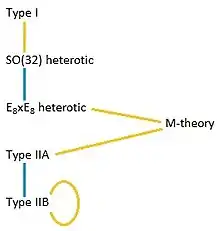
Die T-Dualität ist in der Elementarteilchenphysik eine Beziehung zwischen verschiedenen Superstringtheorien bzw. allgemeiner Quantenfeldtheorien, die besagt dass sie im Wesentlichen das gleiche physikalische Modell beschreiben. Das eine Modell ist dual zum anderen. Der Nachweis der T-Dualität bestimmter Superstringtheorien hat maßgeblich zur Entwicklung der M-Theorie beigetragen. Durch die T-Dualität ergibt sich beispielsweise, dass die Typ II-Superstringtheorie (Typ IIA und Typ IIB) dieselbe Theorie beschreiben (Edward Witten, 1995) und ebenso die beiden heterotischen Superstringtheorien mit Eichgruppen E8 x E8 und SO(32).[1][2]

Dieser Artikel wurde in die Qualitätssicherung der Redaktion Physik eingetragen. Wenn du dich mit dem Thema auskennst, bist du herzlich eingeladen, dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der Meinungsaustausch darüber findet derzeit nicht auf der Artikeldiskussionsseite, sondern auf der Qualitätssicherungs-Seite der Physik statt.

Verknüpfungen zwischen Stringtheorien S-dual (gelb) und T-dual (blau)

Das T steht für englisch target space und kommt daher, dass die zugrundeliegenden Raum-Zeit-Geometrien verschieden sind. Neben der T-Dualität gibt es noch weitere Dualitäten in der Stringtheorie wie die S-Dualität.

Die T-Dualität hat Verbindungen zur Spiegelsymmetrie (Mirror Symmetry) zwischen Calabi-Yau-Mannigfaltigkeiten. In der Superstringtheorie ergeben sich aus der Kompaktifizierung der in zehn Raum-Zeit-Dimensionen formulierten Superstringtheorie auf die vier Raum-Zeit-Dimensionen unseres Universums kompakte sechsdimensionale Calabi-Yau-Mannigfaltigkeiten für die Extradimensionen. Die häufig hypothetischen Spiegelsymmetrien verbinden verschiedene Calabi-Yau-Mannigfaltigkeiten, so dass diese die gleiche physikalische Theorie beschreiben ähnlich wie bei der T-Dualität.

Die T-Dualität verbindet im einfachsten Fall Stringtheorien in Raum-Zeiten, deren kompaktifizierte Dimensionen einem Kreis mit dem Radius R in der einen Theorie und dem reziproken Radius 1/R in der anderen, dualen Theorie. Beim Übergang zum dualen Modell werden die Windungsmoden und Schwingungsmoden der Strings vertauscht. Die diskretisierten Impulse der Schwingungsmoden entsprechen den Windungszahlen der Strings im kompaktifizierten Raum des dualen Modells.

Dass zwei (Super-)Stringtheorien zueinander unter Umständen T-dual oder S-dual sein können, veranlasste Witten 1995 zu der Annahme, dass sämtliche Stringtheorien sowie die Supergravitation nur ein Teil einer größeren, allumfassenderen Theorie sind, die er M-Theorie nannte.

Einzelnachweise

Edward Witten: Five-branes and M-Theory On An Orbifold. In: Nuclear Physics B. Band 463, Nr. 3, Januar 1996, S. 383–397, doi:10.1016/0550-3213(96)00032-6, arxiv:hep-th/9512219v1.
John H. Schwarz: The Power of M Theory. In: Nuclear Physics B. Band 367, Nr. 1-4, Oktober 1995, S. 97–103, doi:10.1016/0370-2693(95)01429-2, arxiv:hep-th/9510086v1.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Edward Witten: Five-branes and M-Theory On An Orbifold. In: Nuclear Physics B. Band 463, Nr. 3, Januar 1996, S. 383–397, doi:10.1016/0550-3213(96)00032-6, arxiv:hep-th/9512219v1.

[2] John H. Schwarz: The Power of M Theory. In: Nuclear Physics B. Band 367, Nr. 1-4, Oktober 1995, S. 97–103, doi:10.1016/0370-2693(95)01429-2, arxiv:hep-th/9510086v1.